A particle of mass m, moving in a circle of radius R, has a velocity v=v0(1−e−γt) The power delivered to tha particle by the force at t=0 is
To find the power delivered to a particle of mass m moving in a circle of radius R with a velocity given by v=v0(1−e−γt) at t=0, we can follow these steps:
Step 1: Understand the formula for power
Power P delivered to the particle by the force is given by the formula:
P=F⋅v
where F is the force acting on the particle and v is its velocity.
Step 2: Determine the force acting on the particle
The force F can also be expressed in terms of mass m and acceleration a:
F=m⋅a
To find the acceleration, we need to differentiate the velocity function with respect to time.
Step 3: Differentiate the velocity to find acceleration
The velocity is given as:
v=v0(1−e−γt)
Differentiating this with respect to t:
a=dvdt=v0⋅ddt(1−e−γt)=v0⋅γe−γt
Step 4: Calculate acceleration at t=0
Now, substituting t=0 into the acceleration equation:
a(0)=v0⋅γe0=v0⋅γ
Step 5: Substitute acceleration into the force equation
Now substitute the acceleration back into the force equation:
F=m⋅a=m⋅(v0⋅γ)
Step 6: Calculate velocity at t=0
Next, we calculate the velocity at t=0:
v(0)=v0(1−e0)=v0(1−1)=0
Step 7: Calculate power at t=0
Now we can find the power at t=0:
P(0)=F⋅v(0)=(m⋅v0⋅γ)⋅0=0
Final Answer
Thus, the power delivered to the particle by the force at t=0 is:
0
---
Power P delivered to the particle by the force is given by the formula:
P=F⋅v
where F is the force acting on the particle and v is its velocity.
The force F can also be expressed in terms of mass m and acceleration a:
F=m⋅a
To find the acceleration, we need to differentiate the velocity function with respect to time.
The velocity is given as:
v=v0(1−e−γt)
Differentiating this with respect to t:
a=dvdt=v0⋅ddt(1−e−γt)=v0⋅γe−γt
Now, substituting t=0 into the acceleration equation:
a(0)=v0⋅γe0=v0⋅γ
Now substitute the acceleration back into the force equation:
F=m⋅a=m⋅(v0⋅γ)
Next, we calculate the velocity at t=0:
v(0)=v0(1−e0)=v0(1−1)=0
Now we can find the power at t=0:
P(0)=F⋅v(0)=(m⋅v0⋅γ)⋅0=0
Thus, the power delivered to the particle by the force at t=0 is:
0
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - More than One Option is Correct
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Comprehension
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Main
23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
If a particle of mass m is moving in a horizontal circle of radius r with a centripetal force (−1/r2) , the total energy is
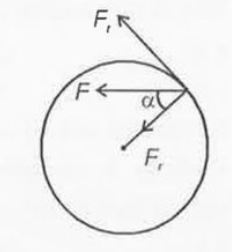
View SolutionA particle of mass m is moving in a circle of radius (r) with changing speed (v) the direction of centripetal force and tangential force are shown below the value of α is
View SolutionA particle of mass M is moving in a circle of fixed radius R in such a way that its centripetal acceleration at time t is given by n2Rt2 where n is a constant. The power delivered to the particle by the force acting on it, it :
View SolutionA particle is moving on a circular path of radius 1 m with 2 m/s. If speed starts increasing at a rate of 2m/s2, then acceleration of particle is
View SolutionA particle of mass m is projected upword with velocity v=ve2 (ve) escape of the particle is
View SolutionA particle of mass m moves along a horizontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Tangential force on particle at t s is
View SolutionA particle of mass m moves along a horizontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Total force on particle at time t s is
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionA particle is moving in a circle of radius R with constant speed. The time period of the particle is T. In a time t=T6
Average velocity of the particle is…..
View SolutionIf a particle moves in a circle of radius of 4m at speed given by v=2t where v is in m/s and t in sec.At t=4s ,net accleration of particle will be:
View Solution
