A particle P is moving in a circle of radius a with a uniform speed u, C is the centre of the circle and AB is a diameter. The angular velocities of P about A and C are in the ratio
A
1:1
B
1:2
C
2:1
D
4:1
Text Solution
The correct Answer is:B
From the property of a circle, if an arc subtend an angle θ at any point A on circumference, then it will subtend an angle 2θ at centre C. So in the same time interval a particle rotating in a circle turn double the angle with respect to centre point C compared to point A.
∴ωc=2ωA.
|
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Knowledge Check
A particle P is moving in a circle of radius r with a uniform speed u. C is the centre of the circle and AB is diameter. The angular velocity of P about A and V are in the ratio :
A1:2B2:1C1:3D3:1A particle 'P' is moving in a circle of radius 'a' with a uniform speed 'u' 'C' is the centre of the circle and AB is a diameter. The angular velocity of P about A and C are in the ratio
A1:1B1:2C2:1D4:1A particle P is moving in a circle of radius r with a uniform speed u. C is the centre of the circle and AB is diameter. The angular velocity of P about A and C are in the ratio :

A1:1B1:2C2:1D4:1
In the figure , point P is the centre of the circle and AB is the diameter . The co-ordinates of A are
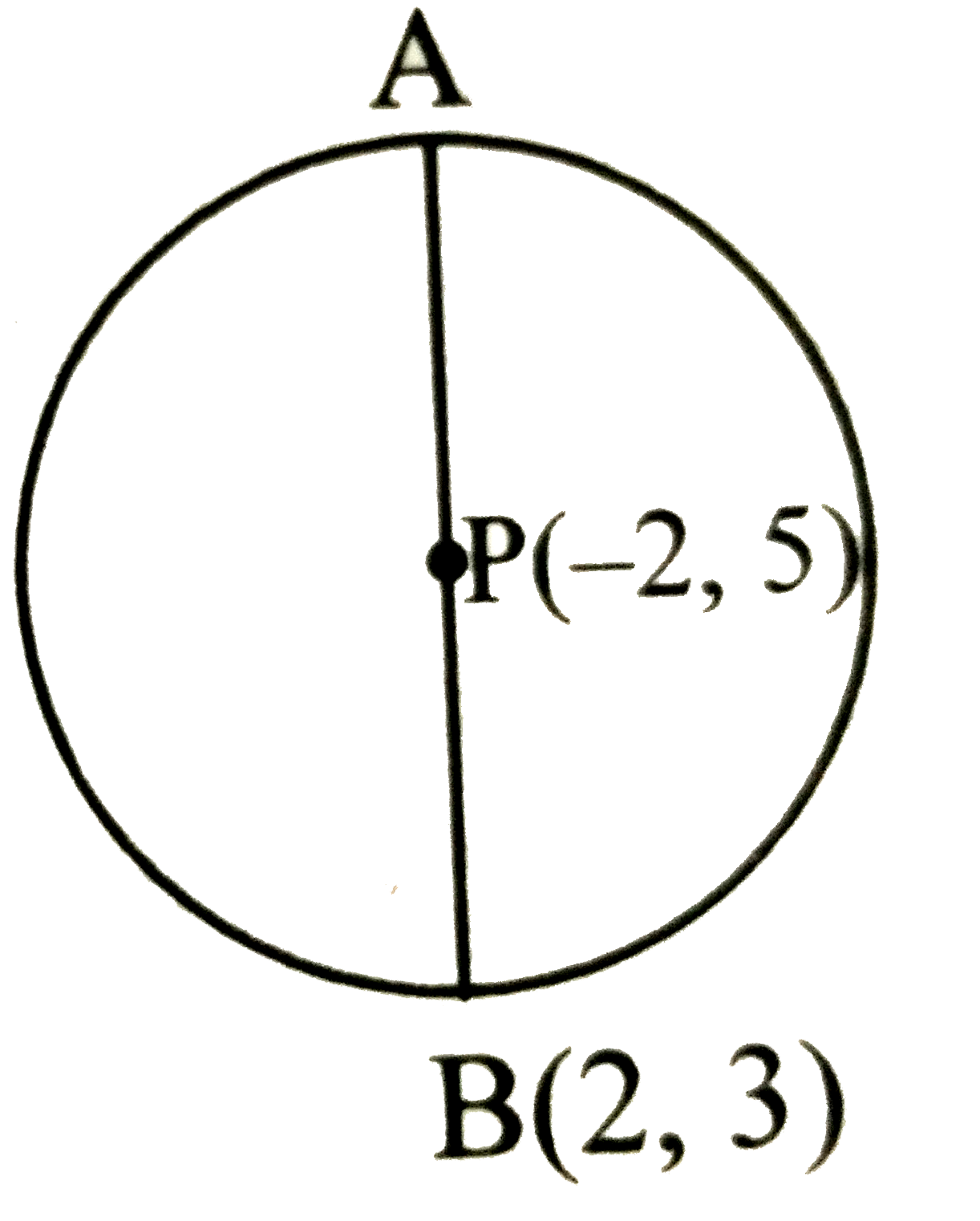
View SolutionWhen a particle moves in a circle with a uniform speed
View SolutionA particle is moving in a circle with uniform speed. IT has constant
View SolutionWhen a particle moves in a circle with a uniform speed
View SolutionA particle moves in a circle of radius 20 cm with linear speed of 10 m/s. Find the angular velocity
View Solution
