A particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of displacement (a) in successive second and (b) in successive time interval t0.
(i) Displacement in 1 s or 1st second
s1=ut+12at2=0+12a(1)2=12a
or s1=u+12a(2t−1)=0+12a(2×1−1)=12a
Displacement in the 2nd second
s2=u+12a(2t−1)=0+12a(2×2−1)=32a
Displacement in the 3rd second
s3=0+12a(2×3−1)=53a
s1:s2:s3:...=12a:32a:52a:...=1:3:5:....
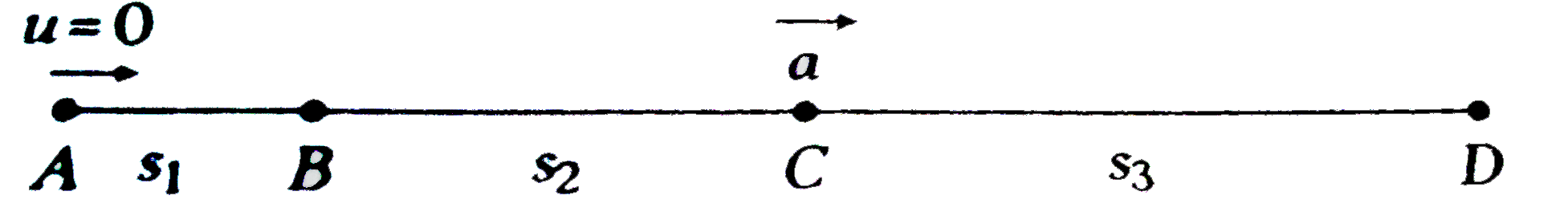
A to B : Displacement in the first t0 second
s=ut+12at2⇒s1=0+12at20=12at20
A to C t=t0+t0=2t0
s1+s2=0+12a(t0+t0)2=412at20
Displacement in the next t0 second
s2=32at20
A to D t=t0+t0+t0=3t0
s1+s2+s3=0+12a(t0+t0+t0)2=92at20
Displacement in the next t0 second
s3=52at20⇒s1:s2:s3=1:3:5
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.1
10 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.2
10 Videos
- MOTIONBOOK - DC PANDEYCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
A particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of time in successive displacement d.
View SolutionA partical is moving in a straight line under constant acceletation. If the motion starts from rest, Find the ratio of displacement in n second to that in the nth second.
View Solution
Knowledge Check
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A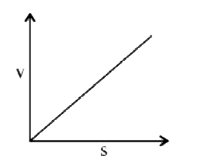 B
B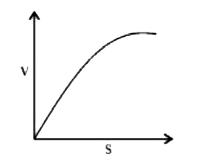 C
C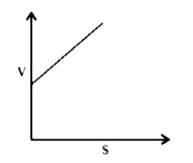 D
D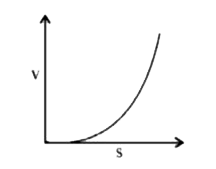
A particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
A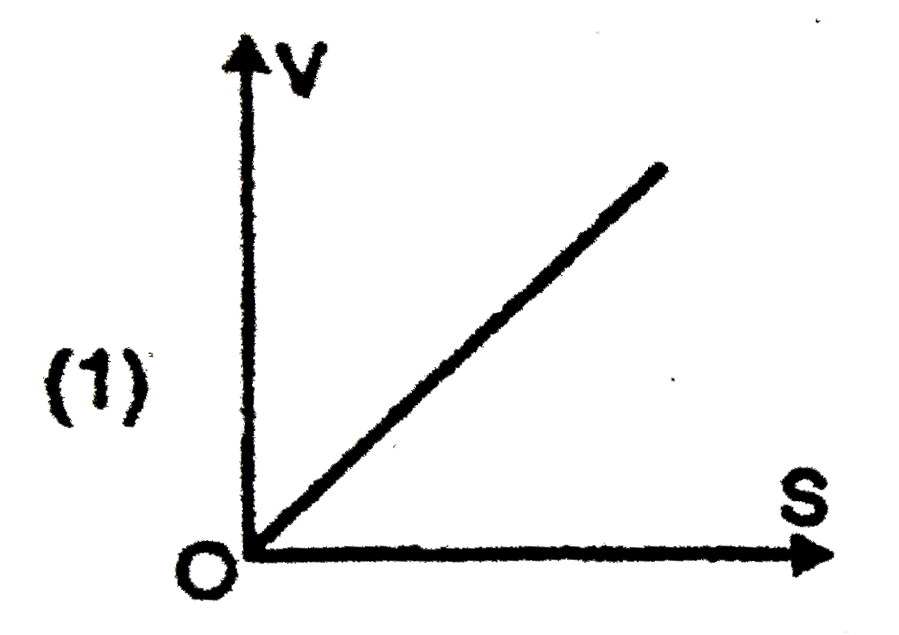 B
B C
C D
D
A body starts from rest and moves with constant acceleration. The ratio of distance covered by the body in nth second to that covered in n second is.
A1nB2n−1n2Cn22n−1D2n−12n2
A wheel rotates under constant angular acceleration starting from rest. Find the ratio of angle rotated in nsecond and nthsecond.
View SolutionA particle starts from rest at t=0 and undergoes an acceleration as shown in figure.
Draw the displacement-time graph of the motion of the particle during the same time interval. In both the above cases, explain the various steps.
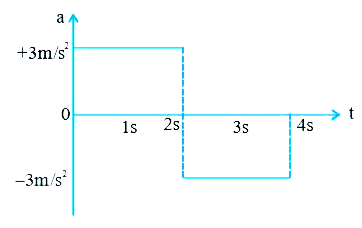
View SolutionA particle starts moving from position of rest under a constant acceleration if it travels a distance x in t second, what distance will it travel in next t second?
View SolutionA particle, starting from rest, moves in a straight line with constant acceleration a0 for a time interval t0.Then is accelerates at a constant rate 2a0 for time interval 2t0 .The distance travelled by the particle in time 3t0 from the starts is S . Then Sa0t20=
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is

View Solution
