A plank of mass 5kg is placed on a frictionless horizontal plane. Further a block of mass 1kg is placed over the plank. A massless spring of natural length 2m is fixed to the plank by its one end. The other end of spring is compressed by the block by half of spring's natural length. They system is now released from the rest. What is the velocity of the plank when block leaves the plank? (The stiffness constant of spring is 100N/m)

The correct Answer is:A, C
Let the velocity of the block and the plank, when the block leaves the spring be u and v respectivley.
By conservation of energy 12kx2=12mu2+12Mv2
[M=mass of the plank, m=mass of the block]
∴100=u2+5v2 …(i)
By conservation of momentum
mu+Mv=0
⇒u=−5y ...(ii)
Solving Eqs. (i) and (ii)
30v2=100⇒∴v=√103m/s
From this moment until block falls, both plank and block keep their velocity constant.
Thus, when block falls velocity of plank
=√103m/s
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Comprehension Based Questions
3 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Find the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionA block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
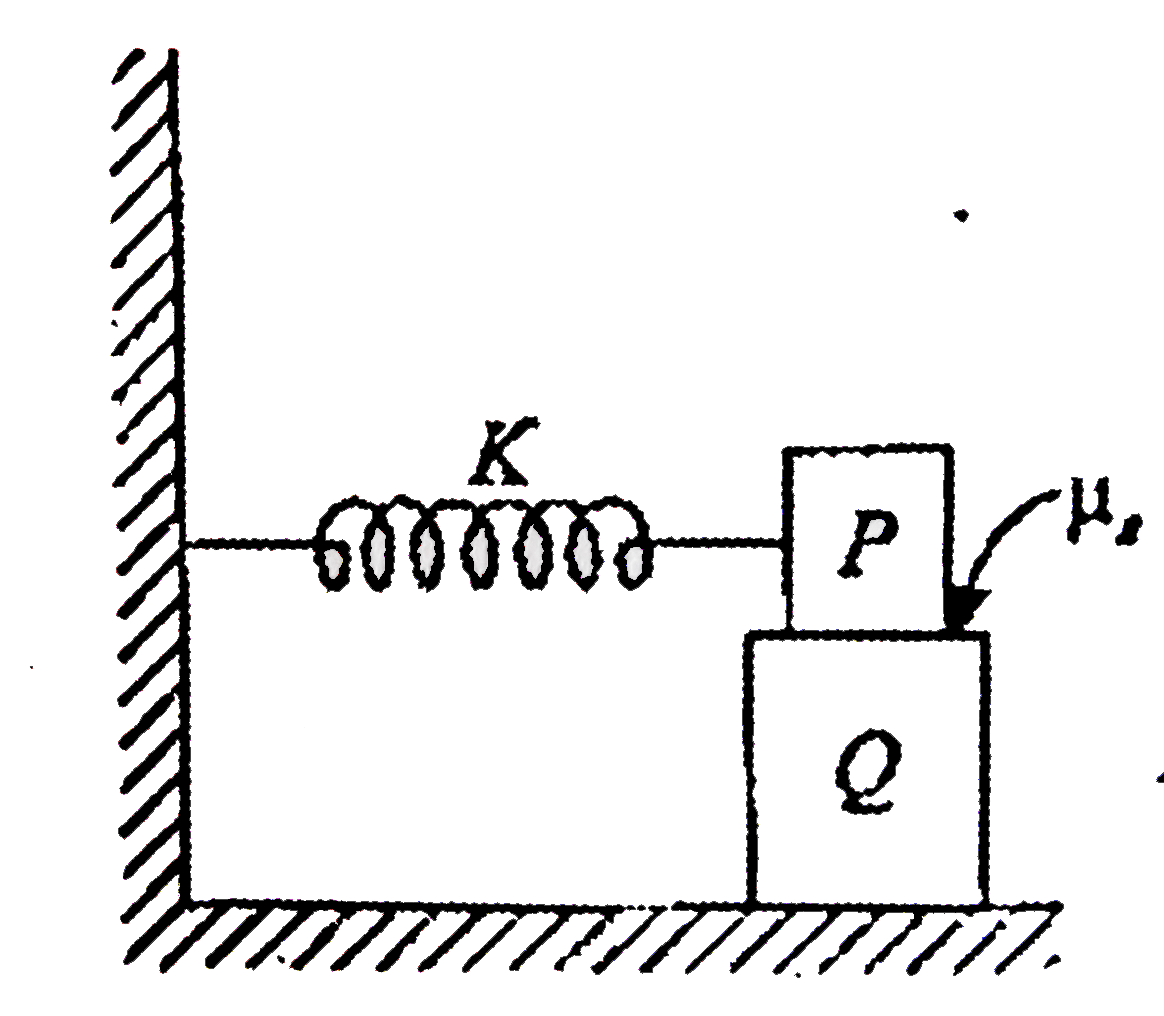
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

View SolutionA block of mass m is pushed against a spring of spring constant k fixed at the end to a wall. The block can side on a frictionless table as shown in figure. The natural length of the spring is L0 and it is compressed ti half its natural length when the block is relesed. Find teh velocity of the block aa s function of its distance x from the wall .

View SolutionA plank of mass 2kg and length 1m is placed on horizontal floor.A small block of mass 1kg is placed on top of the plank , at its right extreme end .The coefficient of friction between plank and floor is 0.5 and that between plank and block is 0.2 . If a horizontal force =30N starts acting on the plank to the right ,the time after which the block will fall off the plank is (g=10ms−2)
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
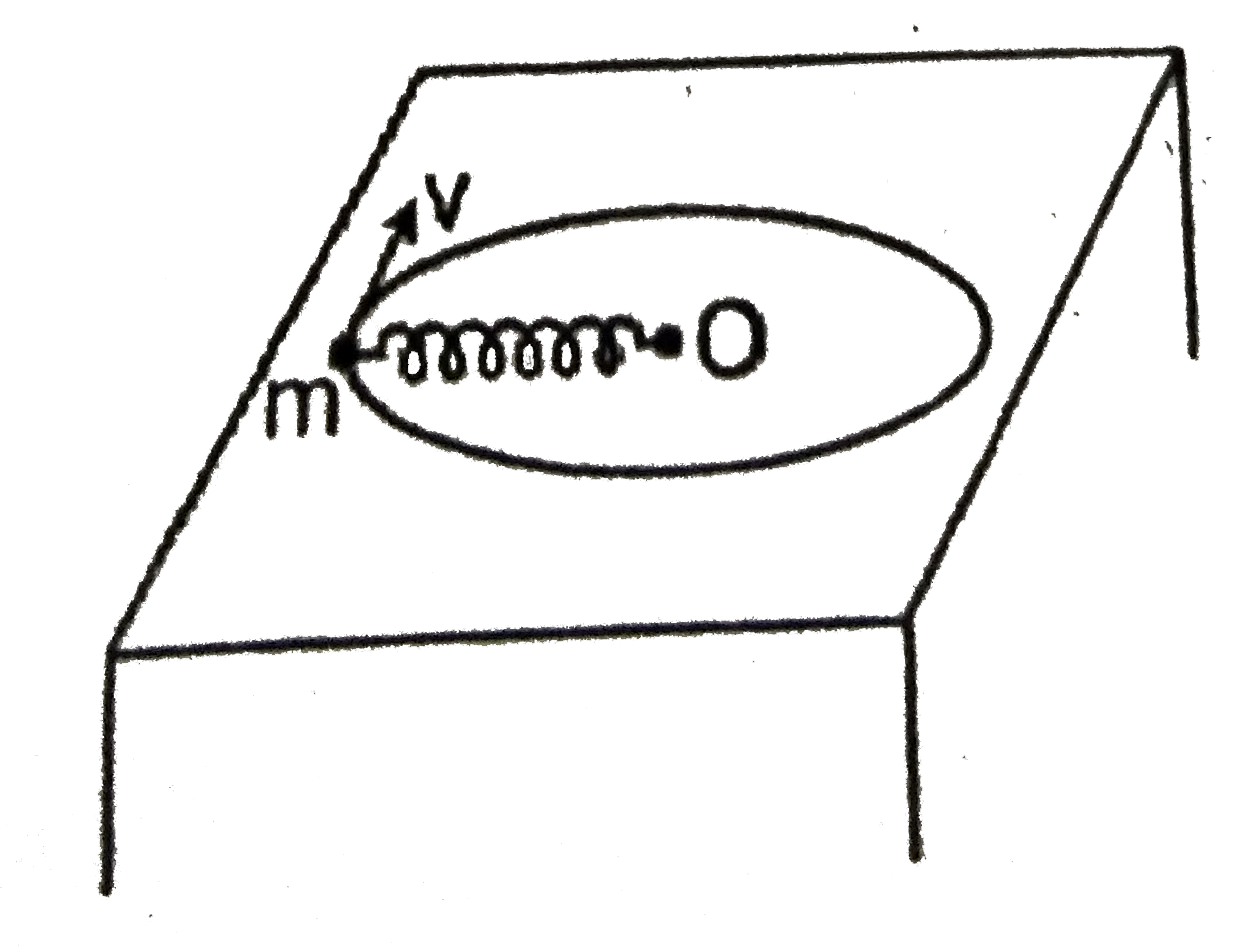
View SolutionMass m is connected with an ideal spring of natural length l whose other end is fixed on a smooth horizontal table. Initially spring is in its natural length l. Mass m is given a velocity 'v' perpendicular to the spring and released . The velocity perpendicular to the spring when its length l+x , will be
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View Solution
