A radioactive nucleus can decay by two differnet processess. The mean value period for the first process is t1 and that the second process is t2 .The effective mean value period for the two processes is .
t1+t22
t1+t2
√t1t2
t1+t2t1+t2
The correct Answer is:d
To find the effective mean value period for a radioactive nucleus that can decay by two different processes, we can follow these steps:
Step 1: Understand the decay processes
We have two decay processes characterized by their mean value periods:
- For the first process, the mean value period is T1.
- For the second process, the mean value period is T2.
Step 2: Relate mean value periods to decay constants
The decay constant (λ) is related to the mean value period (T) by the formula:
λ=1T
Thus, we can express the decay constants for both processes:
- For the first process:
λ1=1T1
- For the second process:
λ2=1T2
Step 3: Write the equation for the total decay rate
The total decay rate (dndt) for the nucleus can be expressed as:
dndt=−λ1n−λ2n
This can be rewritten as:
dndt=−(λ1+λ2)n
Step 4: Substitute the decay constants
Substituting the expressions for λ1 and λ2:
dndt=−(1T1+1T2)n
Step 5: Find the effective decay constant
The effective decay constant (λeffective) can be defined as:
λeffective=λ1+λ2=1T1+1T2
Step 6: Relate effective decay constant to effective mean value period
The effective mean value period (Teffective) is related to the effective decay constant by:
λeffective=1Teffective
Thus, we can express Teffective as:
Teffective=1λeffective=1(1T1+1T2)
Step 7: Simplify the expression
To simplify the expression for Teffective:
Teffective=1(1T1+1T2)=T1T2T1+T2
Final Result
The effective mean value period for the two processes is:
Teffective=T1T2T1+T2
We have two decay processes characterized by their mean value periods:
- For the first process, the mean value period is T1.
- For the second process, the mean value period is T2.
The decay constant (λ) is related to the mean value period (T) by the formula:
λ=1T
Thus, we can express the decay constants for both processes:
- For the first process:
λ1=1T1
- For the second process:
λ2=1T2
The total decay rate (dndt) for the nucleus can be expressed as:
dndt=−λ1n−λ2n
This can be rewritten as:
dndt=−(λ1+λ2)n
Substituting the expressions for λ1 and λ2:
dndt=−(1T1+1T2)n
The effective decay constant (λeffective) can be defined as:
λeffective=λ1+λ2=1T1+1T2
The effective mean value period (Teffective) is related to the effective decay constant by:
λeffective=1Teffective
Thus, we can express Teffective as:
Teffective=1λeffective=1(1T1+1T2)
To simplify the expression for Teffective:
Teffective=1(1T1+1T2)=T1T2T1+T2
The effective mean value period for the two processes is:
Teffective=T1T2T1+T2
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Linked Comprehension
29 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Integer
6 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Subjective
35 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer Type
4 Videos
Similar Questions
A radioactive nucleus can decay by two different processes. The half-life for the first process is t1 and that for the second process is t2. Show that the effective half-life t of the nucleus is given by
1t=1t1+1t2.
View SolutionA radioactive nucleus decays by two different processes. The half life for the first process is 10 s and that for the second is 100 s. The effective half life of the nucleus is close to :
View SolutionA radioactive nucleus can decay by three different processes. Half life for first process is 2 hours . Effective half life of the necleus is 43 hours. Find the half for second process in hours.
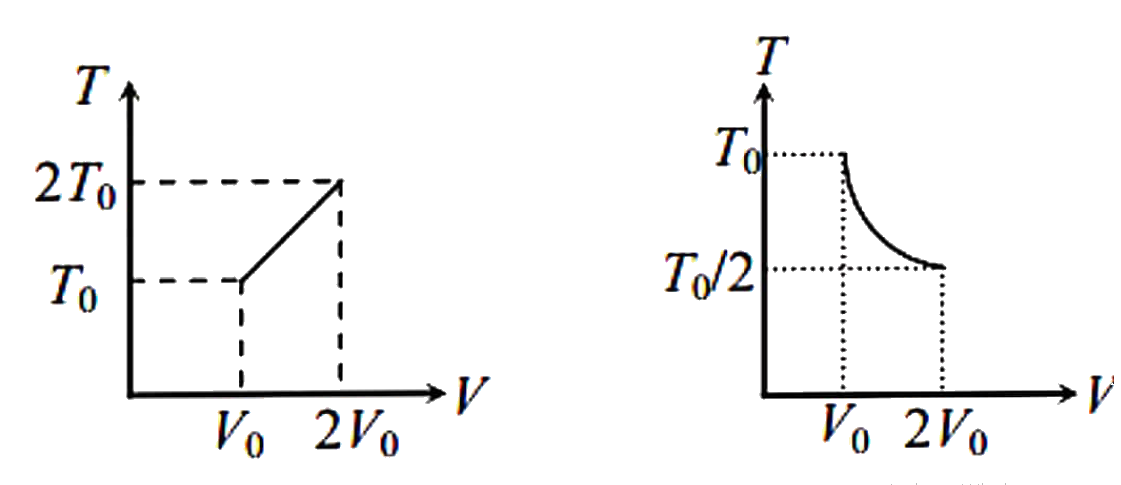
View SolutionTemperature and volume curves are drawn for two thermodynamic processes. For the first process, it is a straight line and for the second, it is a rectangular hyperbola. The ratio of work done in the first process to the work done in the second process is
View SolutionA system undergoes two cyclic process 1 and 2. Process 1 is reversible and process 2 is irreversible. The correct statement relating to the two processes is
View SolutionAn ideal gaseous sample at initial state I (P0,V0,T0) is allowed to expand to volume 2V0 using two different process, in the first process the equation of process is PV2=K1 and in second process the equation of the process is PV=K2.Then
View SolutionA radioactive sample decays through two different decay processes α-decay and β-decay. Half-life time for α−decay is 3h and half-life time for β−decay is 6h. What will be the ratio of number of initial radioactive to the number of nuclei present after 6h?.
View SolutionA sample of radioactive material decays simultaneouly by two processes A and B with half-lives 12 and 14h, respectively. For the first half hour it decays with the process A, next one hour with the proecess B, and for further half an hour with both A and B. If, origianlly, there were N0 nuceli, find the number of nuclei after 2 h of such decay.
View SolutionA sample of radioactive material decays simultaneouly by two processes A and B with half-lives 12 and 14h, respectively. For the first half hour it decays with the process A, next one hour with the proecess B, and for further half an hour with both A and B. If, origianlly, there were N0 nuceli, find the number of nuclei after 2 h of such decay.
View SolutionA mass is suspended separately by two different springs in successive order then time period is t1 and t2 respectively. If it is connected by both spring as shown in figure then time period is t0, the correct relation is : -

View Solution
