A ray of light travelling in glass (μg=3/2) is incident on a horizontal glass-air surface at the critical angle θC. If a thin layer of water (μw=4/3) is now poured on the glass-air surface. At what angle will the ray of light emerges into water at glass-water surface?
The correct Answer is:A, C, D
To solve the problem step by step, we will use Snell's Law and the concept of critical angle.
Step 1: Understand the Critical Angle
The critical angle θC is the angle of incidence in the denser medium (glass) at which the angle of refraction in the less dense medium (air) is 90∘. This can be expressed using Snell's Law:
μgsin(θC)=μairsin(90∘)
Given that μair=1 (the refractive index of air), we can simplify this to:
μgsin(θC)=1
Step 2: Calculate the Critical Angle
We know the refractive index of glass μg=32. Thus, we can find the critical angle θC:
32sin(θC)=1⟹sin(θC)=23
Now, we can find θC using the inverse sine function:
θC=sin−1(23)
Step 3: Introduce Water Layer
Now, when a thin layer of water (with refractive index μw=43) is poured on the glass-air surface, we need to find the angle at which the ray of light emerges into water at the glass-water surface.
Step 4: Apply Snell's Law at Glass-Water Interface
At the glass-water interface, we can use Snell's Law again:
μgsin(θC)=μwsin(θ1)
Where θ1 is the angle of refraction in water. Since we already established that μgsin(θC)=1:
1=μwsin(θ1)⟹sin(θ1)=1μw=143=34
Step 5: Calculate Angle θ1
Now, we can find θ1:
θ1=sin−1(34)
Step 6: Apply Snell's Law at Water-Air Interface
Next, we need to find the angle θ2 at which the ray of light emerges into the air from water. Applying Snell's Law again:
μwsin(θ1)=μairsin(θ2)
Since μair=1:
μwsin(θ1)=sin(θ2)
Substituting μw=43 and sin(θ1)=34:
43⋅34=sin(θ2)⟹sin(θ2)=1
Thus, θ2=90∘.
Conclusion
The angle at which the ray of light emerges into the water at the glass-water surface is 90∘.
---
The critical angle θC is the angle of incidence in the denser medium (glass) at which the angle of refraction in the less dense medium (air) is 90∘. This can be expressed using Snell's Law:
μgsin(θC)=μairsin(90∘)
Given that μair=1 (the refractive index of air), we can simplify this to:
μgsin(θC)=1
We know the refractive index of glass μg=32. Thus, we can find the critical angle θC:
32sin(θC)=1⟹sin(θC)=23
Now, we can find θC using the inverse sine function:
θC=sin−1(23)
Now, when a thin layer of water (with refractive index μw=43) is poured on the glass-air surface, we need to find the angle at which the ray of light emerges into water at the glass-water surface.
At the glass-water interface, we can use Snell's Law again:
μgsin(θC)=μwsin(θ1)
Where θ1 is the angle of refraction in water. Since we already established that μgsin(θC)=1:
1=μwsin(θ1)⟹sin(θ1)=1μw=143=34
Now, we can find θ1:
θ1=sin−1(34)
Next, we need to find the angle θ2 at which the ray of light emerges into the air from water. Applying Snell's Law again:
μwsin(θ1)=μairsin(θ2)
Since μair=1:
μwsin(θ1)=sin(θ2)
Substituting μw=43 and sin(θ1)=34:
43⋅34=sin(θ2)⟹sin(θ2)=1
Thus, θ2=90∘.
The angle at which the ray of light emerges into the water at the glass-water surface is 90∘.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions8videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Single Correct41videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions1videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
A ray of light travelling in glass (μ=3/2) is incident on a horizontal glass air surface at the critical angle θC. If a thin layer of water (μ=4/3) is now poured on the glass air surface, the ray of light emerge into air at the water air surface at an angle of π/k, radians find the value of k.
View SolutionA ray of light travelling obliquely from glass to air :
View SolutionA ray of light travelling in glass having refractive index _(a)μg=3/2 is incident at a critical angle C on the glass air interface. If a thin layer of water is poured on glass air interface, then what will be the angle of emergence of this ray in air when it emerges from water air inteface?
View SolutionA ray of ordinary light is travelling in air. It is incident on air glass pair at a polarising angle of 56∘. Find the angle of refraction in glass.
View SolutionA ray of light travelling in water is incident on its surface open to air. The angle of incidence is θ, which is less than the critical angle. Then there will be
View SolutionOrdinary light is incident on the upper surface of a glass slab at theh polarizing angle. Then
View Solution
A ray of light is incident at the glass-water interface at an angle i it emerges finnaly parallel to the surface of water, then the value of μg would beView SolutionWhen light travels from glass to air, the incident angle is θ1 and the refracted angle is θ2. The true relation is
View SolutionA ray of light strikes a glass slab (R.l. = μ) of finite thickness t. The emerging light is
View SolutionA ray of light is incident at the glass-water interface at an angle i. It merges finally parallel to the surface of water. Then, the value of μg would be
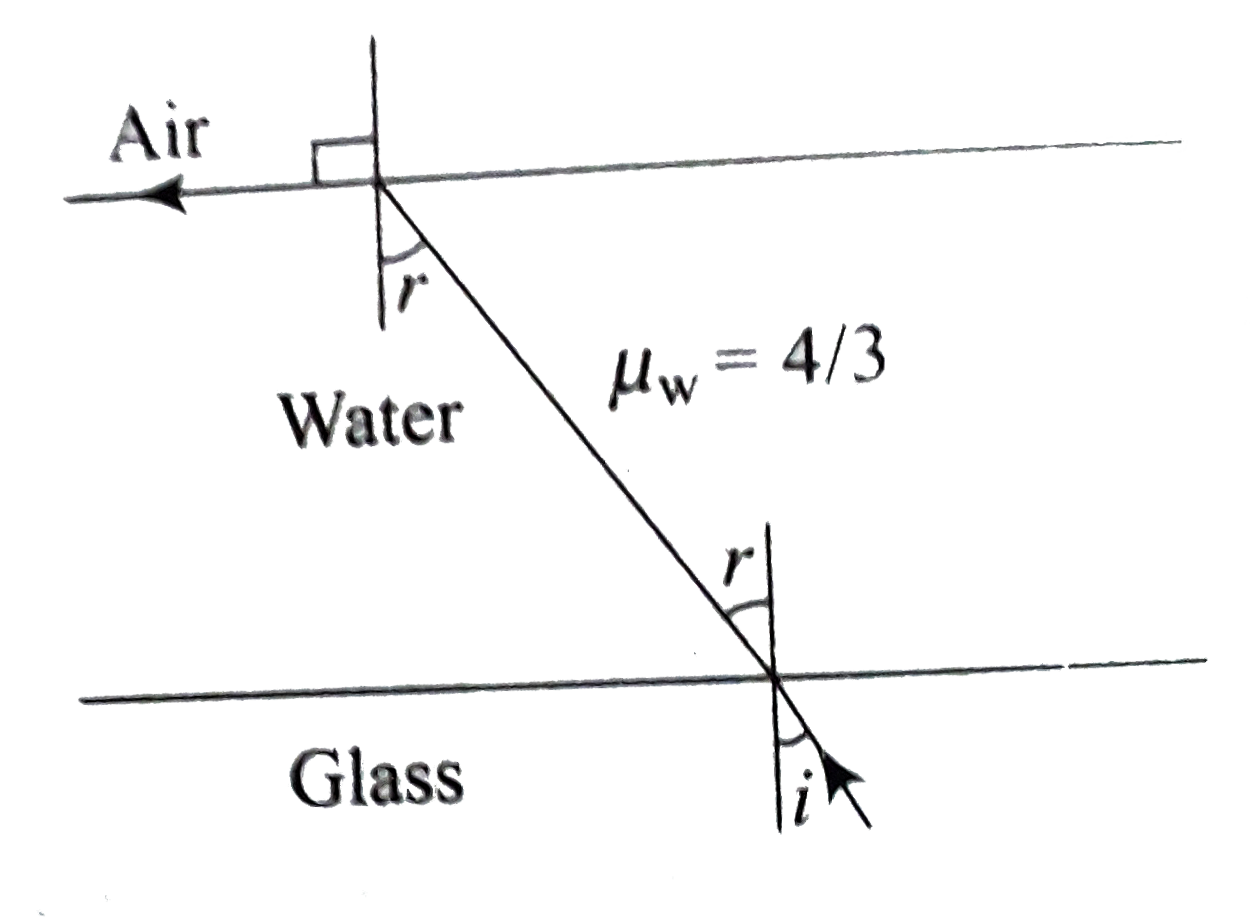 View Solution
View Solution

