A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting n→∞ , deduce the expression for the magnetic field at the centre of a circular current. Solution in Tamil
Step by step video & image solution for A regular polygon of n sides is formed by bending a wire of total length 2 pi r which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting n rarr oo , deduce the expression for the magnetic field at the centre of a circular current. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMAChapter:MAGNETIC FIELD DUE TO CURRENTExercise:Objective 2
Explore 7 Videos
- MAGNETIC FIELDBook:HC VERMAChapter:MAGNETIC FIELDExercise:Exercises
Explore 60 Videos
- MAGNETIC PROPERTIES OF MATTERBook:HC VERMAChapter:MAGNETIC PROPERTIES OF MATTERExercise:Exercise
Explore 9 Videos
Similar Questions
The magnetic field at the origin due to a current element I (→dl)placedataposi→n(→r)is
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionThe magnetic intensity H at the centre of a long solenoid carrying a current of 2.0A, is found to be 1500Am−1. Find the number of turns per centimetre of the solenoid.
View SolutionIn the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a. Net magnetic field at centre will be
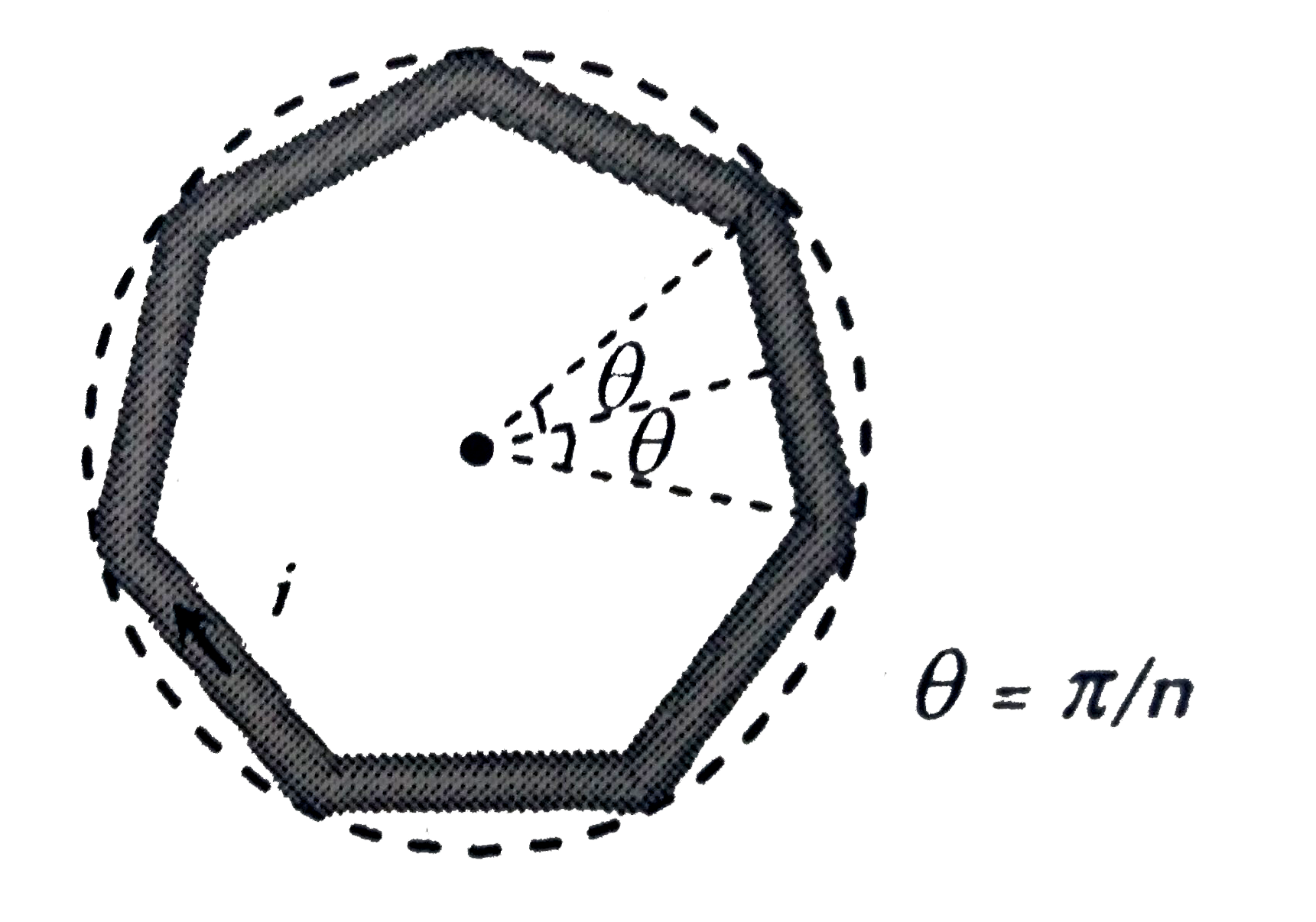
View SolutionA loop carrying current I has the shape of a regular polygon of n sides. If R is the distance from the centre to any vertex, then the magnitude of the magnetic induction vector →B at the centre of the loop is –
View SolutionThe magnetic field at the centre of a circular coil carrying current I ampere is B. It the coil is bent into smaller circular coil of n turns then its magnetic field at the centre is B, the ratio between B' and B is
View SolutionA regular polygon of n sides is formed by bending a wire of length L which carries if the magnetic field B at the centre of the polygon μ0in2sinπntanπnNπL, then find the value of N
View SolutionThe ratio of the magnetic field at the centre of a current carrying circular wire and the magnetic field at the centre of a semi-circular coil made from the same length of wire will be
View SolutionA current I flows in a thin wire in the shape of a regular polygon n sides. The magnetic induction at the centre of the polygon when n→∞ is (R is the radius of its circumcircle)
View SolutionIf a thin wire of length L is given the shape of a regular polygon of n sides and current I flows through it, what will be the net magnetic field at the centre of the polygon if n is infinity?
View SolutionA regular polygon of 'n sides is formed by bending a wire of length 2πR which carries a current i. Find the magnetic field at the centre of the polygon?
View SolutionMagnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
View SolutionState the expression for the magnetic field due to a circular are of wire carrying a current I. Hence find the magnetic field at the centre of circular coil and having n turns.
View SolutionIn the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a . Net magnetic field at centre will be
View SolutionThe magnetic field at the centre of a circular coil carrying current I ampere is B. It the coil is bent into smaller circular coil of n turns then its magnetic field at the centre is B, the ratio between B' and B is
View SolutionA long wire carrying a steady current is bent into a circular loop of one turn the magnetic field at the centre of the loop is B it is then bent into a circular coil of n turns the magnetic field at the centre of this coil of n turns will be
View Solution