A ring of mass m=1kg can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of L=0.7m from the rod as shown in figure.
![A ring of mass m=1kg can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of L=0.7m from the rod as shown in figure. At the other end of the string mass M=5kg is attached, lying over a smooth fixed inclined plane of inclination angle 37^@. The ring is held in level with the pulley and released. Determine the velocity of ring when the string makes an angle (alpha=37^@) with the horizontal. [sin 37^@=0.6]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V01_C08_E01_120_Q01.png)
At the other end of the string mass M=5kg is attached, lying over a smooth fixed inclined plane of inclination angle 37∘. The ring is held in level with the pulley and released. Determine the velocity of ring when the string makes an angle (α=37∘) with the horizontal. [sin37∘=0.6]
The correct Answer is:0ms−1
Let x is the vertical distance covered by the ring. Then
x=Ltan37∘=0.7×34
Δl=Lsec37∘−L
=L(sec37∘−1)
⇒L4=Δl

Δ= distance moved by block M
Now, from constraint relation
vM=vrcos37∘=45vr (i)
vr= velocity of ring,
vM= velocity of the block at this instant
From work energy theorem, we get
Wgravity=ΔKE
−mgx+MgΔlsin37∘+12mv2r+12Mv2M=0 (ii)
On solving Eqs. (i) and (ii), we get
vr=0ms−1
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A smooth ring A of mass 4 kg can slide on a fixed smooth horizontal rod. A string tied to the ring passes over a fixed pulley and carries a block B of mass 2 kg as shown in the figure. At the initial instant, the string attached to the ring makes an angle 60° with the horizontal rod. If the system is released from rest, the initial acceleration of the ring is?
View SolutionA smooth ring A of mass m can slide on a fixed horizontal rod. A string tied to the ring passes over a fixed pulley B and carries a block C of ma M(=2m) as shown in figure. At an instant the string between the ring and the pulley makes an angle θ with the rod. a. Show that, if the ring slides with a pspeed v, the blockdescends with speed vcosθ, b. With whast acceleration will the ring starts moving if the system is released from rest with θ=300
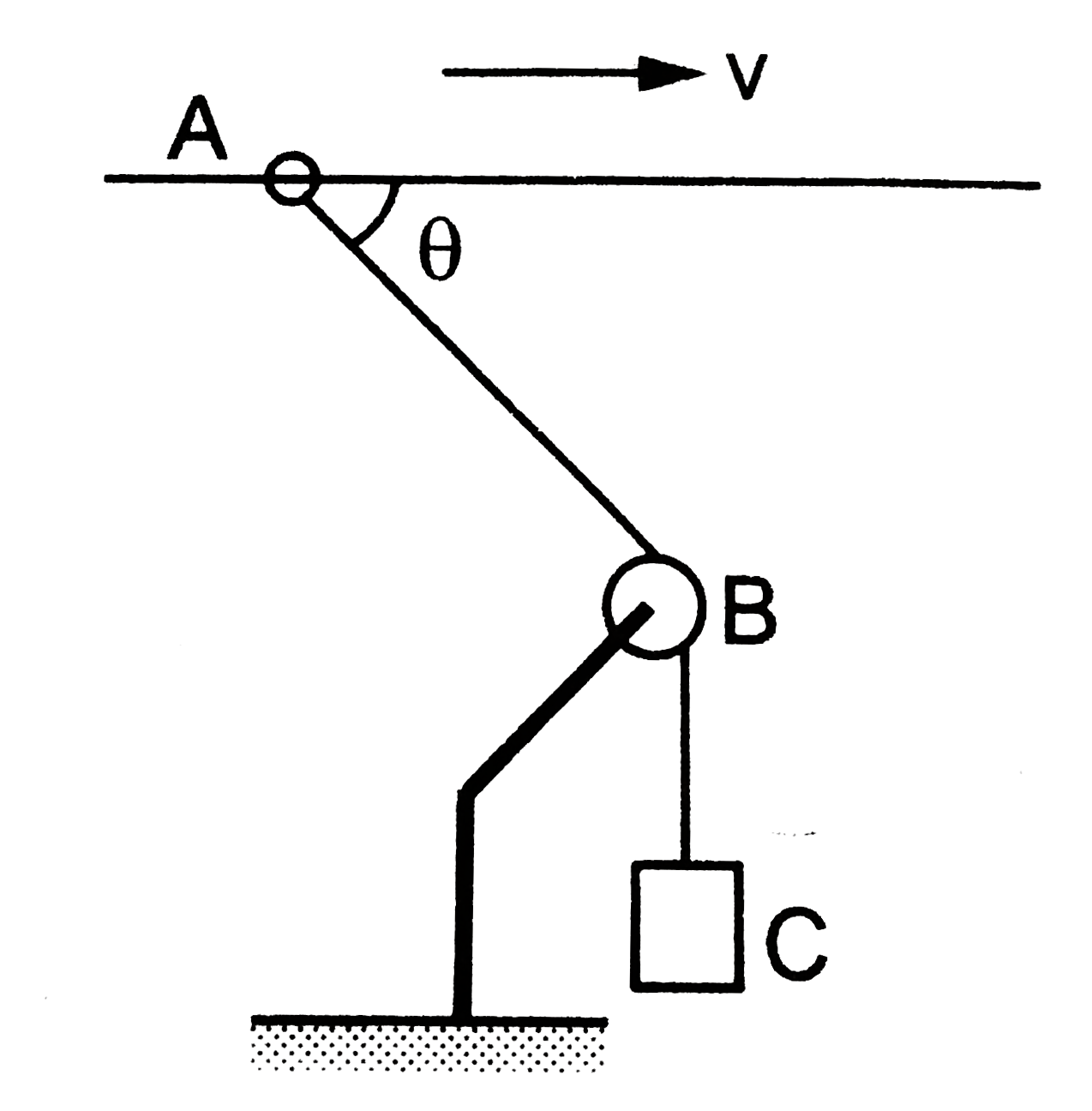
View Solution
Knowledge Check
A smooth ring of mass m can slide on a fixed horizontal rod. A string tied to the ring pases over a fixed pulley B and carries a block C of mass 2m as shown below. As the ring starts sliding
 AThe acceleration of the ring is 2gcosθ1+2cos2θBThe acceleration of the block is 2g1+2cos2θCThe tension in the string is 2mg1+2cos2θDIf the block descends with velocity v then the ring slides with velocity vcosθ
AThe acceleration of the ring is 2gcosθ1+2cos2θBThe acceleration of the block is 2g1+2cos2θCThe tension in the string is 2mg1+2cos2θDIf the block descends with velocity v then the ring slides with velocity vcosθTwo masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
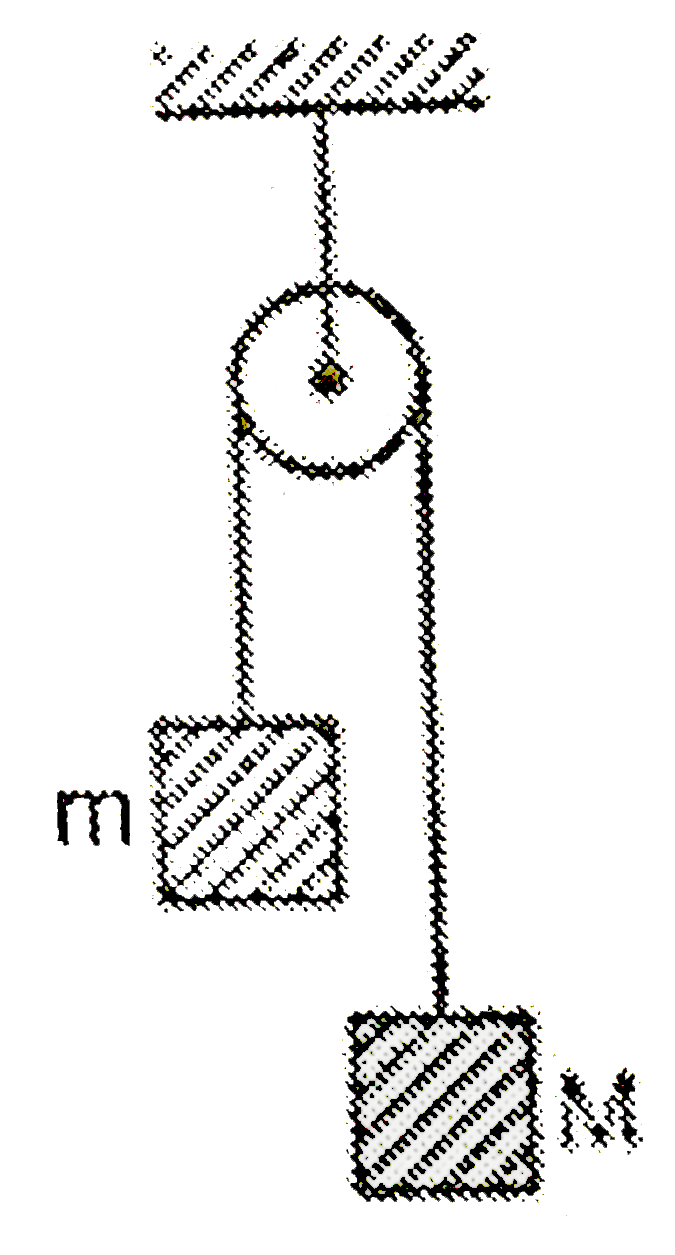 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)gTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
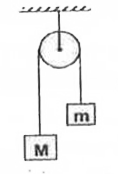 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
A ring of mass m can freely slide on a smooth vertical rod. The ring is symmetrically attached with two springs, as shown, each of stiffness k. Ring is displaced such that each spring makes an angle θ with the horizontal. If the ring is slightly displaced vertically, then time period is.......
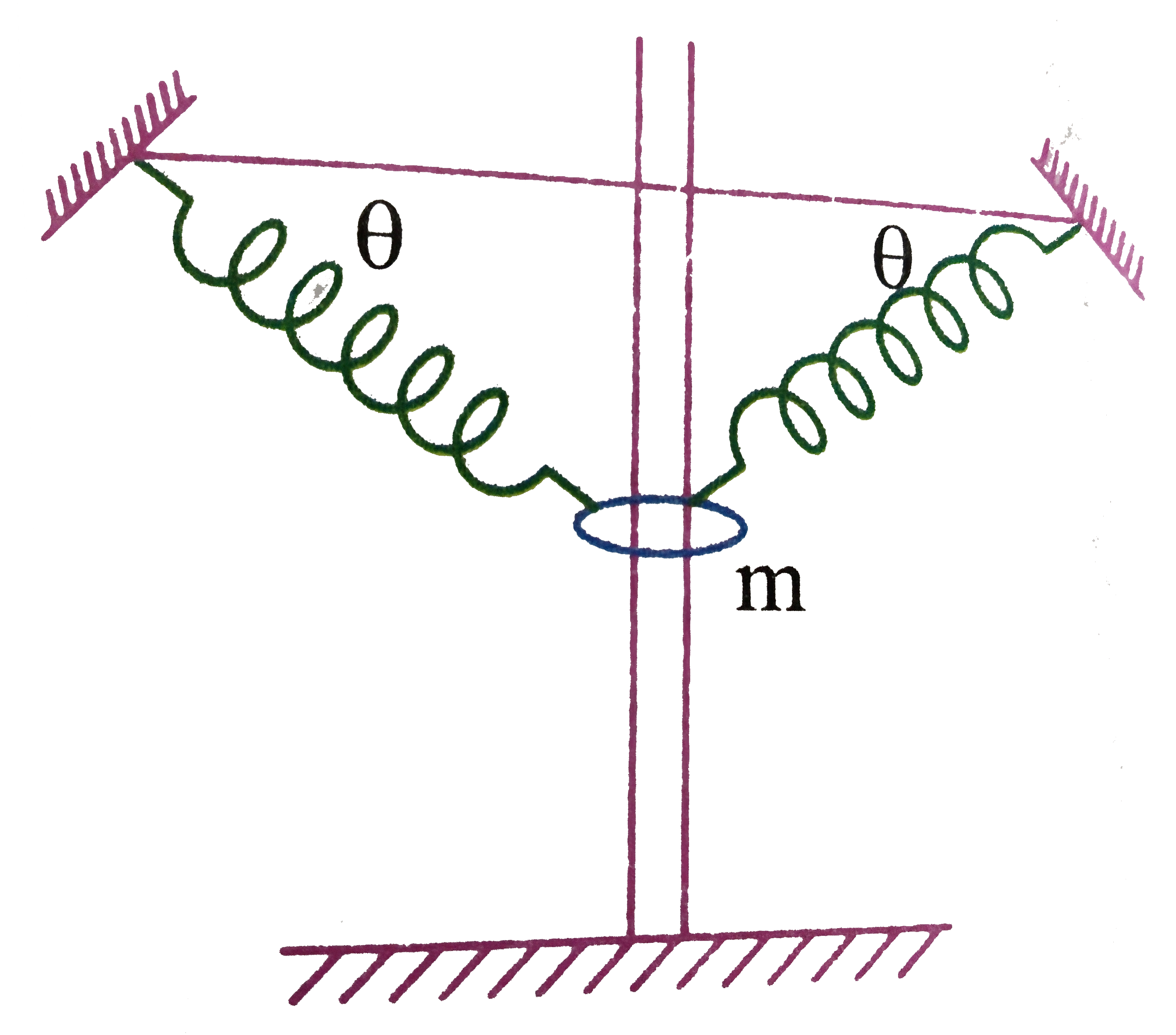
View SolutionTwo bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
View SolutionTwo masses ,each equal to m ,are arrached to one another by a massless string passing over a smooth pulley the tension in the string is :
View Solution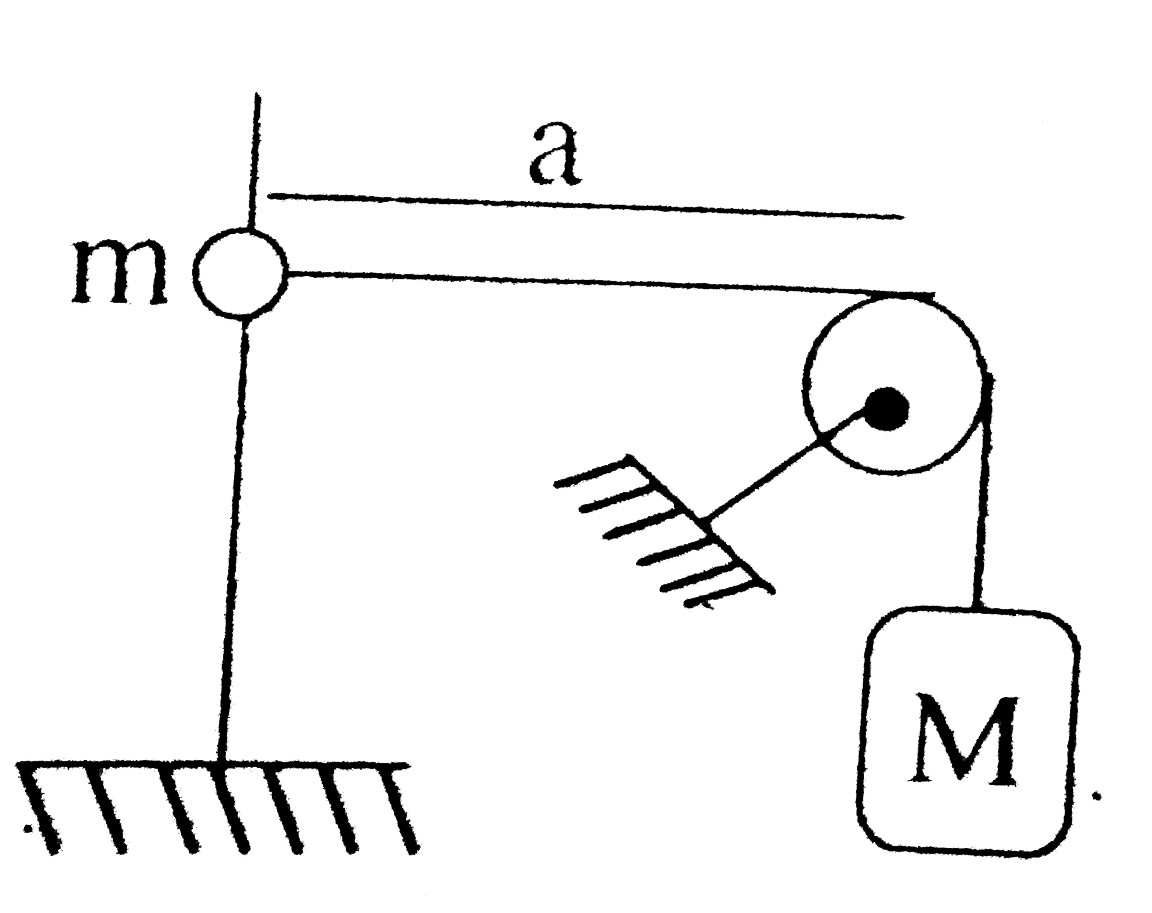
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string is
View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View Solution
