A ring of radius 0.1m is made out of thin metallic wire of area of cross section 10−6m2. The ring has a uniform charge of π coulombs. Find the change in the radius of the rig when a charge of 10−8C is placed at the center of the ring. Young's modulus of hte metal is 2×1011Nm−2.
The correct Answer is:2.25 mm
To solve the problem step by step, we will follow the outlined approach based on the information given in the question.
Step 1: Understand the problem
We have a ring of radius r=0.1m with a uniform charge Q=πC. A charge q=10−8C is placed at the center of the ring. We need to find the change in the radius of the ring when this charge is introduced, given the Young's modulus Y=2×1011N/m2.
Step 2: Calculate the charge per unit length (λ)
The total length L of the ring can be calculated using the formula for the circumference of a circle:
L=2πr=2π(0.1)=0.2πm
Now, we can find the charge per unit length λ:
λ=QL=π0.2π=10.2=5C/m
Step 3: Determine the force on a small arc of the ring
Consider a small arc of the ring subtending an angle θ at the center. The force F on this arc due to the charge q at the center can be calculated using Coulomb's law. The force on the arc can be expressed as:
F=k⋅q⋅λ⋅θ⋅rr2
where k is Coulomb's constant (k=9×109N m2/C2).
Step 4: Calculate the tension in the wire
The tension T in the wire can be related to the force acting on the small arc. The vertical components of the tension must balance the force due to the charge at the center:
F=2Tsin(θ2)≈Tθ(for small θ)
Thus, we have:
T=Fθ
Step 5: Substitute the values into the tension formula
Substituting the expression for F:
T=k⋅q⋅λ⋅rr2⋅θ
Now, substituting λ=5C/m, q=10−8C, and r=0.1m:
T=9×109⋅10−8⋅5⋅0.1(0.1)2⋅θ
This simplifies to:
T=4500θN
Step 6: Calculate the change in radius using Young's modulus
Using the definition of Young's modulus:
Y=StressStrain=T/AΔR/R
Where A=10−6m2 is the cross-sectional area of the wire. Rearranging gives:
ΔR=T⋅RY⋅A
Substituting T=4500N, R=0.1m, Y=2×1011N/m2, and A=10−6m2:
ΔR=4500⋅0.12×1011⋅10−6=4502×105=2.25×10−3m=2.25mm
Final Answer
The change in the radius of the ring is ΔR=2.25mm.
---
We have a ring of radius r=0.1m with a uniform charge Q=πC. A charge q=10−8C is placed at the center of the ring. We need to find the change in the radius of the ring when this charge is introduced, given the Young's modulus Y=2×1011N/m2.
The total length L of the ring can be calculated using the formula for the circumference of a circle:
L=2πr=2π(0.1)=0.2πm
Now, we can find the charge per unit length λ:
λ=QL=π0.2π=10.2=5C/m
Consider a small arc of the ring subtending an angle θ at the center. The force F on this arc due to the charge q at the center can be calculated using Coulomb's law. The force on the arc can be expressed as:
F=k⋅q⋅λ⋅θ⋅rr2
where k is Coulomb's constant (k=9×109N m2/C2).
The tension T in the wire can be related to the force acting on the small arc. The vertical components of the tension must balance the force due to the charge at the center:
F=2Tsin(θ2)≈Tθ(for small θ)
Thus, we have:
T=Fθ
Substituting the expression for F:
T=k⋅q⋅λ⋅rr2⋅θ
Now, substituting λ=5C/m, q=10−8C, and r=0.1m:
T=9×109⋅10−8⋅5⋅0.1(0.1)2⋅θ
This simplifies to:
T=4500θN
Using the definition of Young's modulus:
Y=StressStrain=T/AΔR/R
Where A=10−6m2 is the cross-sectional area of the wire. Rearranging gives:
ΔR=T⋅RY⋅A
Substituting T=4500N, R=0.1m, Y=2×1011N/m2, and A=10−6m2:
ΔR=4500⋅0.12×1011⋅10−6=4502×105=2.25×10−3m=2.25mm
The change in the radius of the ring is ΔR=2.25mm.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct47videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct8videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type15videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
Similar Questions
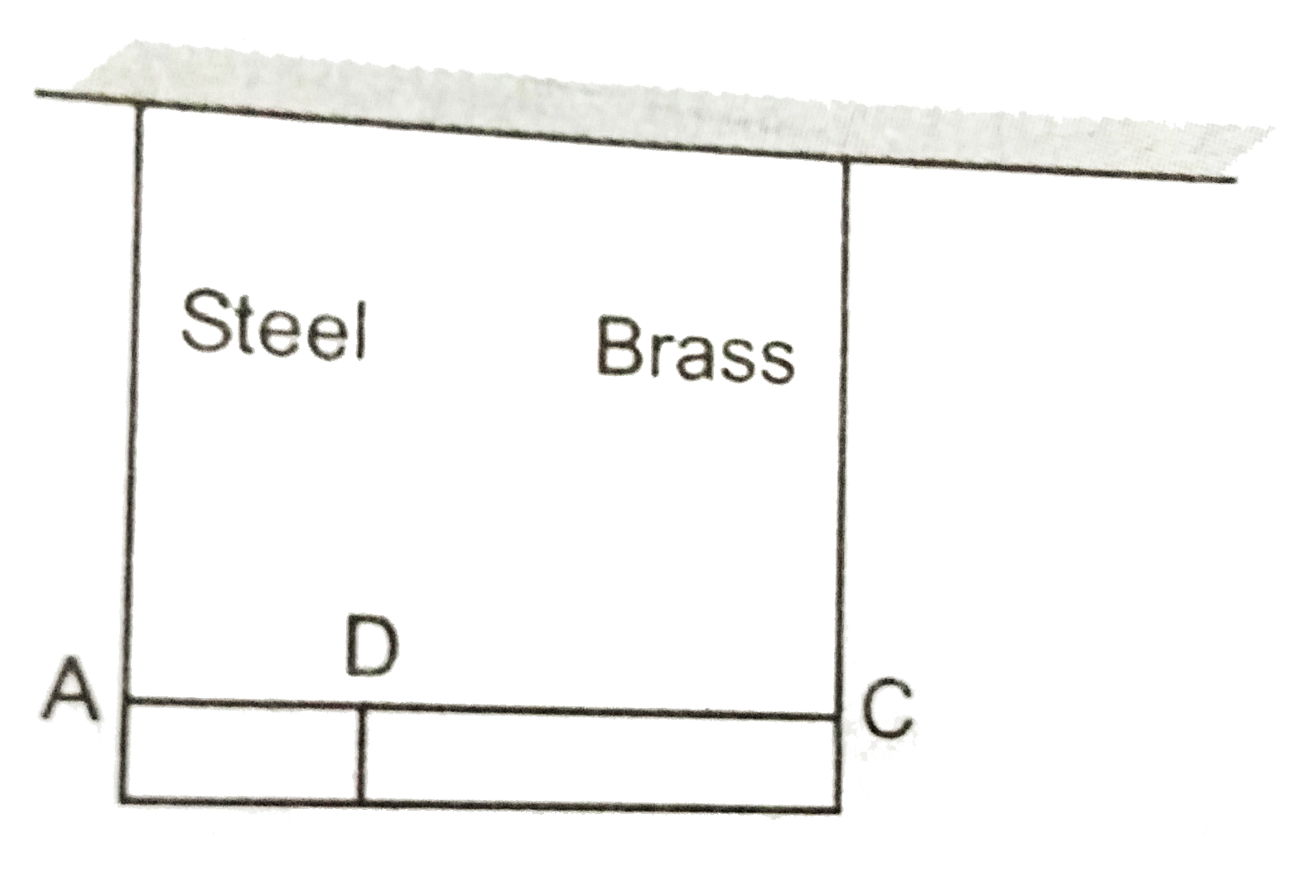
A light rod AC of length 2.00 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross-section 2×10−3m2. The position of point D from end A along the rod at which a weight may be hung to produce equal stress in both the wires is [Young's modulus of steel is 2×1011Nm2 and for brass is 1×1011Nm−2]
 View Solution
View SolutionA ring of charge with radius 0.5m has 0.002π m gap. If the ribg carries a charge of +1C the electric field at the center is
 View Solution
View SolutionFind the work done in stretching a wire Im long and area of cross section 0.03 cm under a load of 100 N if Young.s modulus of the material of the wire is 2×1011N/m2
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
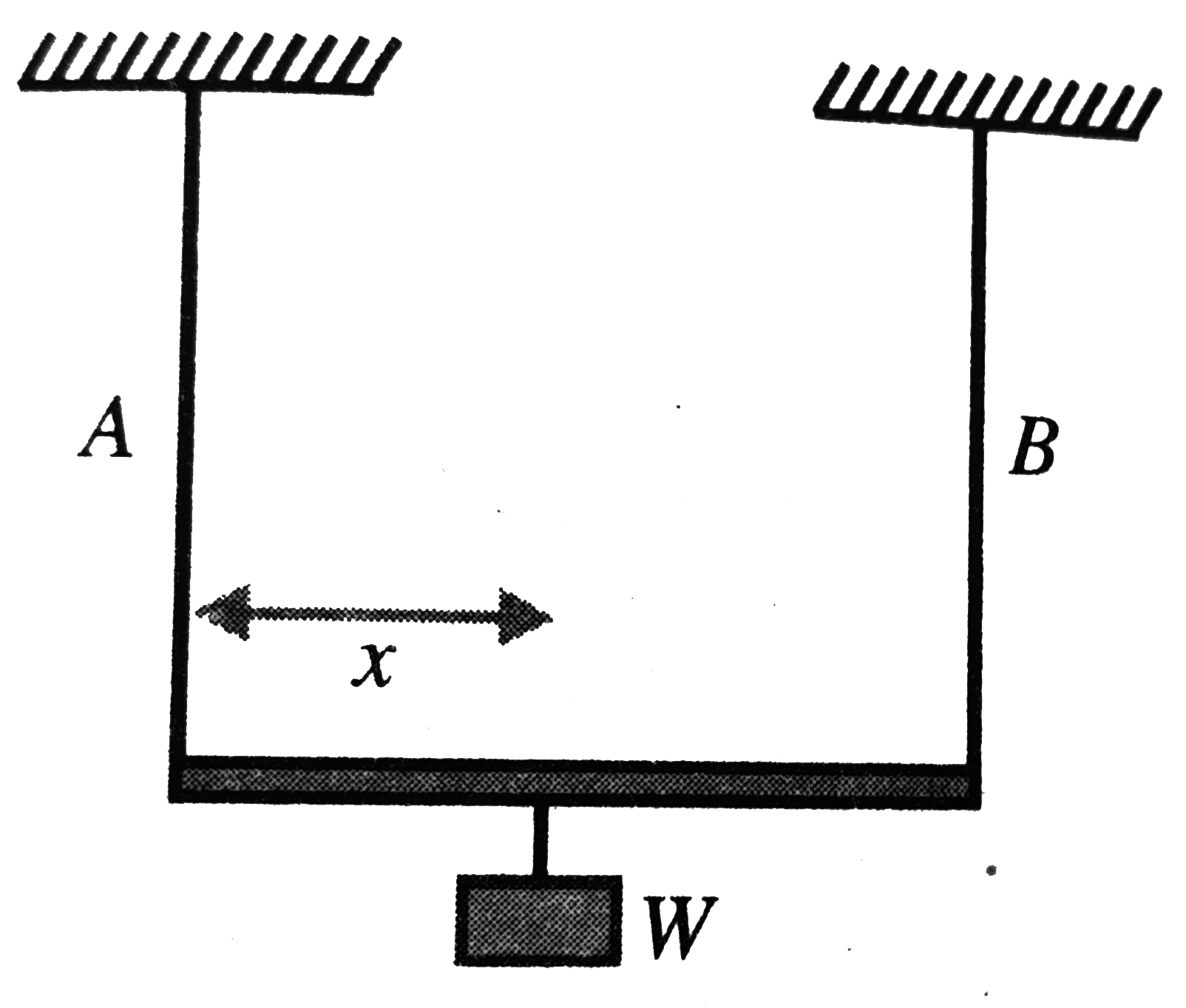
Determine the value of x so that equal stresses are produced in each wire.View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
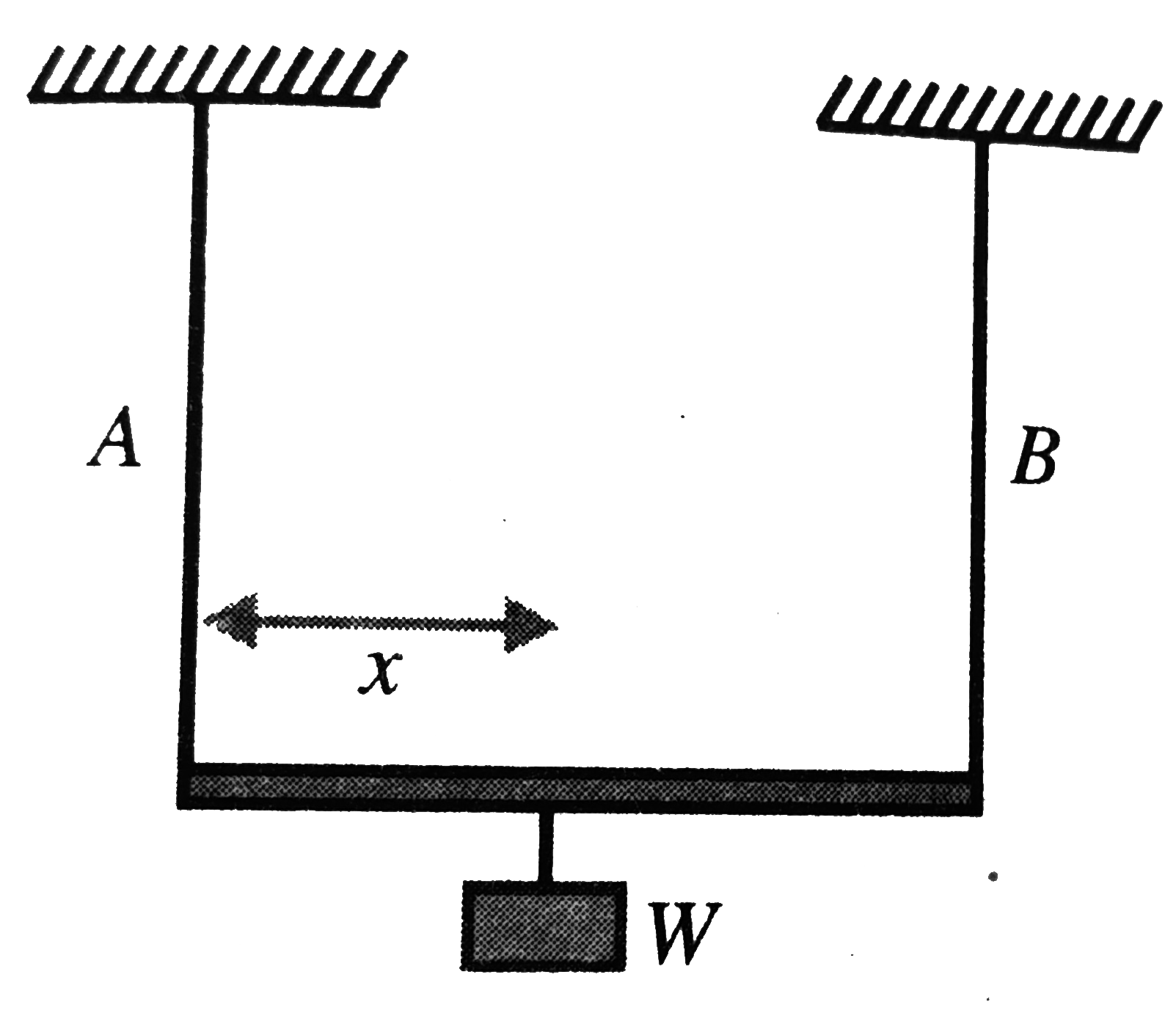
Determine the value of x so that equal strains are produced in each wireView SolutionA wire of length 1 m and area of cross section 2×10−6m2 is suspended from the top of a roof at one end and a load of 20 N is applied at the other end. If the length of the wire is increased by 0.5×10−4m, calculate its Young’s modulus (in 1011N/m2).
View SolutionA semicircular ring of radius 0.5 m is uniformly charged with a total charge of 1.5×10−9 coul. The electric potential at the centre of this ring is :
View SolutionFind the maximum energy per unit volume that can be stored in a metal wire when stretched, if its breaking stress is 1.3×108Nm−2 and Young's modulus of the material is 2.2×1011Nm−2 .
View SolutionA block of weight 10 N is fastened to one end of wire of cross-sectional area 4mm2 and is rotated ina vertical circle of radius 30 cm. The speed of the block at the bottom of the circle is 3ms−1. Find the elongation of the wire when the block is at the bottom of the circle . Young's modulus of the material of the wire =2×1011Nm−2.(g=10ms−2)
View SolutionA load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
View Solution
