A ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
ωoμkR2g
ωog2μkR
2ωoRμkg
ωoR2μkg
The correct Answer is:d
To solve the problem, we will analyze the motion of the ring as it transitions from pure rotational motion to rolling motion due to the effect of friction. Here are the steps to derive the time after which the ring starts rolling:
Step 1: Understand the Initial Conditions
The ring is initially rotating with an angular speed ω0 about a horizontal axis and is placed on a rough horizontal table. The coefficient of kinetic friction is μk.
Step 2: Identify Forces Acting on the Ring
When the ring is placed on the rough surface, the frictional force acts at the point of contact. This frictional force will provide a linear acceleration to the ring and will also create a torque that will decelerate its angular motion.
Step 3: Calculate Linear Acceleration
The frictional force F acting on the ring can be expressed as:
F=μkN
where N is the normal force, which equals the weight of the ring mg (where m is the mass of the ring). Thus, we have:
F=μkmg
Using Newton's second law, the linear acceleration a of the ring can be expressed as:
a=Fm=μkmgm=μkg
Step 4: Calculate Angular Deceleration
The torque τ due to friction is given by:
τ=F⋅R=μkmg⋅R
This torque causes an angular deceleration α given by:
τ=Iα
For a ring, the moment of inertia I is mR2. Thus, we have:
μkmg⋅R=mR2α
Cancelling m and R from both sides gives:
α=μkgR
Step 5: Relate Linear and Angular Motion
The relationship between linear velocity V and angular velocity ω is given by:
V=Rω
Initially, the linear velocity V is related to the angular velocity ω as:
V=Rω0
Step 6: Set Up Equations of Motion
For linear motion, we can use the equation:
V=U+at
Substituting U=Rω0 and a=μkg:
V=Rω0+μkgt
For rotational motion, we have:
ω=ω0−αt
Substituting α=μkgR:
ω=ω0−μkgRt
Step 7: Condition for Rolling Without Slipping
The condition for the ring to start rolling without slipping is when the linear velocity V equals the tangential velocity at the rim of the ring:
V=Rω
Substituting the expressions for V and ω:
Rω0+μkgt=R(ω0−μkgRt)
Step 8: Solve for Time t
Expanding and simplifying gives:
Rω0+μkgt=Rω0−μkgt
Bringing all terms involving t to one side:
μkgt+μkgt=0
2μkgt=0
Thus:
t=Rω02μkg
Final Answer
The time after which the ring starts rolling is:
t=Rω02μkg
The ring is initially rotating with an angular speed ω0 about a horizontal axis and is placed on a rough horizontal table. The coefficient of kinetic friction is μk.
When the ring is placed on the rough surface, the frictional force acts at the point of contact. This frictional force will provide a linear acceleration to the ring and will also create a torque that will decelerate its angular motion.
The frictional force F acting on the ring can be expressed as:
F=μkN
where N is the normal force, which equals the weight of the ring mg (where m is the mass of the ring). Thus, we have:
F=μkmg
Using Newton's second law, the linear acceleration a of the ring can be expressed as:
a=Fm=μkmgm=μkg
The torque τ due to friction is given by:
τ=F⋅R=μkmg⋅R
This torque causes an angular deceleration α given by:
τ=Iα
For a ring, the moment of inertia I is mR2. Thus, we have:
μkmg⋅R=mR2α
Cancelling m and R from both sides gives:
α=μkgR
The relationship between linear velocity V and angular velocity ω is given by:
V=Rω
Initially, the linear velocity V is related to the angular velocity ω as:
V=Rω0
For linear motion, we can use the equation:
V=U+at
Substituting U=Rω0 and a=μkg:
V=Rω0+μkgt
ω=ω0−αt
Substituting α=μkgR:
ω=ω0−μkgRt
The condition for the ring to start rolling without slipping is when the linear velocity V equals the tangential velocity at the rim of the ring:
V=Rω
Substituting the expressions for V and ω:
Rω0+μkgt=R(ω0−μkgRt)
Expanding and simplifying gives:
Rω0+μkgt=Rω0−μkgt
Bringing all terms involving t to one side:
μkgt+μkgt=0
2μkgt=0
Thus:
t=Rω02μkg
The time after which the ring starts rolling is:
t=Rω02μkg
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:HOTS HIGHER ORDER THINKING SKILL
Explore 8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:NCER EXAMPLAR PROBLEMS
Explore 8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:ANGULAR MOMENTUM IN CASE OF ROTATIONS ABOUT A FIXED AXIS
Explore 16 Videos
- PRACTICE PAPERSBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPERSExercise:All Questions
Explore 150 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
A disc of radius R is rotating with an angular ω0 about a horizontal axis it is placed on a horizontal table . The coefficient of kinetic friction is μk
(a) what was the velocity of its centre of mass before being brought in contact with a the table ?
(B) what happens to the linear velocity of a point on its rim when placed in contact with the table ?
(c ) what happes to the linear speed of the centre of mass when disc is placed in contact with the table ?
(d) which force is responsible for the effects in (b) and (C ) ?
(e) wht condition should be sattisfied for rolling to begin ?
(f) Calculate the time taken for the rolling to begin .
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View Solution
A disc of radius R is spun to an angualr speed ω0 about its axis and then imparted a horizontal velocity of magnitude ω0R4. The coefficient of friction is μ. The sense of rotation and direction of linear velocity are shown in the figure. The disc will return to its initial position.
View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA solid sphere of radius 2.45m is rotating with an angular speed of 10rad/s. When this rotating sphere is placed on a rough horizontal surface then after sometime it starts pure rolling. Find the linear speed of the sphere after it starts pure rolling.
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
View SolutionA hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
View SolutionA disc of the radius R is spun to an angular speed ω0 about its axis and then imparted a horizontal velocity of magnitude (at t = 0) with its plane remaining vertical. The coefficient of friction between the disc and the plane is μ . The sense of rotation and direction of its linear speed are shown in the figure . Choose the correct statement.
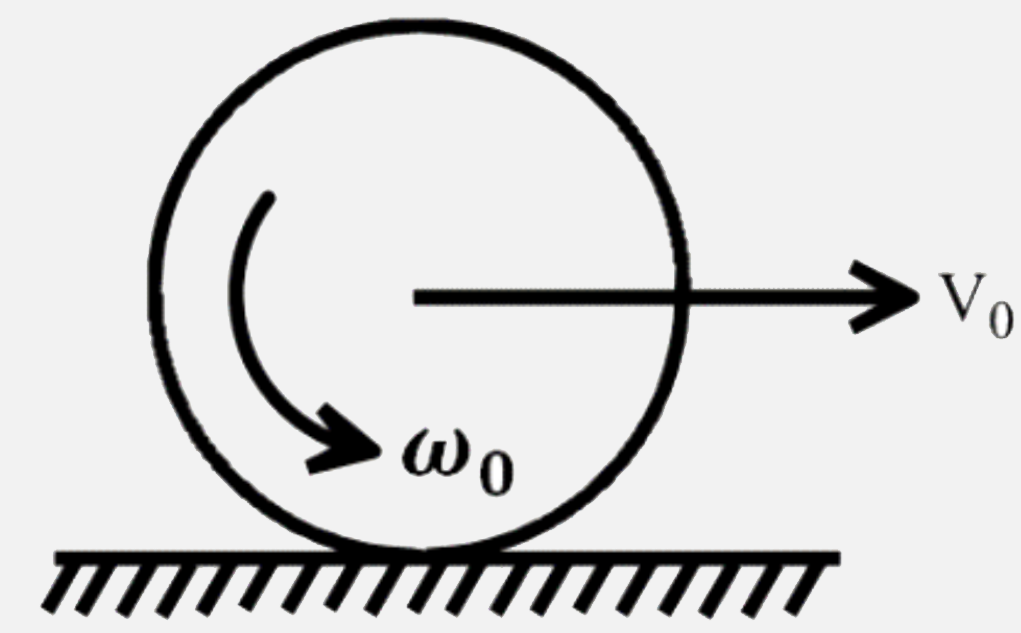
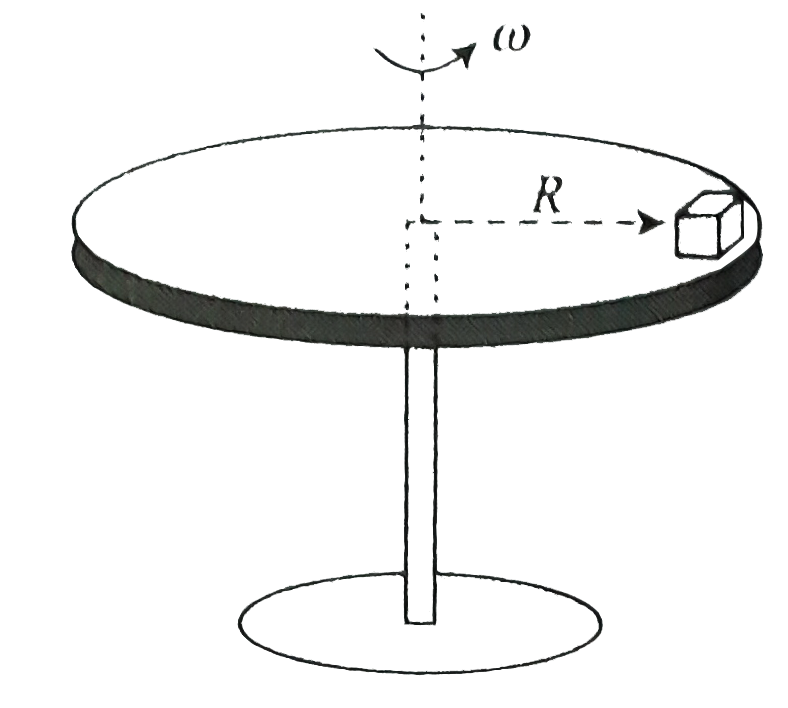
View SolutionA block of mass m is kept on the edge of a horizontal turn table of radius R which is rotating with constant angular verticle ω (along with the block ) about its axis . If coefficient of friction is μ, find the friction force between block and table.
View SolutionA uniform disc of mass m and radius R is rotated about an axis passing through its center and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficient of friction between the disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.
View Solution