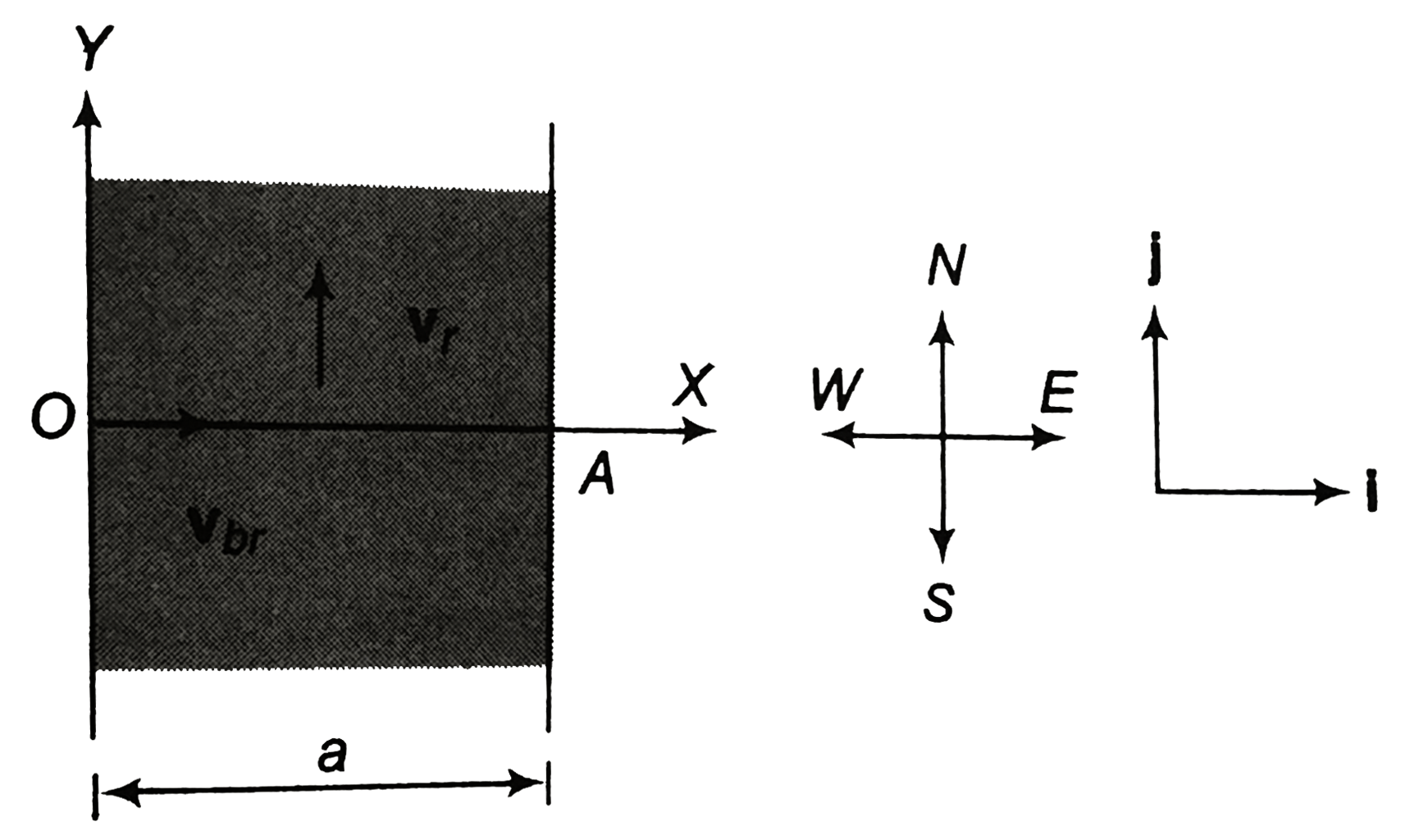
A river of width a with straight parallel banks flows due north with speed u. The points O and A are on opposite banks and A is due east of O. Coordinate axes $O_{x}$ and $O_{y}$ are taken in the east and north directions respectively. A boat, whose speed is v relative to water, starts from O and crosses the river. If the boat is steered due east and u varies with $x a s : u = x (a - x) \frac{v}{a^{2}} .$ Find
(a) equation of trajectory of the boat,
(b) time taken to cross the river,
(c) absolute velocity of boatman when he reaches the opposite bank,
(d) the displacement of boatman when he reaches the opposite bank from the initial position.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

(a) Let $v_{b r}$ be the velocity of boatman relative to
river, $v_{r}$ the velocity of river and $v_{b}$ is the absolute
velocity of boatman. Then,

$v_{b} = v_{b r} + v_{r}$
Given, $| v_{b r} | = v$ and $| v_{r} | = u$
Now $u = v_{y} = \frac{d y}{d t} = x (a - x) \frac{v}{a^{2}} ... (i)$
and $v = v_{x} = \frac{d x}{d t} ... . (i i)$
Dividing Eq. (i) by (i), we get
$\frac{d y}{d x} = \frac{x (a - x)}{a^{2}} or d y = \frac{x (a - x)}{a^{2}} d x$
$\int_{0}^{y} d y = \int_{0}^{x} \frac{x (a - x)}{a^{2}} d x$
or $y = \frac{x^{2}}{2 a} - \frac{x^{3}}{3 a^{2}} ... . . (i i i)$
This is the desired equation of trajectory.
(b) Time taken to cross the river is
$t = \frac{a}{v_{x}} = \frac{a}{v}$
(c) When the boatman reaches the opposite side,
$x = a or v_{y} = 0$ [From Eq.(i)]
Hence, resultant velocity of boatman is v along
positive x-axis or due east.
(d) From Eq. (iii)
$y = \frac{a^{2}}{2 a} - \frac{a^{3}}{3 a^{2}} = \frac{a}{6}$
At $x = a$ (at opposite bank)
Hence, displacement of boatman will be
$s = x ˆ i + y ˆ j or s = a ˆ i + \frac{a}{6} ˆ j$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

DC PANDEY ENGLISH-KINEMATICS-Subjective Questions

Home
Ask Doubt
Profile