A rocket is launched vertical from the surface of the earth of radius R with an initial speed v. If atmospheric resistance is neglected, then maximum height attained by the rocket is
h=R(2gRv2−1)
h=R(2gRv2+1)
h=R2(2gRv2−1)
h=R2(2gRv2+1)
The correct Answer is:A
To find the maximum height attained by a rocket launched vertically from the surface of the Earth with an initial speed v, we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Understand the Energy Conservation Principle
The total mechanical energy (kinetic + potential) at the surface of the Earth will be equal to the total mechanical energy at the maximum height.
Step 2: Write the Energy Equations
1. At the surface (point 1):
- Kinetic Energy (KE) = 12mv2
- Potential Energy (PE) = −GMmR
Total Energy at point 1:
E1=KE+PE=12mv2−GMmR
2. At the maximum height (point 2):
- Kinetic Energy (KE) = 0 (at maximum height, the velocity is zero)
- Potential Energy (PE) = −GMmR+h
Total Energy at point 2:
E2=0−GMmR+h
Step 3: Set the Total Energies Equal
Using the conservation of energy:
E1=E2
12mv2−GMmR=−GMmR+h
Step 4: Simplify the Equation
1. Cancel m from both sides (assuming m≠0):
12v2−GMR=−GMR+h
2. Rearranging gives:
12v2=GMR−GMR+h
Step 5: Combine the Right Side
1. Find a common denominator:
12v2=GM((R+h)−RR(R+h))
12v2=GMhR(R+h)
Step 6: Solve for h
1. Cross-multiply to isolate h:
12v2R(R+h)=GMh
12v2R2+12v2Rh=GMh
2. Rearranging gives:
12v2R2=GMh−12v2Rh
12v2R2=h(GM−12v2R)
3. Finally, solve for h:
h=12v2R2GM−12v2R
Step 7: Substitute GM with gR2
Using the relation g=GMR2:
h=12v2R2gR−12v2
Final Expression for Maximum Height
Thus, the maximum height h attained by the rocket is:
h=v2R2g−v2R
The total mechanical energy (kinetic + potential) at the surface of the Earth will be equal to the total mechanical energy at the maximum height.
1. At the surface (point 1):
- Kinetic Energy (KE) = 12mv2
- Potential Energy (PE) = −GMmR
E1=KE+PE=12mv2−GMmR
- Kinetic Energy (KE) = 0 (at maximum height, the velocity is zero)
- Potential Energy (PE) = −GMmR+h
E2=0−GMmR+h
Using the conservation of energy:
E1=E2
12mv2−GMmR=−GMmR+h
1. Cancel m from both sides (assuming m≠0):
12v2−GMR=−GMR+h
12v2=GMR−GMR+h
1. Find a common denominator:
12v2=GM((R+h)−RR(R+h))
12v2=GMhR(R+h)
1. Cross-multiply to isolate h:
12v2R(R+h)=GMh
12v2R2+12v2Rh=GMh
12v2R2=GMh−12v2Rh
12v2R2=h(GM−12v2R)
h=12v2R2GM−12v2R
Using the relation g=GMR2:
h=12v2R2gR−12v2
Thus, the maximum height h attained by the rocket is:
h=v2R2g−v2R
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (B) Chapter Exercises
31 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.6
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
A particle is projected vertically upward the surface of the earth (radius Re ) with a speed equal to one-fourth of escape velocity. The maximum height attained by it from the surface of the earth is Rek. Find k.
View SolutionA particle is projected vertically upwards the surface of the earth (radius Re) with a speed equal to one fourth of escape velocity what is the maximum height attained by it from the surface of the earth?
View Solution
Knowledge Check
A rocket is launched vertically from the surface of earth with an initial velocity v. How far above the surface of earth it will go? Neglect the air resistance.
AR(2gRv2−1)−1/2BR(2gRv2−1)CR(2gRv2−1)−1DR(2gRv2−1)2A rocket is launched vertically from the surface of the earth with an initial velocity v. How far above the surface of earth will it go? Neglect the air resistance. (where R is the radius of the earth )
AR(2gRv2−1)−1/2BR(2gRv2−1)CR(2gRv2−1)−1DR(2gRv2−1)2A particle is prjected vertically upwards the surface of the earth (radius Re) with a speed equal to one fourth of escape velocity what is the maximum height attained by it from the surface of the earth?
A1615ReBRe15C415ReDNone of these
A rocket of mass M is launched vertically from the surface of the earth with an initial speed V=√gR2 . Assuming the radius of the earth to be R and negligible air resistance, the maximum height attained by the rocket above the surface of the earth is RX where X is:
View SolutionA body is projected vertically upward from. the surface of the earth.with a velocity equal to half its escape velocity. If R is radius of the earth, then the maximum height attained by the,body is (Rn). Find n.
View SolutionA roket of mass M is launched vertically upwards from trhe surface of the earth with an intial speed v . Assuming the radius of the earth to be R and negligible air resistance, the maximum height attained by the roket above the surface of the earth is
View SolutionA body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to hall the escape velocity for that planet. The maximum height attained by the body is
View SolutionThe graph shown the variation of velocity of a rocket with time. Then, the maximum height attained by the rocket is.
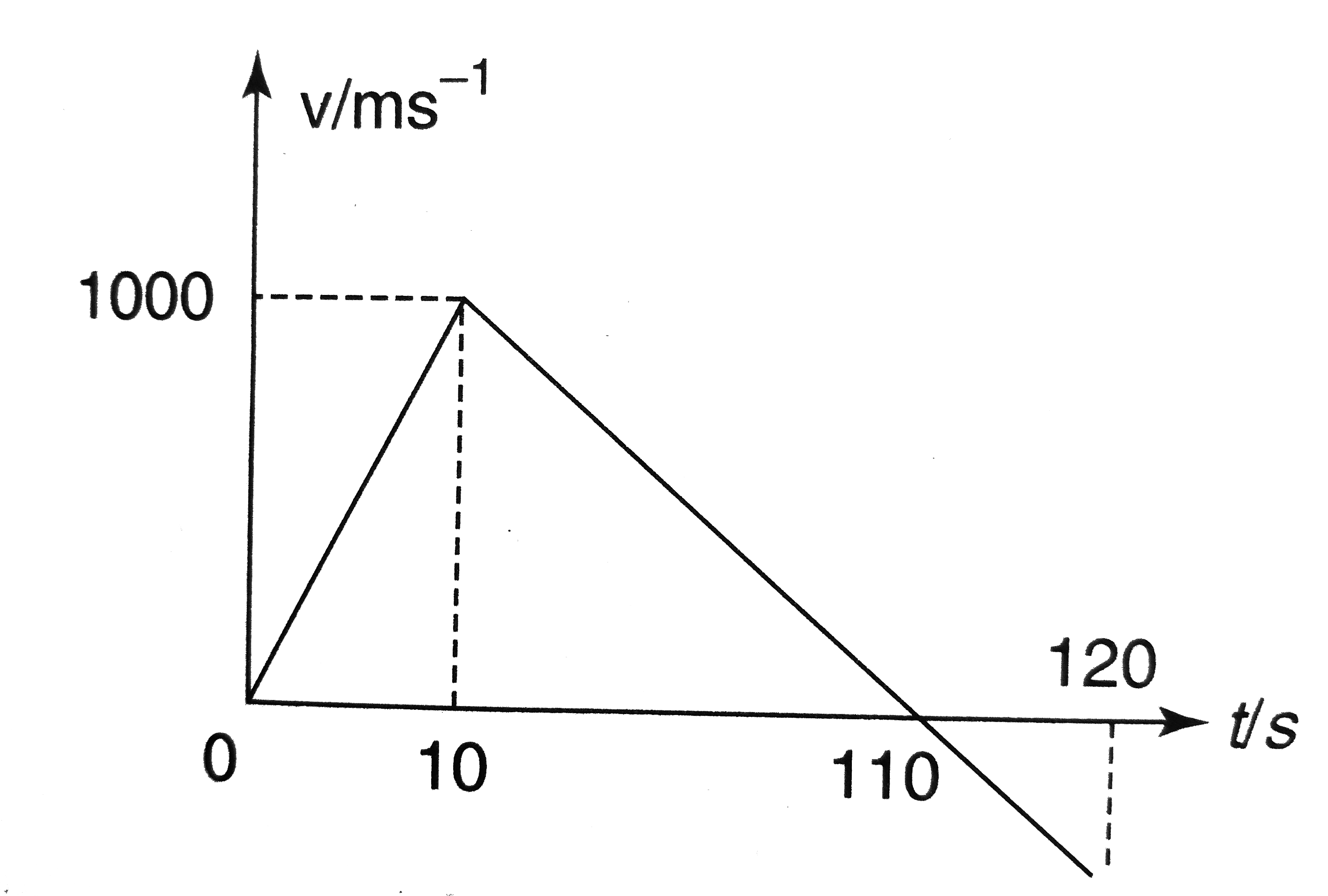
View Solution
