Energy of a satellite in circular orbit is E0. The energy required to move the satellite to a circular orbit of 3 times the radius of the initial orbit is
23E0
2E0
E03
32E0
The correct Answer is:A
Ei−E0=−GMm2rorEf=−GMm2(3r)=−GMm6r
∴W=Ef−Ej=−GMm3r=22E0.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (B) Chapter Exercises31videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.620videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE11videos
KINEMATICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The period of a satellite in a circular orbit of radius R is T, the period of another satellite in a circular orbit of radius 4R is
A4TBT/4C8TDT/8 - Question 2 - Select One
The period of a satellite in a circular orbit of radius R is T. The period of another satellite in circular orbit of radius 4 R is :
A4 TBT/4CT/8D8 T - Question 3 - Select One
Energy required to move a body of mass m from an orbit of radius 2R to 3R is
AGMm12R2BGMm3R2CGMm8RDGMm6R
The time period of a satellite in a circular orbit of radius R is T. The period of another satellite in a circular orbit of radius 9R is :
View SolutionMatch the Column I with Column II
For a satellite in circular orbit
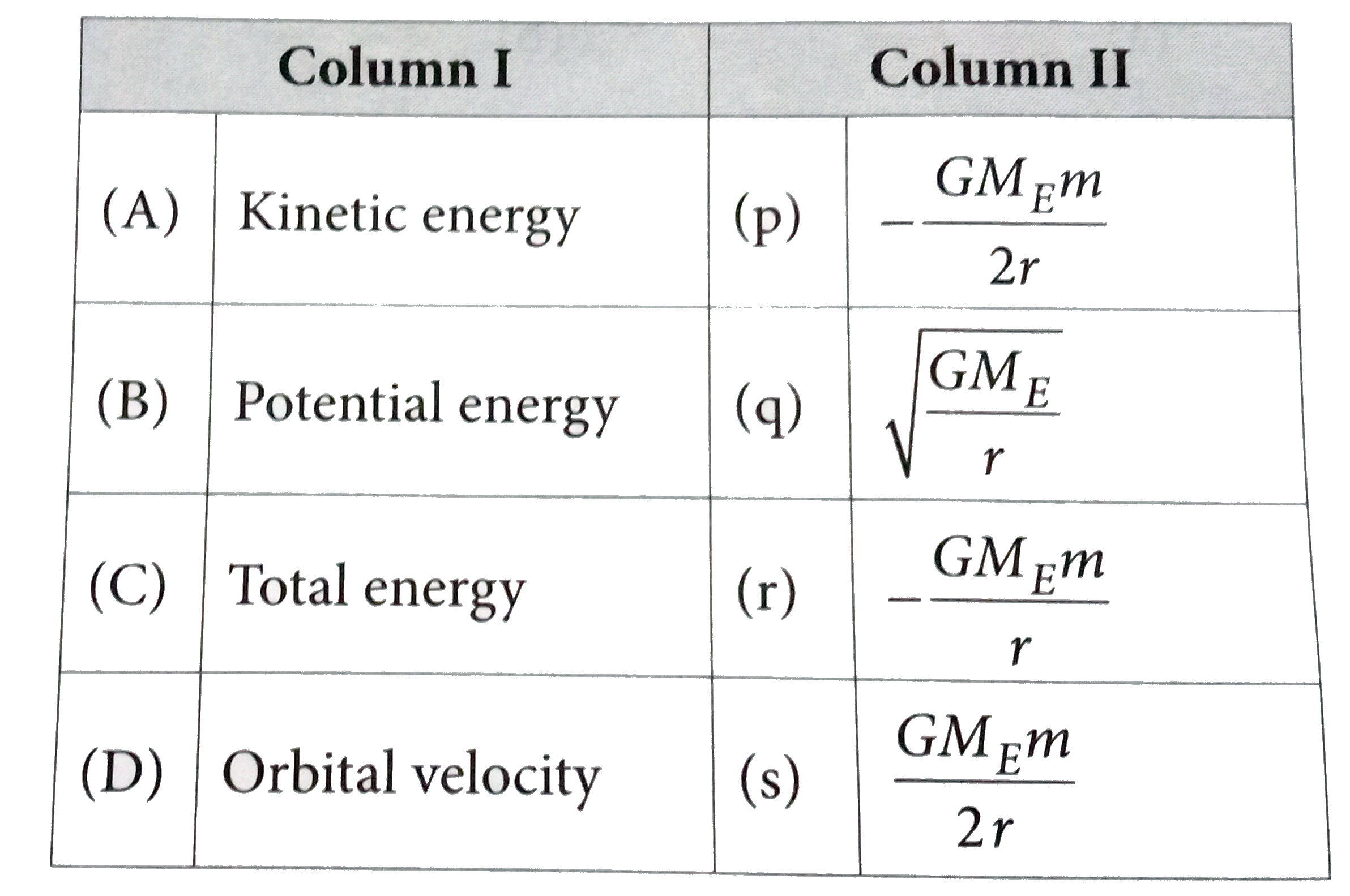
(where ME is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )View SolutionA 400 kg satellite is in a circular orbite of radius 2R around the earth how much energy is required to transfer it to circular orbit of radius 4R
View SolutionThe time period of a satellite in a circular orbit of radius R is T. The radius of the orbit in which time period is 8 T is
View SolutionA satellite of mass m is in a circular orbit of radius 2RE about the earth. The energy required to transfer it to a circular orbit of radius 4RE is (where ME and RE is the mass and radius of the earth respectively)
View Solution

