
A rod of length l forming an angle θ with the horizontal strikes a frictionless floor at A with its centre of mass velocity v0 and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.

Let v= lnear velocity of rod after impact (upwards)
ω= angular velocity of rod
and J= linear impulse at A during impact
then, J=△P=PfPi
J=mv−(−mv0)
∴J=m(v+v0) ..(i)
Angular impulse =△L
∴J(l2cosθ)=Iω=ml212ω ..(ii)

Collision is elastic (e=1)
∴ relative speed of approach = relative speed of separation at point of impact
v0=v+l2ωcosθ ..(iii)
Solving above equations we get
ω=6v0cosθl(1+3cosθ2θ)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A ping-pong ball strikes a wall with a velocity of 10ms−1. If the collision is perfectly elastic, find the velocity if ball after impact
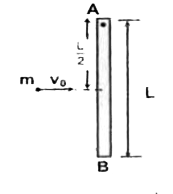
View SolutionA uniform rod AB which is free to swing in the vertical plane about a horizontal axis through A, is hanging freely. A particle of equal mass strikes the rod with a velocity v0 and gets stucks to it. Find the angular velocity of the combination immediately after the collision.
View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts

View SolutionTwo points of a rod move with velocity 3v and v perpendicular to the rod and in the same direction. Separated by a distance r. Then the angular velocity of the rod is :
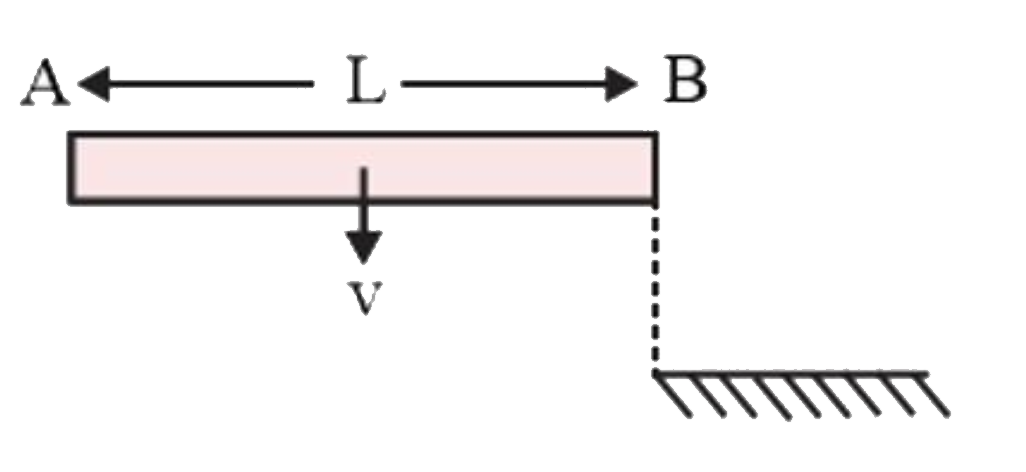
View SolutionA rod AB of length L and mass M is free to move on a frictionless horizontal surface. It is moving with a velocity v, as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact, the angular velocity of the rod AB, just after impact, is
View SolutionA uniform rod of mass M and length L, which is free to rotate about a fixed vertical axis through O, is lying on a frictionless horizontal table. A particle of equal mass strikes the rod with a velocity V0 and sticks to it. The angular velocity of the combination immediately after the collision is:
View SolutionA disk sliding with velocity u on a smooth horizontal plane strikes another identical disk kept at rest as shown in the figure. If the impact between the disks is perfectly elastic impact, find velocities of the disks after the impact.
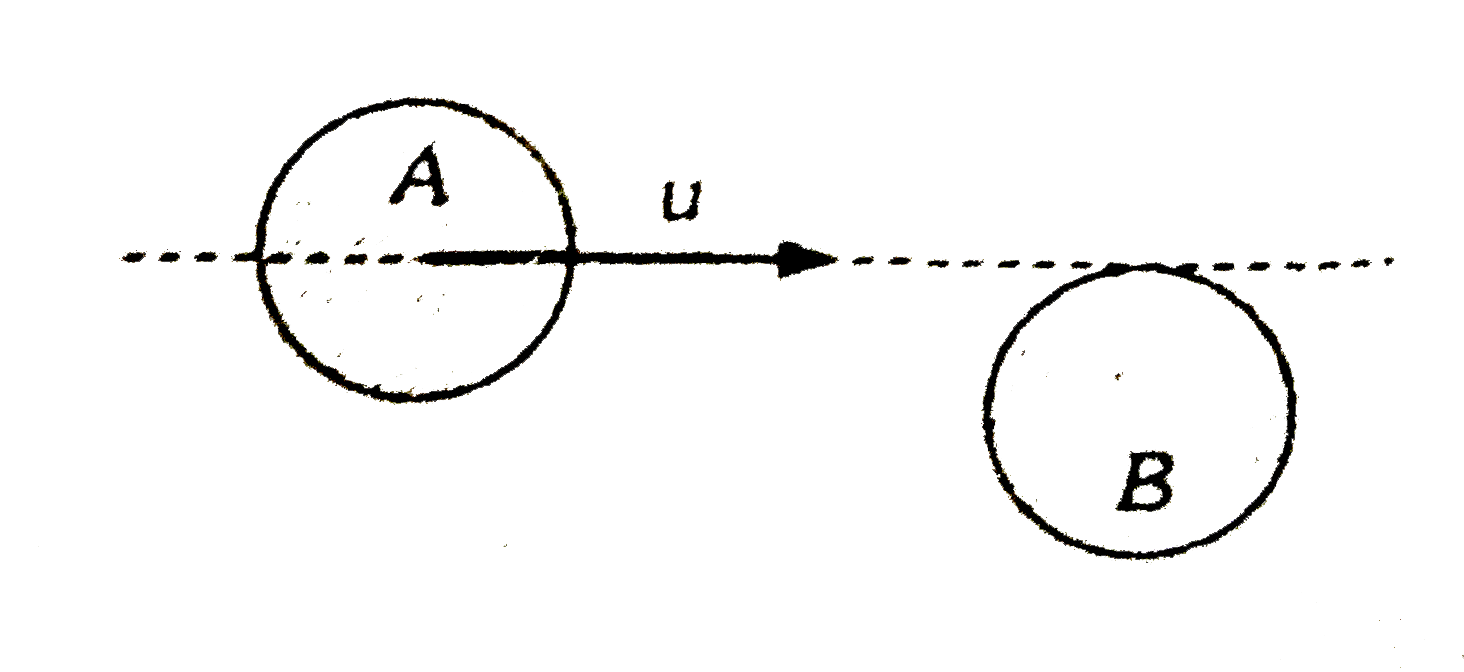
View SolutionA wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.

View SolutionA rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View SolutionA conducting rod AB of length l is projected on a frictionless frame PSRQ with velocity v0 at any instant. The velocity of the rod after time t is
View Solution
