A rod of length L has a total charge Q distributed uniformly along its length. It is bent in the shape of a semicircle. Find the magnitude of the electric field at the centre of curvature of the semicircle.
To find the magnitude of the electric field at the center of curvature of a semicircular rod with a total charge Q distributed uniformly along its length L, we can follow these steps:
Step 1: Determine the linear charge density
The linear charge density (λ) is defined as the total charge (Q) divided by the length (L) of the rod.
λ=QL
Step 2: Relate the length of the semicircle to its radius
When the rod is bent into the shape of a semicircle, the length of the semicircle is equal to half the circumference of a full circle. Therefore, we have:
L=πr
From this, we can express the radius (r) in terms of the length (L):
r=Lπ
Step 3: Use the formula for the electric field at the center of curvature
The electric field (E) at the center of curvature of a semicircular charge distribution can be calculated using the formula:
E=2kλrsin(α2)
For a semicircle, the angle (α) is π radians, so:
sin(α2)=sin(π2)=1
Substituting this into the electric field equation gives:
E=2kλr
Step 4: Substitute the values of λ and r into the electric field equation
Now substituting λ and r into the equation:
E=2k(QL)(Lπ)
Step 5: Simplify the expression
Now, simplify the expression:
E=2kQL⋅πL=2πkQL2
Final Answer
Thus, the magnitude of the electric field at the center of curvature of the semicircle is:
E=2πkQL2
The linear charge density (λ) is defined as the total charge (Q) divided by the length (L) of the rod.
When the rod is bent into the shape of a semicircle, the length of the semicircle is equal to half the circumference of a full circle. Therefore, we have:
The electric field (E) at the center of curvature of a semicircular charge distribution can be calculated using the formula:
Now substituting λ and r into the equation:
Now, simplify the expression:
Thus, the magnitude of the electric field at the center of curvature of the semicircle is:
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - worked out Examples
19 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
A circular wire loop of radius R carries a total charge q distributed uniformly over its length. A small length x(<<R) of the wire is cut off. Find the electric field at the centre due to the remaining wire.
View SolutionA 10 cm long rod carries a charge of +150μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both the ends of the rod.
View Solution
Knowledge Check
Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
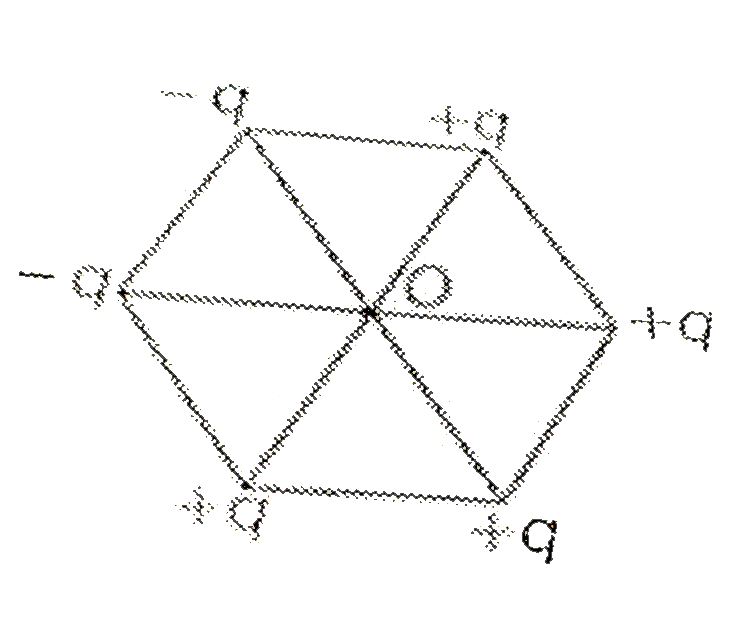
Find the magnitude of electric field at the centre of regular hexagon.A−qB−q6C+1.83qD−1.83q
A cjircular wire-loop of radius a carries a total charge Q distributed uniformly over its length . A small length dL of the wire is cut off. Find the electric field at the centre due to remaining wire.
View SolutionA wire of length l and charge q is bent in form of a semicircle. The charge is uniformly distributed over the length. The electric field at the centre of semicircle is
View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionA wire of length l and mass m is bent in the form of a semicircle. The gravitational field intensity at the centre of semicircle is

View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionA thin of length L is bent to form a semicircle. The mass of rod is M. What will be the gravitational potential at the centre of the circle ?
View SolutionA charge Q is uniformly distributed over a rod of length ι. Condider a hypothetical cube of edge ι with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
View Solution
