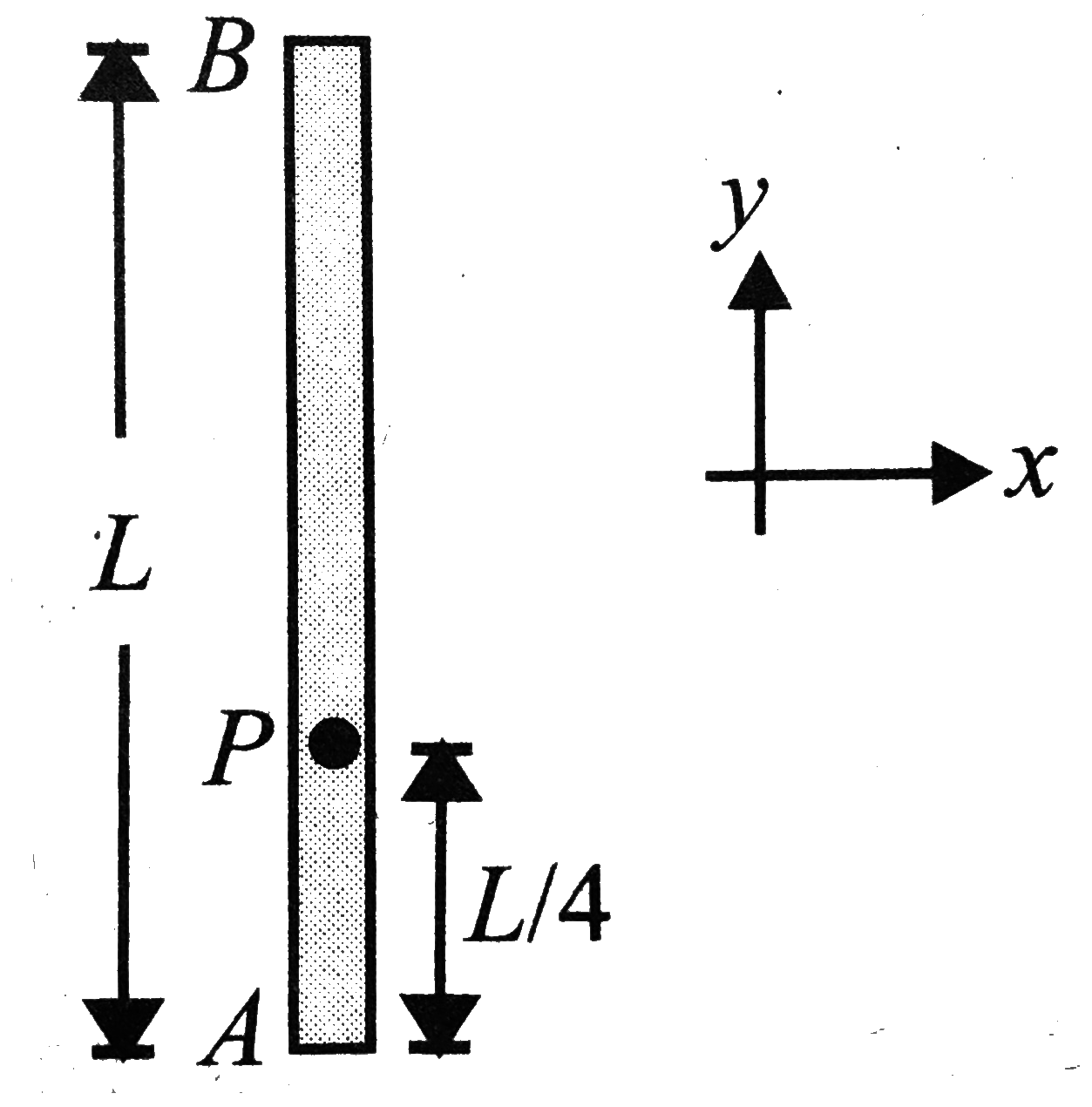
A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is.. And on B is......
NA=2w(1−x/d),NB=wx/d
NA=w(1−x/d),NB=wx/d
NA=2w(1−x/d),NB=2wx/d
NA=wx/d,NB=w(1−xd)
The correct Answer is:B
To solve the problem, we need to find the normal reactions at points A and B when a rod of weight W is supported by two parallel knife edges A and B, with the center of mass of the rod located at a distance x from A and the distance between A and B being d.
1. Identify the Forces:
- The rod has a weight W acting downwards at its center of mass.
- There are normal reactions NA at point A and NB at point B acting upwards.
2. Set Up the Moment Equation About Point B:
- To find the normal reaction at A (NA), we can take moments about point B.
- The moment due to the weight of the rod about point B is W×(d−x) (the distance from B to the center of mass).
- The moment due to the normal force at A is NA×d (the distance from A to B).
- Setting the sum of moments about point B to zero for equilibrium:
NA⋅d−W⋅(d−x)=0
3. Solve for NA:
- Rearranging the equation gives:
NA⋅d=W⋅(d−x)
- Dividing both sides by d:
NA=W⋅(d−x)d
- This can also be expressed as:
NA=W(1−xd)
4. Set Up the Moment Equation About Point A:
- Now, to find the normal reaction at B (NB), we take moments about point A.
- The moment due to the weight of the rod about point A is W⋅x (the distance from A to the center of mass).
- The moment due to the normal force at B is NB⋅d:
W⋅x−NB⋅d=0
5. Solve for NB:
- Rearranging the equation gives:
NB⋅d=W⋅x
- Dividing both sides by d:
NB=W⋅xd
Final Answers:
- The normal reaction at point A is:
NA=W⋅(d−x)d
- The normal reaction at point B is:
NB=W⋅xd
- The rod has a weight W acting downwards at its center of mass.
- There are normal reactions NA at point A and NB at point B acting upwards.
- To find the normal reaction at A (NA), we can take moments about point B.
- The moment due to the weight of the rod about point B is W×(d−x) (the distance from B to the center of mass).
- The moment due to the normal force at A is NA×d (the distance from A to B).
- Setting the sum of moments about point B to zero for equilibrium:
NA⋅d−W⋅(d−x)=0
- Rearranging the equation gives:
NA⋅d=W⋅(d−x)
- Dividing both sides by d:
NA=W⋅(d−x)d
- This can also be expressed as:
NA=W(1−xd)
- Now, to find the normal reaction at B (NB), we take moments about point A.
- The moment due to the weight of the rod about point A is W⋅x (the distance from A to the center of mass).
- The moment due to the normal force at B is NB⋅d:
W⋅x−NB⋅d=0
- Rearranging the equation gives:
NB⋅d=W⋅x
- Dividing both sides by d:
NB=W⋅xd
- The normal reaction at point A is:
NA=W⋅(d−x)d
- The normal reaction at point B is:
NB=W⋅xd
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct
86 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at a distance x from A.
View SolutionA uniform metre rod is bent into L shape with the bent arms at 90∘ to each other. The distance of the centre of mass from the bent point is
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
The acceleration of the centre of mass of the rod is
View SolutionA rod is of length 3 m and its mass acting per unit length is directly proportional to distance x from its one end. The centre of gravity of the rod from that end will be at
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance l6 from the centre towards A of the rod after time t=πml12J is.
View Solution
Shown in the figure is rigid and uniform one meter long rod AB held in horizontal position by two strings tied to its ends and attached to the ceiling . The rod is of mass 'm' and has another weight of mass 2 m hung at a distance of 75 cm from A . The tension in the string at A is :
View Solution
