A rope of length L and mass per unit length λ passes over a disc shaped pulley of mass M and radius R. The rope hangs on both sides of the pulley and the length of larger hanging part is l. The pulley can rotate about a horizontal axis passing through its centre. The system is released from rest and it begins to move. The pulley has no friction at its axle and the rope has large enough friction to prevent it from slipping on the pulley.
(a) Find the acceleration of the rope immediately after it is released.
(b) Find the horizontal component of the force applied by the axle on the pulley immediately after the system is released
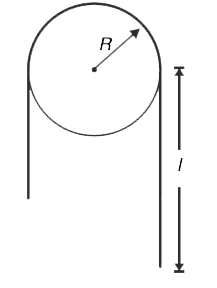
The correct Answer is:(a) λg(2l+πR−L)(λL+M2)
Topper's Solved these Questions
Similar Questions
Two masses 2m and m are attached to the ends of the card which passes over a pulley of mass m and radius R. Calculate the tension in the wire on both sides of the pulley. Assume no slipping.
View SolutionIf the system is released from rest, determine the speeds of both masses after B has moved 1 m. Neglect friction, the masses of pulleys and inextensible string.
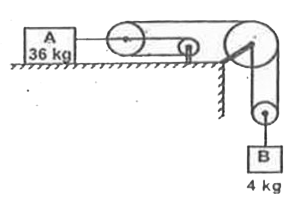
View Solution
Knowledge Check
- Question 1 - Select One
A string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
AmgB(M+m)gCMmg(M+2m)D2mg(M+2m) - Question 2 - Select One
The moment of inertia of a cylinder of radius R, length L and mass M about an axis passing through its centre of mass and normal to its length is
AML212BMR24CM[L212+R24]DM[L212+R22] - Question 3 - Select One
A uniform disc of mass m and radius r and a point mass m are arranged as shown in the figure. The acceleration of point mass is :( Assume there is no slipping between pulley and thread and the disc can rotate smoothly about a fixed horizontal axis passing through its centre and perpendicular to its plane )
Ag2Bg3C2g3Dnone of these
If the system is released from rest, determine the speeds of both masses after B has moved 1 m. Neglect friction, the masses of pulleys and inextensible string.
View SolutionA uniform disc of mass m and radius r and a point mass m are arranged as shown in the figure. The acceleration of point mass is :( Assume there is no slipping between pulley and thread and the disc can rotate smoothly about a fixed horizontal axis passing through its centre and perpendicular to its plane )
View Solution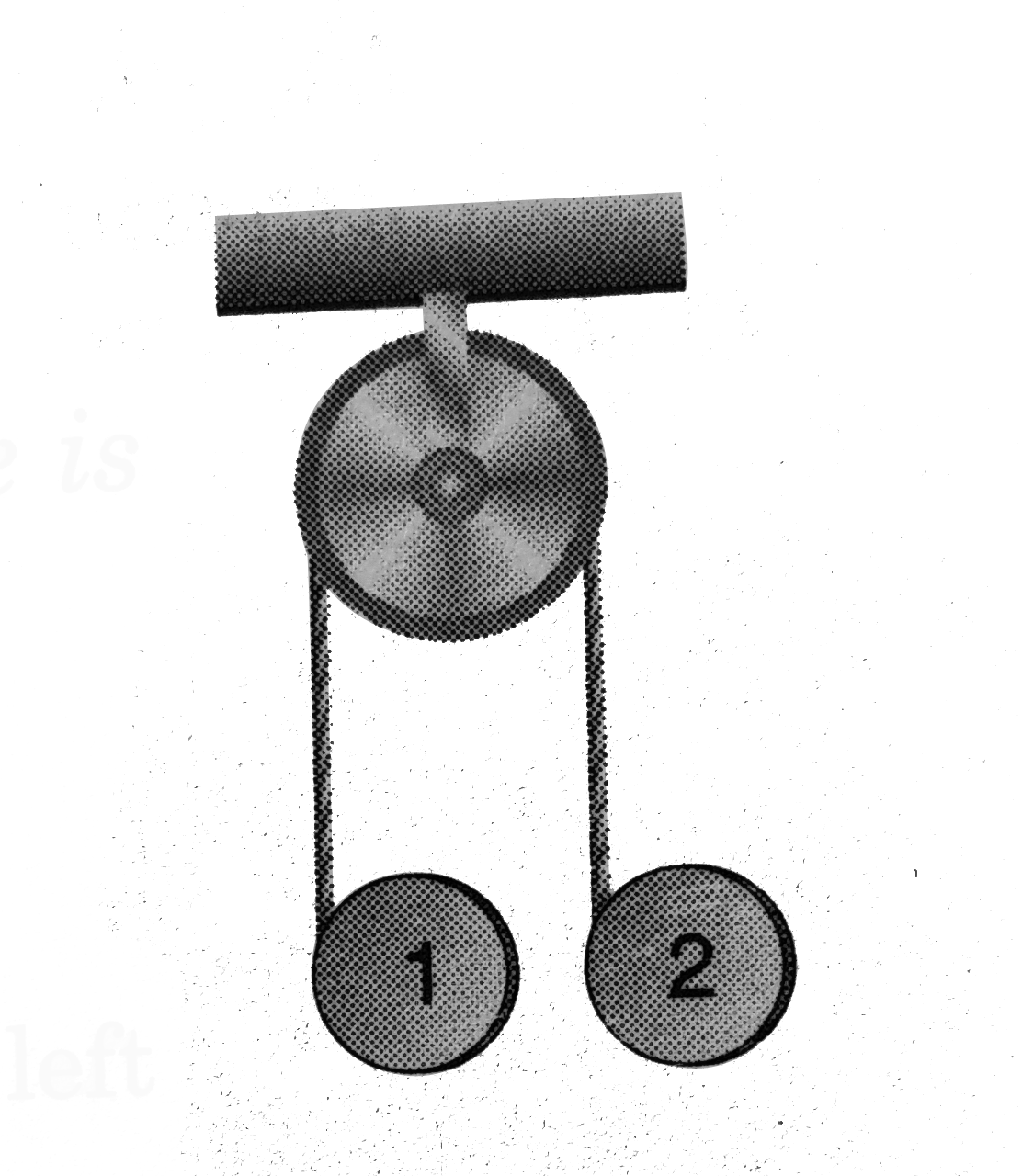
A thread is wound around two discs on either sides. The pulley and the two discs have the same mass and radius. There is no slipping at the pulley and no friction at the hinge. Find out the acceleration of the two discs and the angular acceleration of the pulley.View Solution-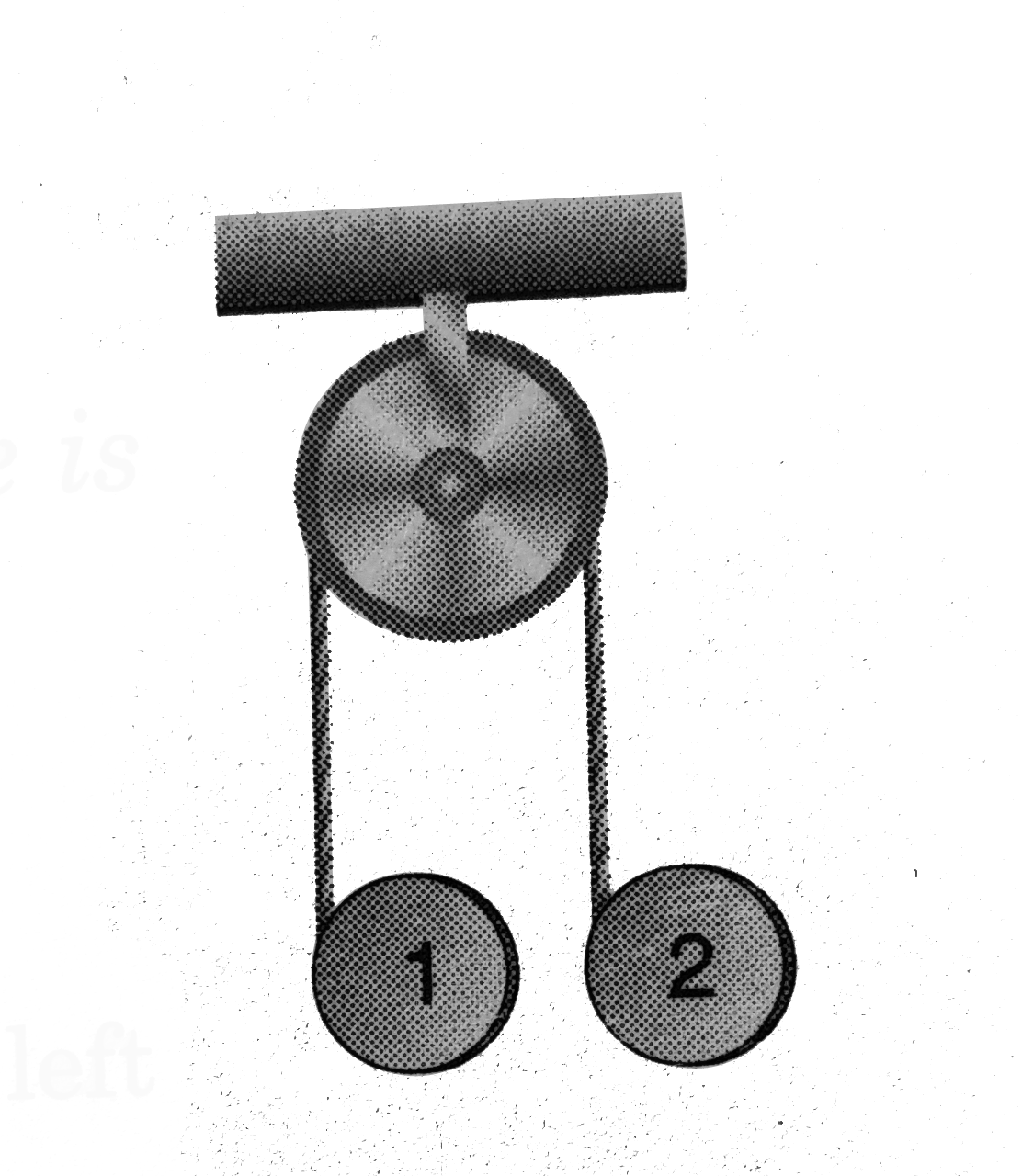
A thread is wound around two discs on either sides. The pulley and the two discs have the same mass and radius. There is no slipping at the pulley and no friction at the hinge. Find out the acceleration of the two discs and the angular acceleration of the pulley.View Solution The radius of gyration of an uniform rod of length L about an axis passing through its centre of mass and perpendicular to its length is.
View Solution