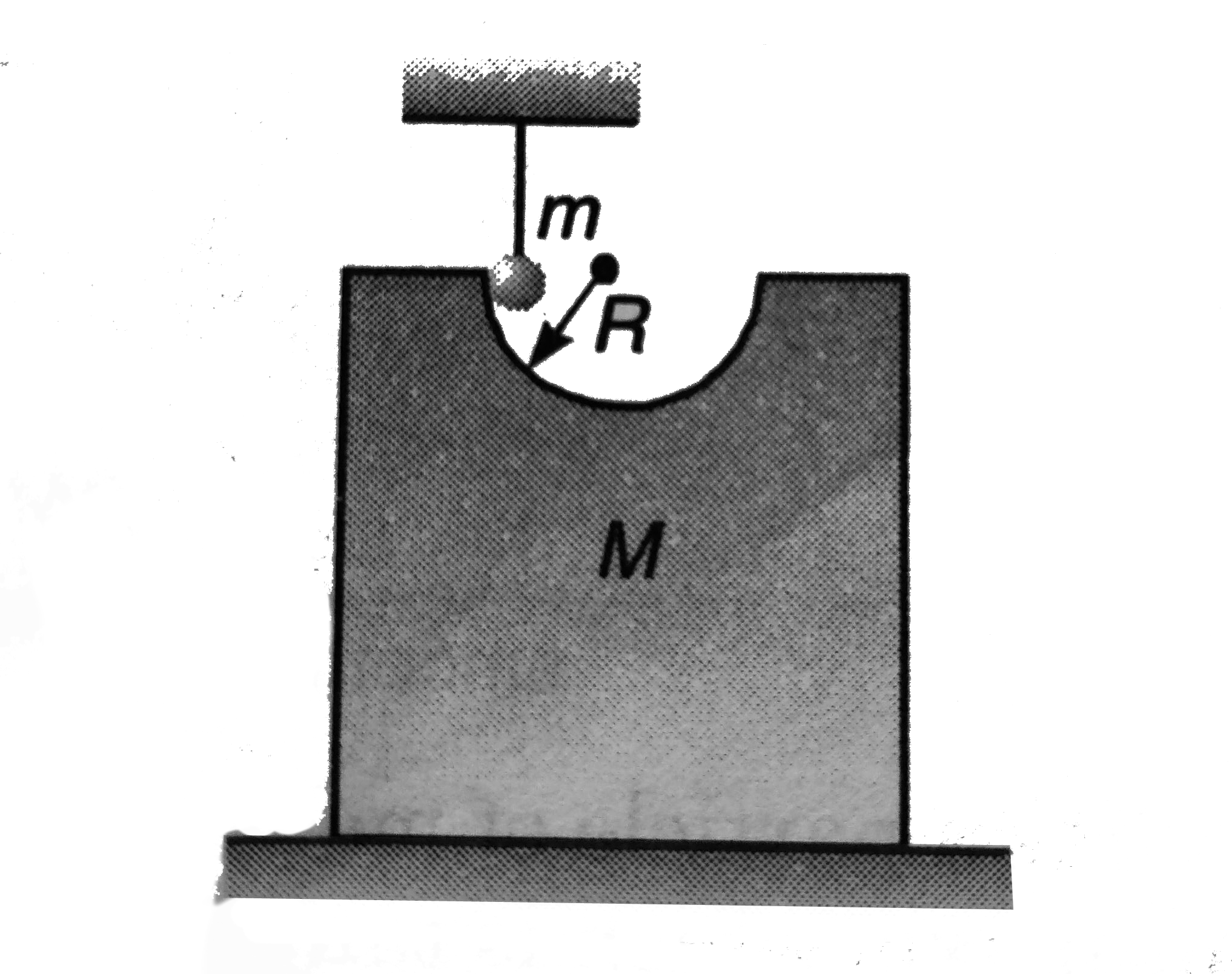
A semicircular track of radius R=62.5cm is cut in a block. Mass of block having track, is M=1kg and rests over a smooth horizontal floor. A cylinder of radius r=10cm and mass m=0.5kg is hanging by thread such that axes of cylinder and track are in same level and surface of cylinder is in contact with the track as shown in figure When the thread is burnt, cylinder starts to move down the track. Sufficient friction exists between surface of cylinder and track, so that cylinder does not slip.
Calculate velocity (in m/s) of the block when it reaches bottom of the track. (g=10m/s2)
The correct Answer is:2
Since block having semi circular track is over a smooth horizontal floor, therefore no horizontal reaction is provided by the floor or horizontal momentum of system of cylinder and block remains constant. But system is initially at rest or its initial horizontal momentum is zero. Therefore, horizontal momentum of the system always remains zero.
According to law of conservation of momentum
MV=mv or V=v2
Hence velocity of cylinder axis, relative to the block is
(v+V)=3v2(Right ward)
Angular velocity of cylinder is
ω(1.5v)r=15v (clockwise)
Moment of inertia of cylindder about its own axis is
I=mr22=2.5×10−3kgm2
Since cylinder does nopt slip over the track, therefore, there is no loss of energy due to friction.
Hence sum of KE of cylinder and block = Loss of PE of cylinder from top to bottom of the track
{12Iω2+12mv2}+12MV2=mg(R−r)
v=2m/s
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct
142 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions

A semicircular track of radius R=62.5cm is cut in a block. Mass of block having track, is M=1kg and rests over a smooth horizontal floor. A cylinder of radius r=10cm and mass m=0.5kg is hanging by thread such that axes of cylinder and track are in same level and surface of cylinder is in contact with the track as shown in figure When the thread is burnt, cylinder starts to move down the track. Sufficient friction exists between surface of cylinder and track, so that cylinder does not slip.
Calculate velocity of the block when it reaches bottom of the track. Also find force applied by block on the floor at that moment. (g=10m/s2)
View Solutionradius and height of a cylinder are 10cm and 10.5cm respectivey Find the surface area of the cylinder.
View Solution
Knowledge Check

A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k isA34MgsinθkB2MgsinθkCMgsinθkDnone of theseA 1000 kg car starts from rest at point 1 and moves without friction down the track as shown in the figure. At point 2, the radius od curvature of the track is 6m.
 Athe force exerted by the track on the car at point 2 is 4000 kg wtBthe force exerted by the track on the car at point 2 is 5000 kg wtCthe minimum safe value of the radius of curvature at point 3 is 15 mDthe minium safe value of the radius of curvature at point 3 is 10 m
Athe force exerted by the track on the car at point 2 is 4000 kg wtBthe force exerted by the track on the car at point 2 is 5000 kg wtCthe minimum safe value of the radius of curvature at point 3 is 15 mDthe minium safe value of the radius of curvature at point 3 is 10 mA block of mass M = 2 kg with a semicircular track of radius R = 1.1 m rests on a horizontal frictionless surface. A uniform cylinder of radius r = 10 cm and mass = 1.0 kg is released from rest from the top point A. the cylinder slips on the semicircular frictionless track. The speed of the block when the cylinder reaches the bottom of the track at B is (g=10ms−2)
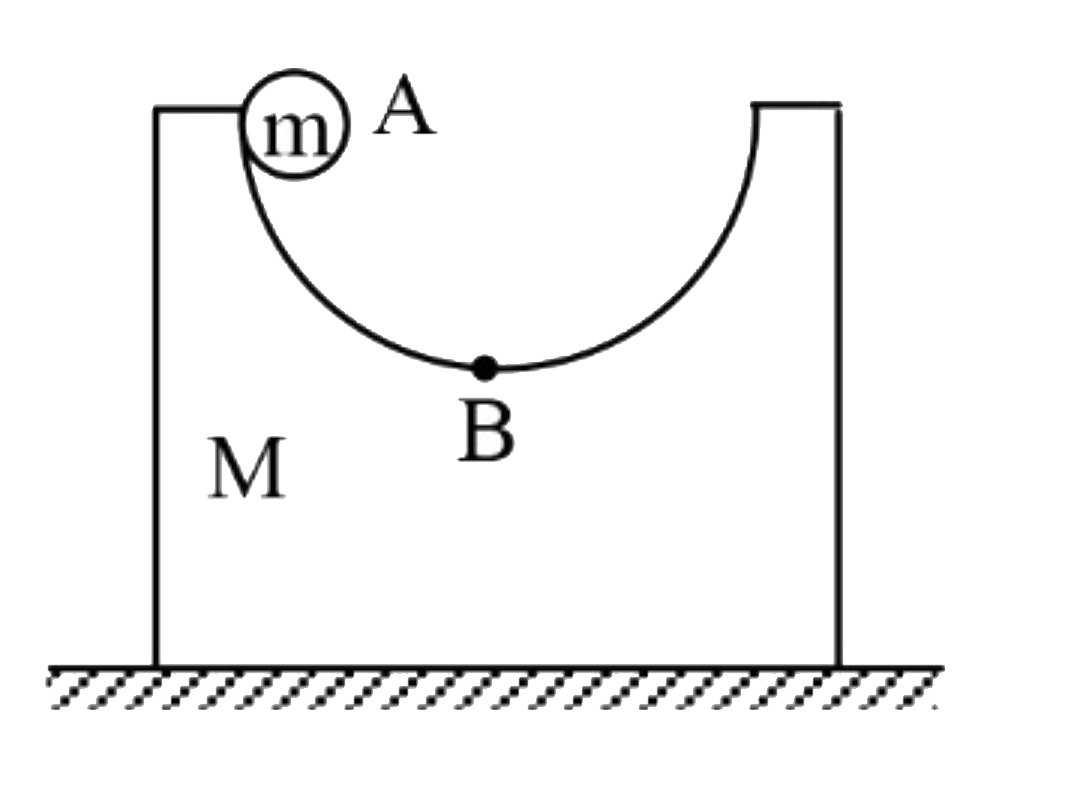 A√103ms−1B√43ms−1C√52ms−1D√10ms−1
A√103ms−1B√43ms−1C√52ms−1D√10ms−1
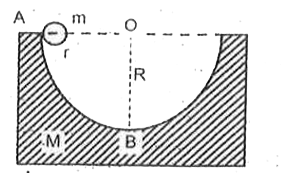
A block of mass M, with a semicircular track of radius R rest on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the point of the semicircular track. The cylinder slips in the semicircular frictionless track. How far the block moved when the cylinder reaches the bottom of the track ?
View SolutionA block of mass M with a semi circular track of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the top point A. The cylinder slips on the semicurcular frictionless track. How far has the block moved when the cylinder reaches the bottom of the track ? How fast is the block moving when the cylinder reaches the bottom of the track ?
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionA block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?

View SolutionCalculate the moment of inertia of a hollow cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder?
View Solution
