A series LCR circuit with L=0.12H,C=480nF, and R=23Ω is connected to a 230V variable frequency supply.
(a) What is the source frequency for which current amplitude is maximum? Find this maximum value.
(b) What is the source frequency for which average power absorbed by the circuit is maximum? Obtain the value of maximum power.
(c ) For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency?
(d) What is the Q-factor of the circuit?
Inductance, L=0.12H
Capacitance, C=480nF=480×10−9F
Resistance, R=23Ω
Supply voltage V=230V
Peak voltage is given as:
V0=√2×230=325.22V
Current flowing in the circuit is given by the relation,
Where,
I0= maximum at resonance
At resonance, we have
ωRL−IωgC=0
where,
ωR= Resonance angular frequency
∴ωR=1√LC
=1√0.12×480×10−9=4166.67 rad/s
∴ Resonant frequency, VR=ωR2π=4166.672×3.14=663.48Hz
And, maximum current (I0)max=V0R=325.2223=14.14A
(b) Maximum average power absorbed by the circuit is given as:
(Pas)ma x=12(I0)2MaxR
=12×(14.14)2×23=2299.3W
Hence, resonant frequ ency (VR) is 663.48Hz.
(c) The power tranferred to the circuit is h alf the powr at resonant frequency.
Freqeuncies at which power transferred is half, =ωR±Δω
=2π(VR±Δv)
where,
Δω=R2L
=232×0.12=95.83 rad/s
Hence, change in frequency, Δv=12πΔω=95.832π=15.26Hz
∴VR+ΔV=663.48+15.26=678.74Hz
And, vR−ΔV=663.48−15.26=648.22Hz
Hence, at 648.22Hz and 678.74Hz frequencies, the power transferred is half
At these frequencies, current amplitude can be given as:
I'1√2×(I0)Max
14.14√2=10A
(d) Q-factor of the gven circuit can be obtained using the relation Q=ωRLR
=4166.67×0.1223=21.74
Hence, the Q-factor of the given circuit is 21.74.
Topper's Solved these Questions
Similar Questions
A series LCR circuit with L=4.0H,C=100μF and R=60Ω is connected to a variable frequency 240 V source. Calculate
(i) angular frequency of the source which drives the circuit in resonance,
(ii) current at the resonating frequency,
(iii) rms potential drop across the inductance at resonance.View SolutionIf the frequency of the source e.m.f. in an AC circuit in n,the power varies with a frequency:
View Solution
Knowledge Check
- Question 1 - Select One
At resonant frequency the current amplitude in series LCR circuit is
AmaximumBminimumCzeroDinfinity - Question 2 - Select One
A series LCR circuit with R=20Ω,L=1.5H and C=35μF is connected to a variable frequency 200V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power in kW transferred to the circuit in one complete cycle?
A200 WB2000 WC100 WD4000 W - Question 3 - Select One
Figure shows a series LCR circuit connected to a variable frequency 230 V source.
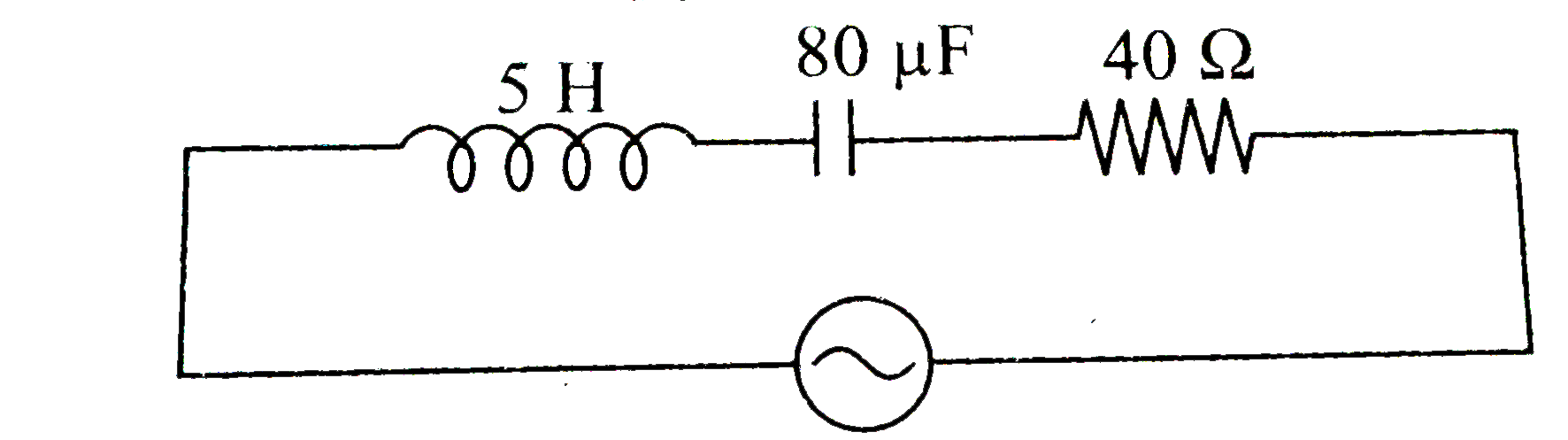
The source frequency which drives the circuit the circuit in resonance isA4 HzB5 HzC6 HzD8 Hz
A series L-C-R circuit with R = 20Ω, L = 1.5 H and C =35μF is connected to a variable frequency 200 V, AC supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transfered to the circuit, what is the average power transfered to the circuit in one complete cycle ?
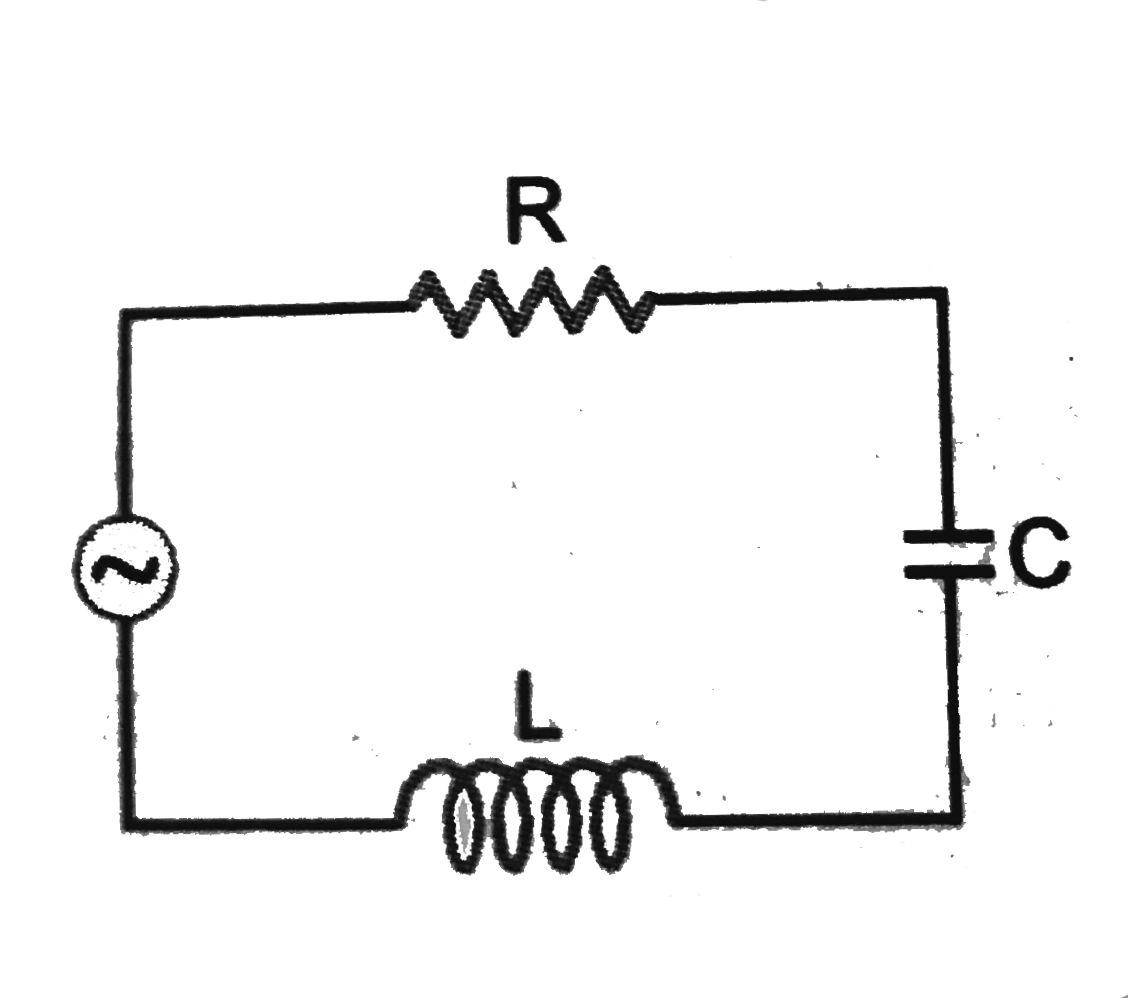
View SolutionFig. shows series LCR circuit with L=5.0H,C=80μF,R=40Ω connected to a variable frequency 240 V source. Calculate
(i) the angular frequency of the source which drives the circuit at resonance.
(ii) Current at the resonating frequency.
(iii) the rms pot. drop across the capacitor at resonance.
 View Solution
View SolutionPower delivered by the source of the circuit becomes maximum , when :
View SolutionA series LCR circuit with R=20Ω,L=1.5H and C=35μF is connected to a variable frequency 200V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power in kW transferred to the circuit in one complete cycle?
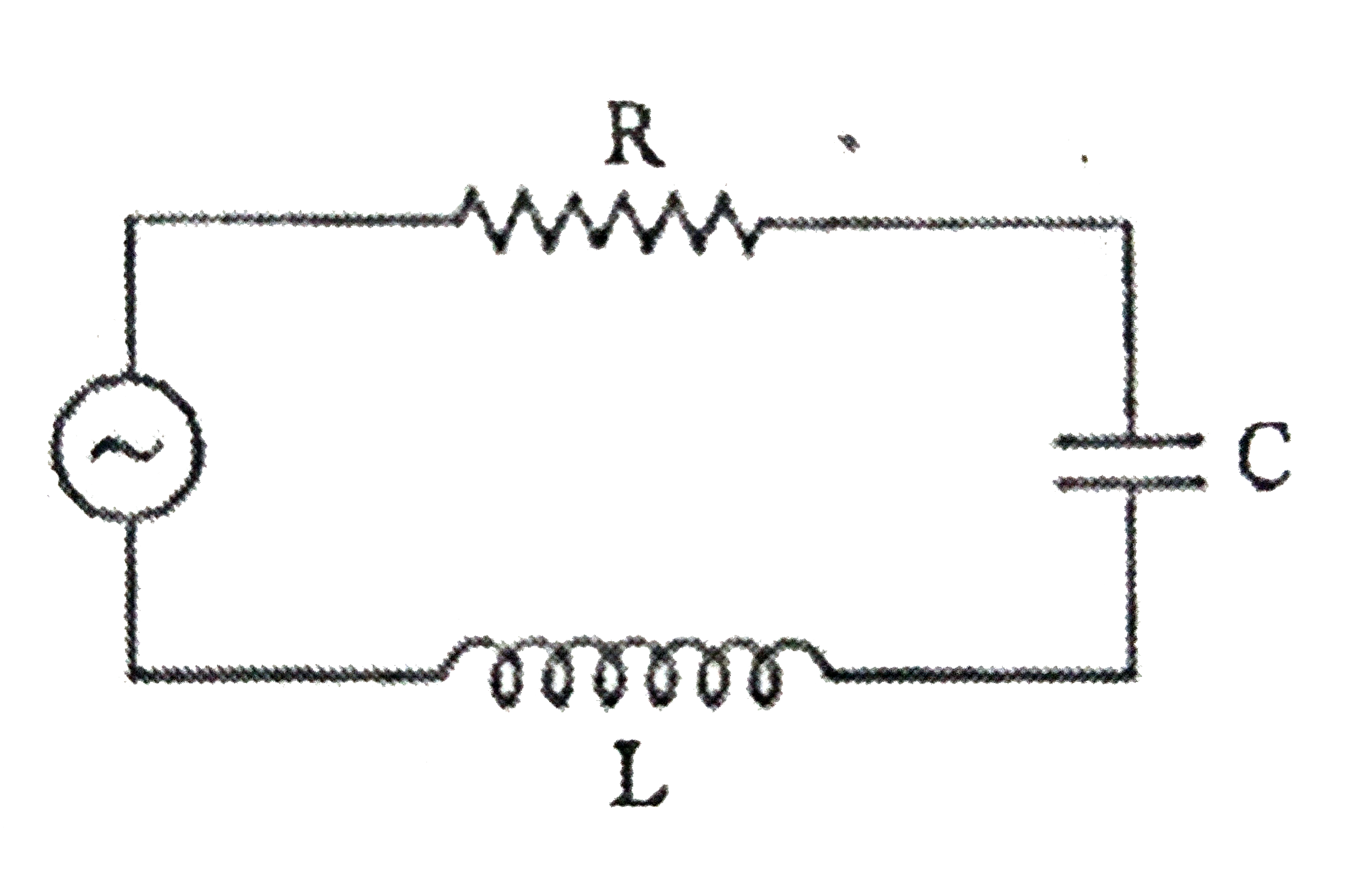
View SolutionThe figure shows a series LCR circuit with L=10.0H2,C=40μF,R=60Ω connected to a variable frequency 240 V source. Calculate
(i) The angular frequency of the source which drives the circuit at resonance.
(ii) The current at the resonating frequency.
(iii) The rms potential drop across the capacitor at resonance.
 View Solution
View Solution

