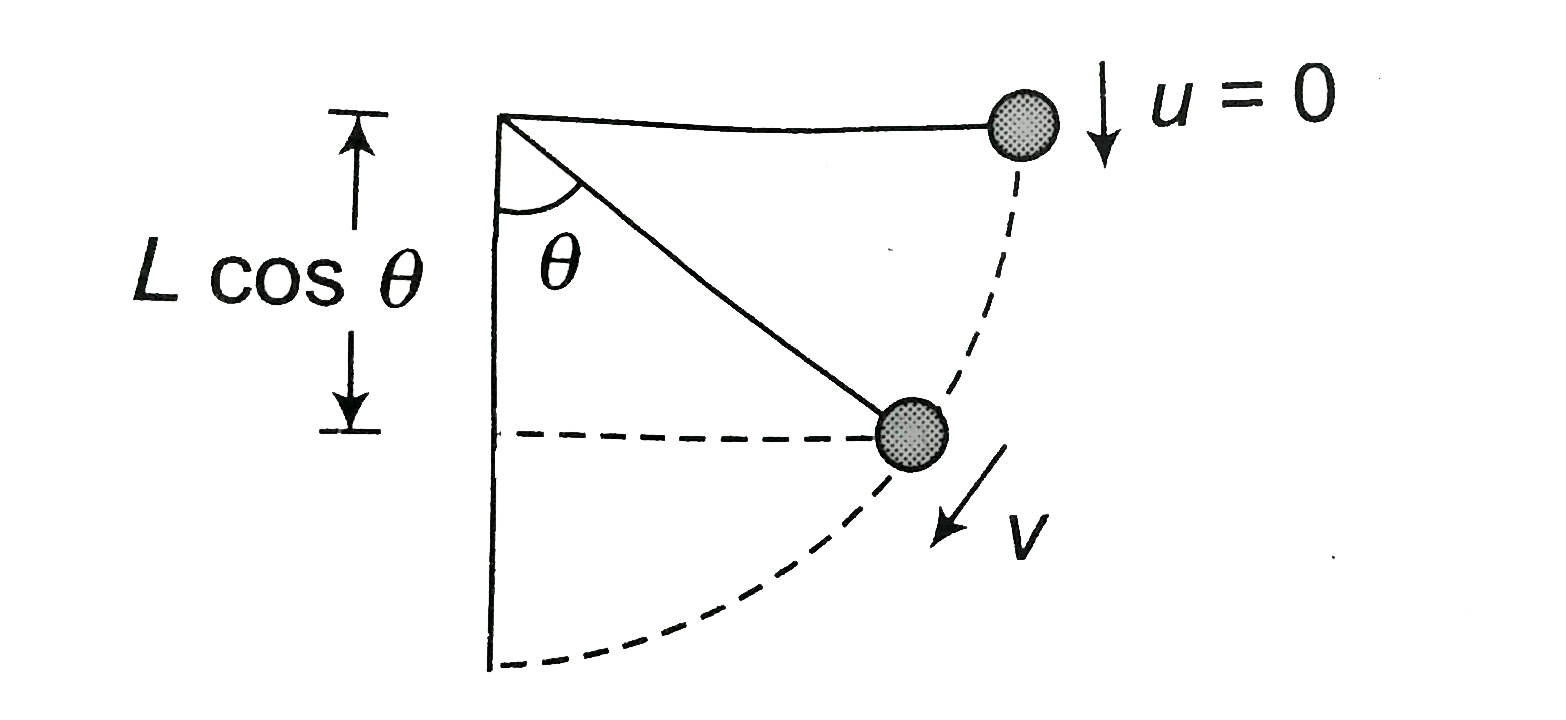
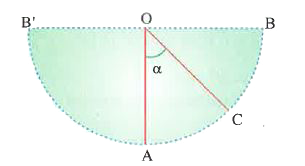
A simple pendulum is oscillating with an angular amplitude of 90∘ as shown in the figure. The value of θ for which the resulting acceleration of the bob is directed (i) vertically downward, (ii) vertically upward and (iii) horizontally is

90∘,0∘,sin−1(1/√3)
0∘,90∘,sin−1(1√3)
90∘,0∘,cos−1(1/√3)
0∘,90∘,cos−1(1/√3)
The correct Answer is:C
v2=2gLcosθ
ac=v2L=2gcosθ
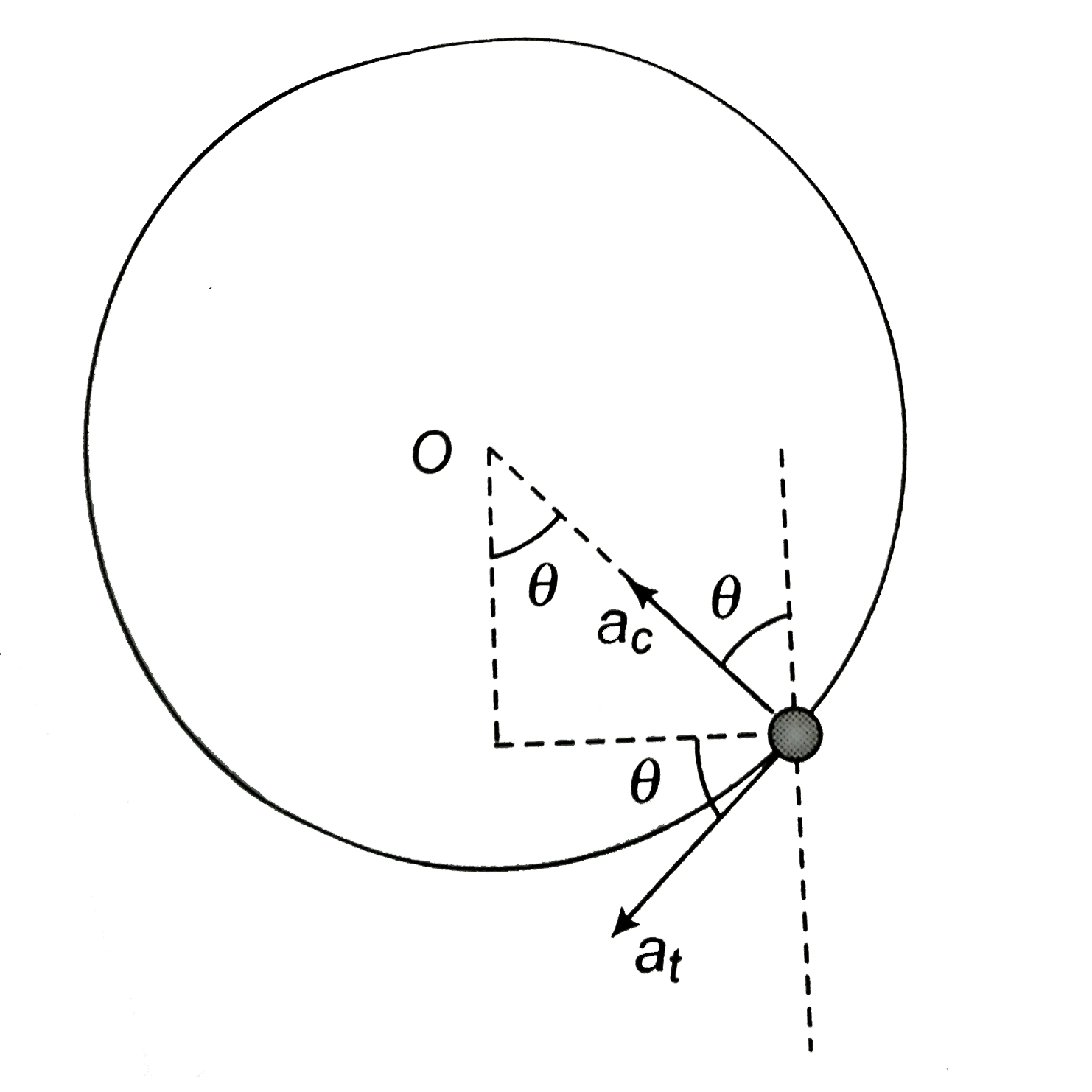
atgsinθ
since the acceleration is in the horizontal direction,
accosθ=atsinθ
2gcos2θ=gsin2θ
tan2θ=2⇒tanθ=√2
cosθ=1√3⇒θ=cos−1(1√3)
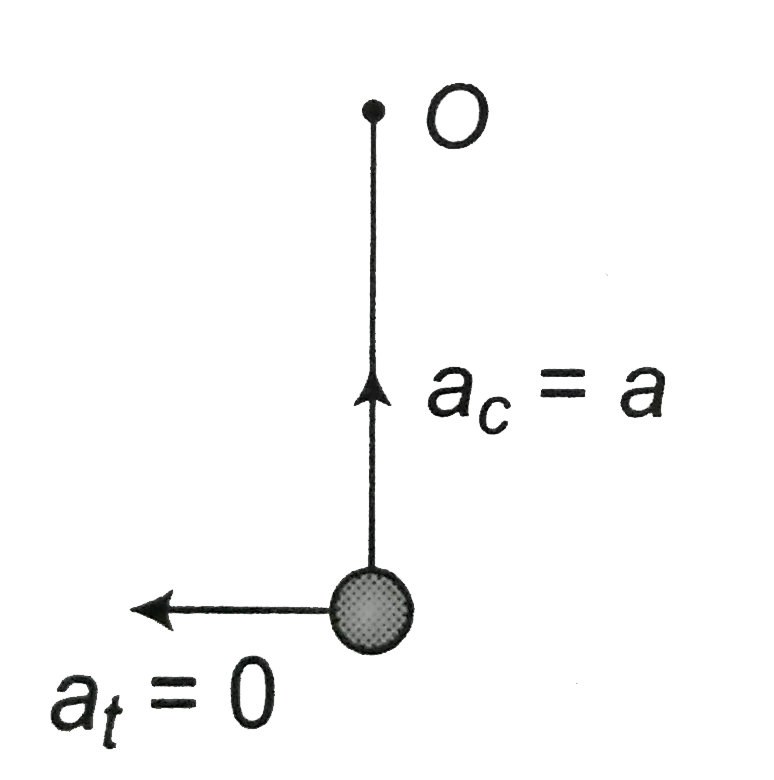
when θ=0, we have
total acceleration is vertically upward.
when θ=90∘, we have
total acceleration is vertically downward.
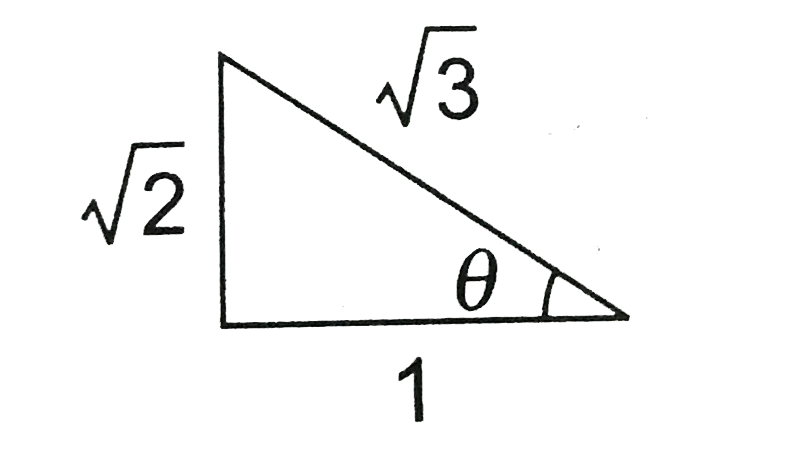
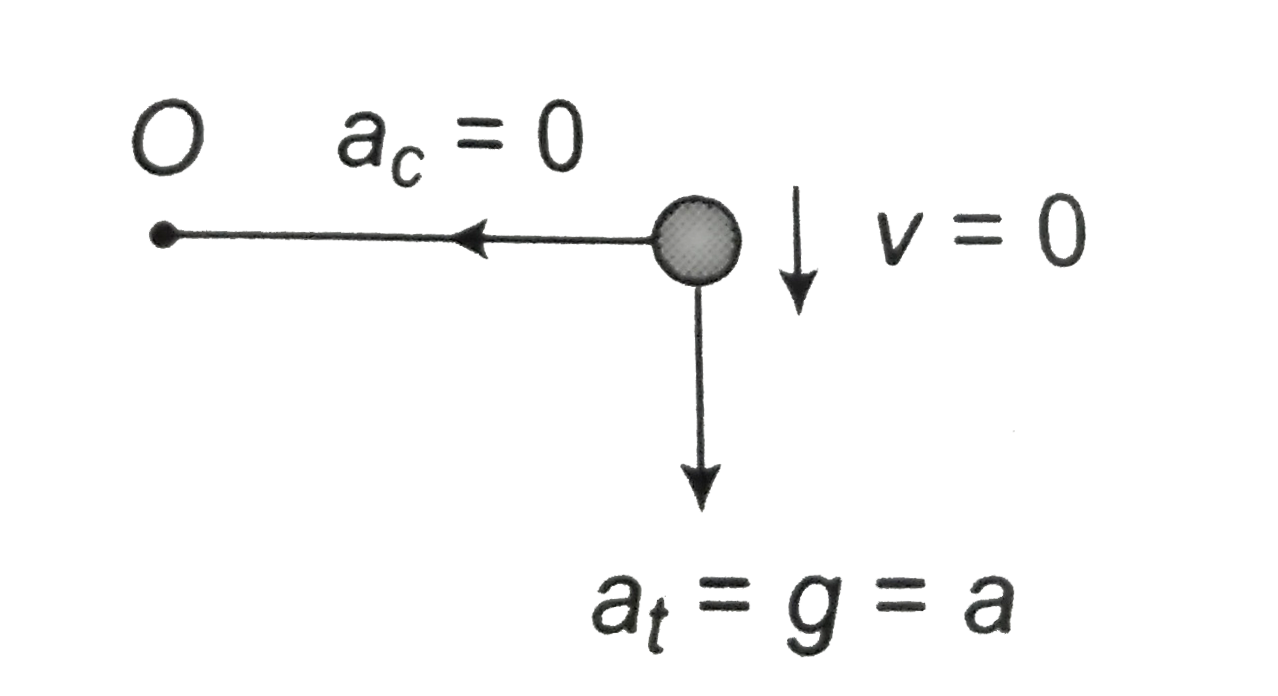
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A simple pendulum is vibrating with an angular amplitude of 90∘ as shown in the figure. For what value of a is the acceleration directed
i) vertically upwards
ii) horizontally
iii) vertically downwardA0∘,cos−1(1√3),90∘B90∘,cos−1(1√3),0∘Ccos−1(1√3),0∘,90∘Dcos−1(1√3),90∘,0∘ - Question 2 - Select One
A simple pendulum is vibrating with an angular amplitude of 90∘ as shown in figure. For what value of α (angle between string and vertical) during its motion, the total acceleration is directed horizontally ?
 Atan−1(12)Btan−1(1√2)Ccos−1(1/√3)Dsin−2(1/√3)
Atan−1(12)Btan−1(1√2)Ccos−1(1/√3)Dsin−2(1/√3) - Question 3 - Select One
A simple pendulum is oscillating with an angular amplitude 60∘. If mass of bob is 50 gram, then the tension in the string at mean position is (g=10ms−2)
A0.5 NB1 NC1.5 ND2 N
A second's pendulum is taken in a carriage. Find the period of oscillation when the carriage move s with an acceleration of 4ms−2 (i) vertically upwards (ii) vertically downwards, and (iii) in a horizontal direction.
View SolutionA second pendulum is takin in a carriage. Find the period of oscillation when the carriage moves with an acceleration of 4⋅2ms−2 (i) vertically upwards (ii) vertically downwards and (ii) in a horizontal direction.
View SolutionA simple pendulum oscillates with an anglular amplitude of θ. If the maximum tension in the string is 3 times the minimum tension, then the value of cosθ is
View SolutionA simple pendulum has a bob of mass m and swings with an angular amplitude ϕ. The tension in thread is T. At a certain time the string makes an angle θ with the vertical (θ≤ϕ)
View SolutionA simple pendulum swings with angular amplitude θ. The tension in the string when it is vertical is twice the tension in its extreme position. Then, cosθ is equal to
View Solution