A simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by the string of the pendulum with the vertical if this angle does not change during the turn. Take g=10ms2.
The correct Answer is:D
To solve the problem of finding the angle made by the string of a pendulum with the vertical when a car is taking a turn, we can follow these steps:
Step 1: Convert the speed from km/h to m/s
The speed of the car is given as 36 km/h. To convert this to meters per second (m/s), we use the conversion factor:
1 km/h=13.6 m/s
Thus,
36 km/h=363.6 m/s=10 m/s
Step 2: Calculate the centripetal acceleration
The centripetal acceleration ac can be calculated using the formula:
ac=v2r
where v is the velocity (10 m/s) and r is the radius of the turn (10 m). Therefore,
ac=(10)210=10010=10 m/s2
Step 3: Analyze the forces acting on the pendulum
When the car is turning, two forces act on the pendulum:
1. The gravitational force mg acting downward.
2. The centrifugal force mac acting horizontally outward (from the perspective of the car).
Step 4: Set up the relationship using trigonometry
Let θ be the angle made by the string with the vertical. The forces can be resolved into components:
- The vertical component is mg.
- The horizontal component is mac.
From the geometry of the situation, we can use the tangent function:
tan(θ)=acg
Substituting the values ac=10 m/s2 and g=10 m/s2:
tan(θ)=1010=1
Step 5: Solve for the angle θ
To find θ, we take the arctangent:
θ=tan−1(1)
This gives us:
θ=45∘
Final Answer
The angle made by the string of the pendulum with the vertical is 45∘.
---
The speed of the car is given as 36 km/h. To convert this to meters per second (m/s), we use the conversion factor:
1 km/h=13.6 m/s
Thus,
36 km/h=363.6 m/s=10 m/s
The centripetal acceleration ac can be calculated using the formula:
ac=v2r
where v is the velocity (10 m/s) and r is the radius of the turn (10 m). Therefore,
ac=(10)210=10010=10 m/s2
When the car is turning, two forces act on the pendulum:
1. The gravitational force mg acting downward.
2. The centrifugal force mac acting horizontally outward (from the perspective of the car).
Let θ be the angle made by the string with the vertical. The forces can be resolved into components:
- The vertical component is mg.
- The horizontal component is mac.
tan(θ)=acg
Substituting the values ac=10 m/s2 and g=10 m/s2:
tan(θ)=1010=1
To find θ, we take the arctangent:
θ=tan−1(1)
This gives us:
θ=45∘
The angle made by the string of the pendulum with the vertical is 45∘.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Question for short Answer
Explore 10 Videos
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Objective -2
Explore 6 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBook:HC VERMA ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONExercise:Objective -2
Explore 11 Videos
- FLUID MECHANICSBook:HC VERMA ENGLISHChapter:FLUID MECHANICSExercise:All Questions
Explore 90 Videos
Similar Questions
A pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Find the angle made by the string with the vertical.
View SolutionThe centripetal force required by a 1000 kg car that takes a turn of radius 50 m at a speed of 36 kmph is
View SolutionA pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Find the angle made by the string with vertical at equilibrium. Also find the tension in the sting in this position

View SolutionA simple pendulum of length 1 feet suspended from the ceiling of an elevator takes π3 seconds to complete one oscilation. Find the acceleration of the elevator.
View SolutionA 500 kg car takes a round turn of radius 50 m with a velocity of 36 km/hr . The centripetal force is
View SolutionA simple pendulum of length 5 m is suspended from the ceiling of a cart. Cart is sliding down on a frictionless surface having angle of inclination 60°. The time period of the pendulum is
View SolutionA seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4m/s2 . Its period of oscillation is
View SolutionA pendulum suspended from the ceiling of the train has a time period of two seconds when the train is at rest, then the time period of the pendulum, if the train accelerates 10 m/s2 will be (g=10m/s2)
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
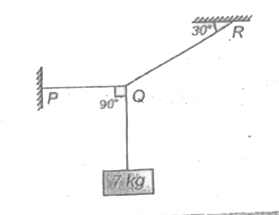
View SolutionThe angle made by the string of a simple pendulum with the vertical depends on time as θ=π90sin[(πs−1)t]. Find the length of the pendulum if g=π2ms−2
View Solution