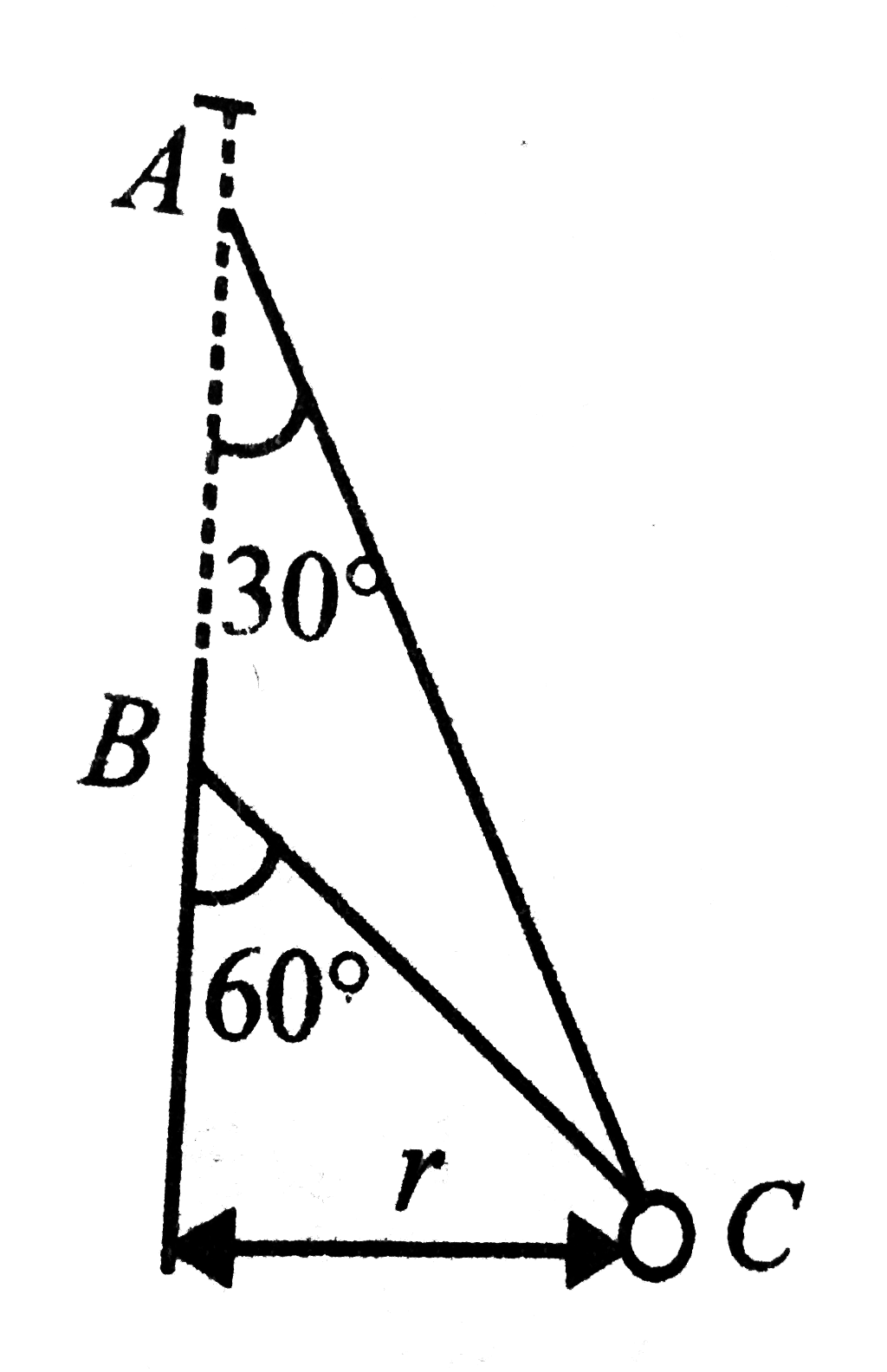
A single wire ACB passes through a smooth ring at C which revolves at a constant speed in the horizontal circle of radius r as shown in the fig. the speed of revolution is

√rg
√2rg
2√2rg
2√rg
The correct Answer is:1
Tcos60∘+Tcos30∘=mv2R
Tcos30∘+Tcos60∘=mg
v=√rg
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A single wire ACB passes through a smooth ring at C which revolves at a constant speed in the horizontal circle of radius r as shown in the figure. The speed of revolution is √yrg6. Find y.
'(##CEN_KSR_PHY_JEE_C07_015_Q09##)'View SolutionA single wire ACB passes through a smooth ring at C when revolves at a constant speed in the horizontal circle of radius r=6.4m as shown in the figure. Find the speed (in m/s) of revolution of the ring.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two wires AC and BC are tied at C of a small sphere of mass 5kg, wheich revolves at a constant speed v in the horizontal speed v in the horizontal circle of radius 1.6m. Find the minimum value of v
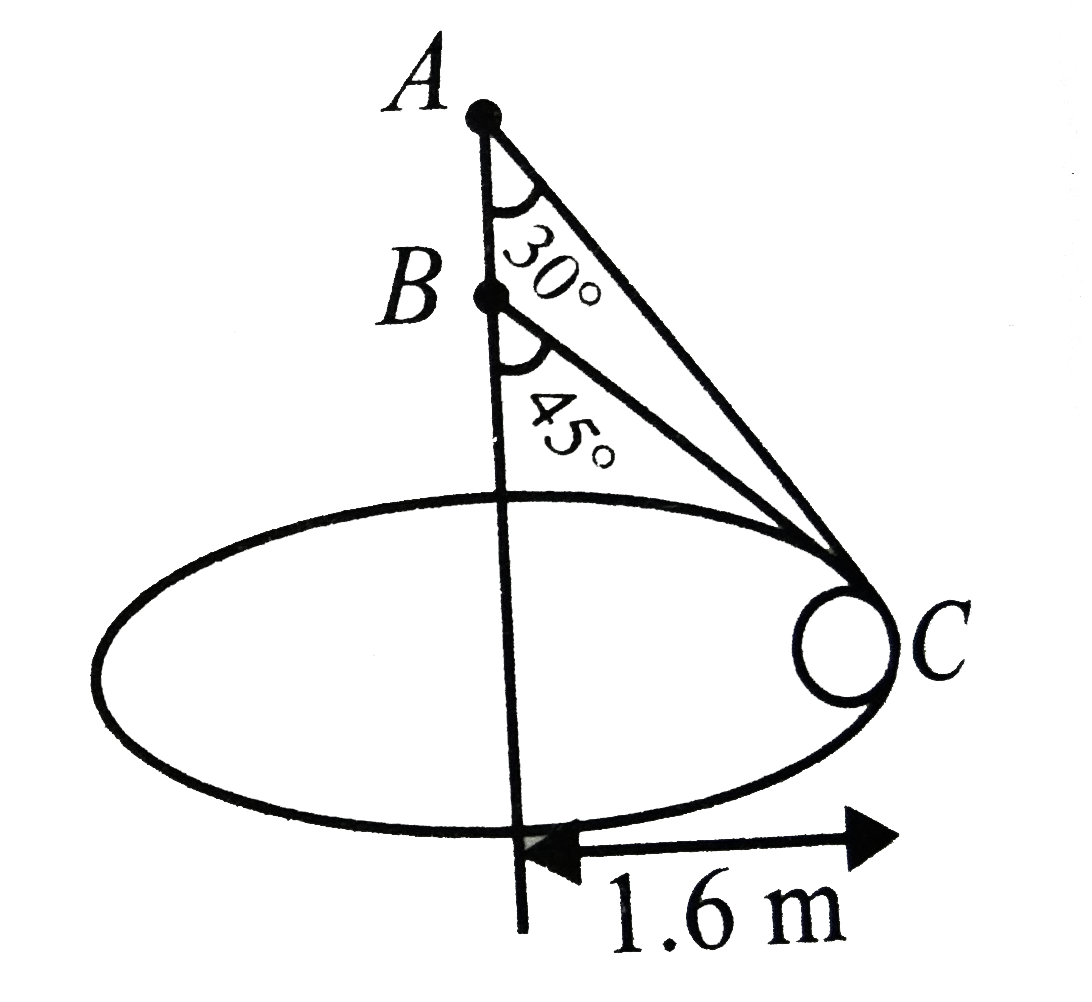 A4ms−1B2ms−1C2.5ms−1Dnone of these
A4ms−1B2ms−1C2.5ms−1Dnone of these - Question 2 - Select One
For a body moving with constant speed in a horizontal circle , which of the following remains constant ?
AvelocityBaccelerationCCentripetal forceDKE - Question 3 - Select One
Under the influence of a uniform magnetic field, a charged particle moves with constant speed v in a circle of radius r. The time period of revolution of the particle
Adepends on v and not on rBdepends on r and not on vCis independent of both v and rDdepends on both v and r
Two wires ACandBC are tied at C of small sphere of mass 5kg which revolves at a constant speed v in the horizontal circle of radius 1.6m Find the maximum value of v
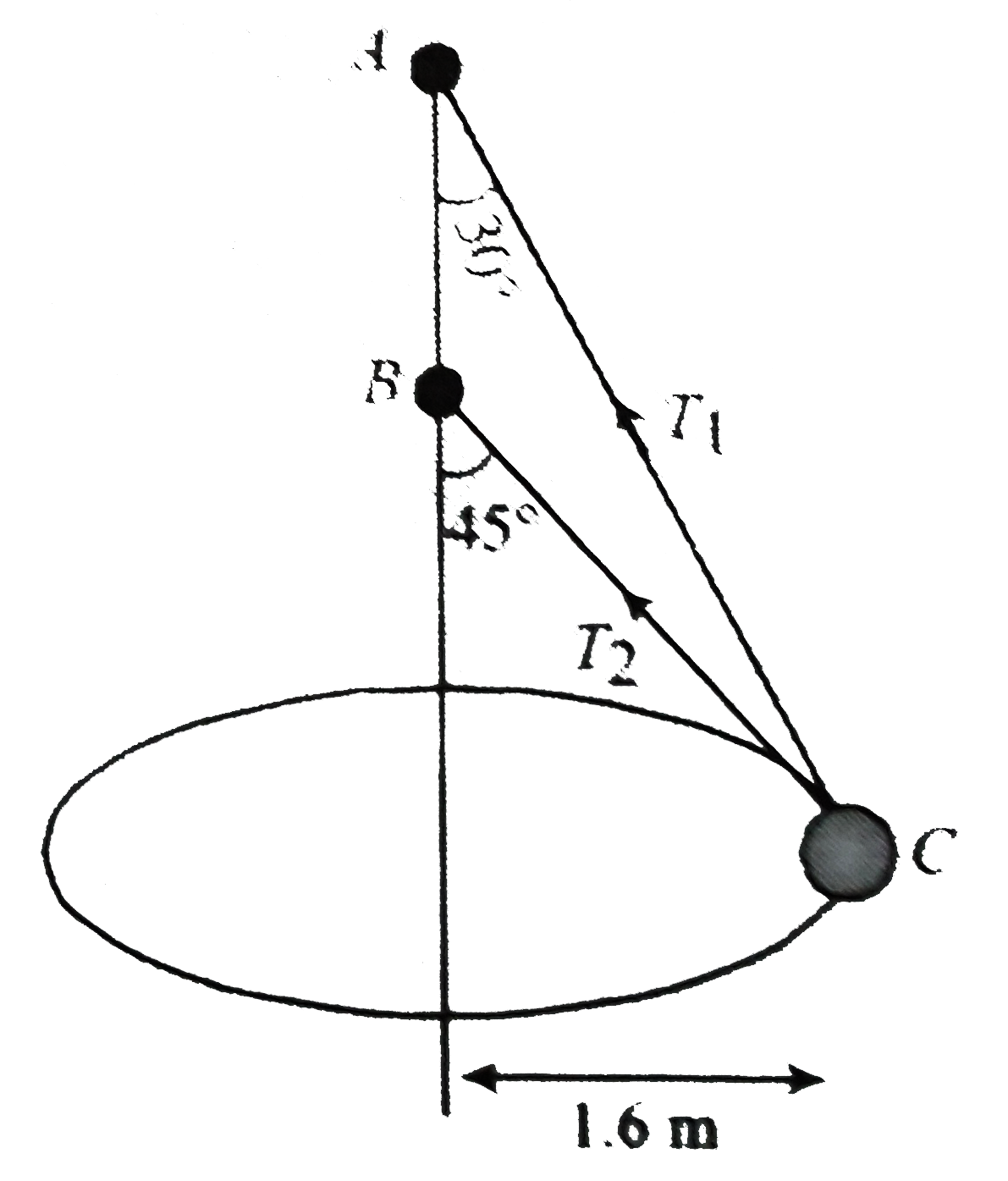 View Solution
View SolutionA body of mass 0.4 kg is whirled in a horizontal circle of radius 2 m with a constant speed of 10ms−1. Calculate its frequency of revolution.
View SolutionA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are
 View Solution
View SolutionIf a particle covers half the circle of radius R with constant speed then
View SolutionA particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
View Solution

