A skier plane to ski a smooth fixed hemisphere of radius R . He starts from rest from a curve smooth surface of height (R4) . The angle θ at which he leaves the hemisphere is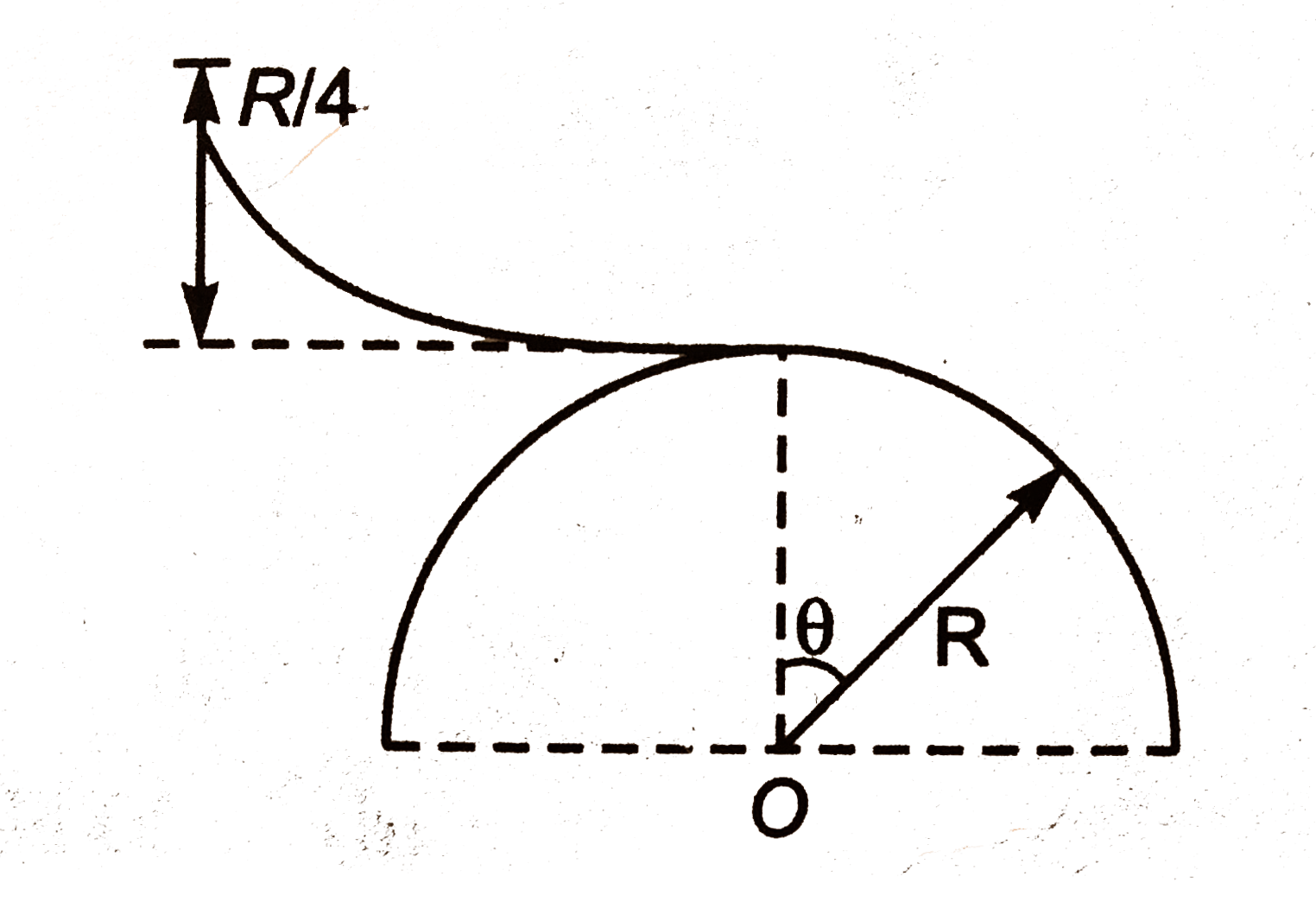 
cos−1(23)
cos−1(5)√3
cos−1(56)
cos−1[52√3]
The correct Answer is:C
At the time of leaving contact
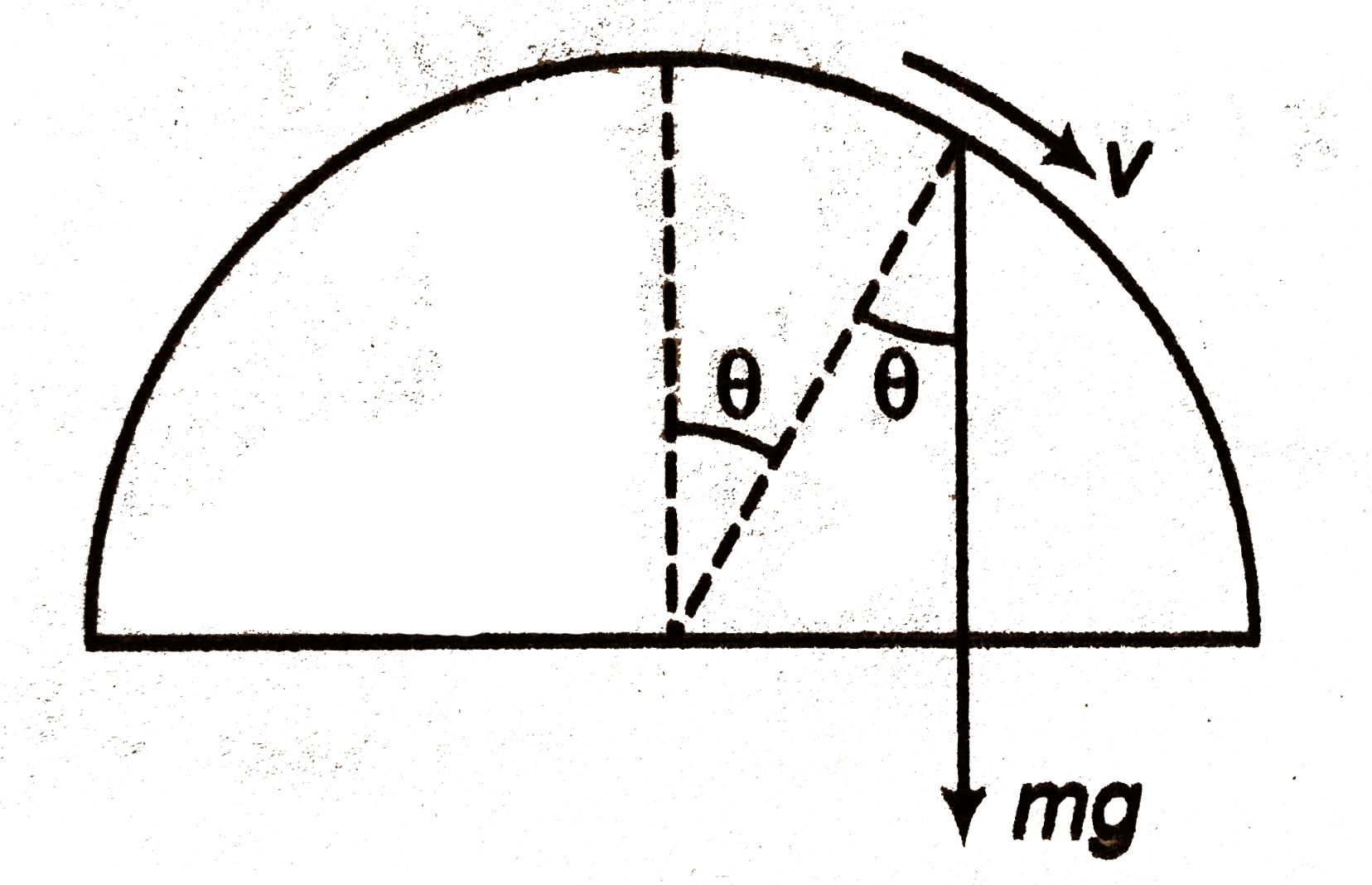
N=0
:. mgcosθ=mv2R=m(2gh)R
:. cosθ=2hR=[R4+R(1−cosθ)]R
On solving this equation, we get
cosθ=5/6 or θ=cos−1(56)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct5videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based5videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Subjective13videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
A small block of mass m projected horizontally from the top of the smooth and fixed hemisphere of radius r with speed u as shown. For values of u≥u0(u0=√gr) it does not slide on the hemisphere. l i.e., leaves the surface at the top itself.
For u=u0/3, Find the height from the ground at which it leaves the hemisphereView SolutionA particle of mass m is placed in equilibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical where cosθ=35. if the work done against friction is 2mgR10x, find x.
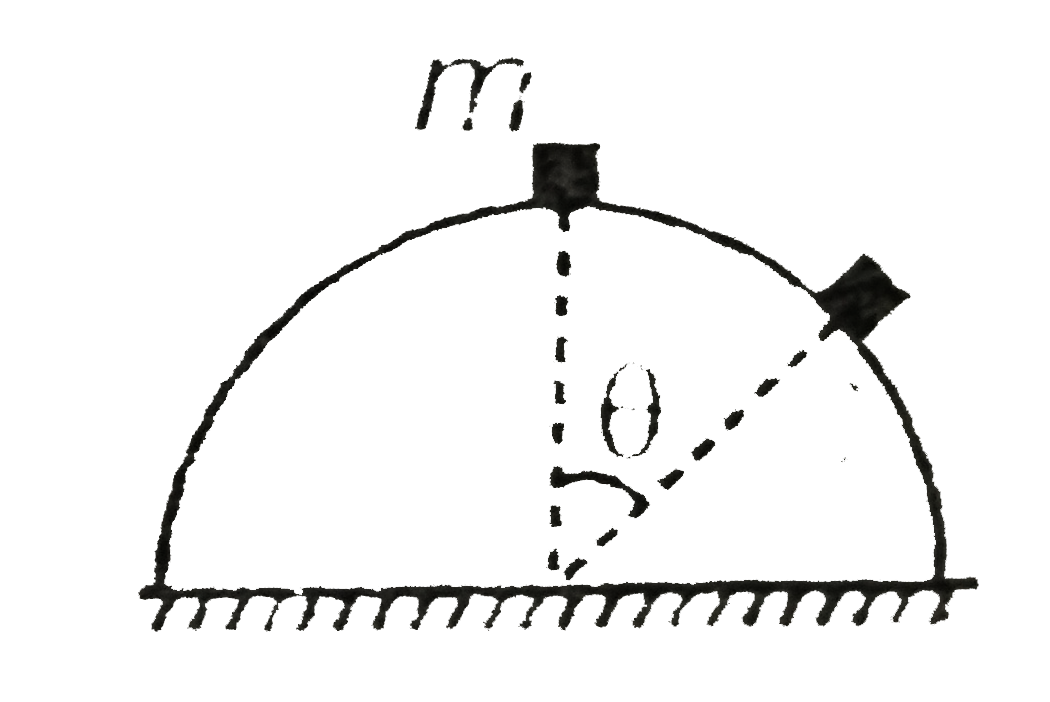View Solution
Knowledge Check
- Question 1 - Select One
A particle rests on the top of a hemishpere of radius R. Find the smallest horizontal velocity that must be imparted to the particle if it is yo leave the hemisphere without sliding down it.
A√gRB√2gRC√3gRD√5gR
A small block of mass m projected horizontally from the top of the smooth and fixed hemisphere of radius r with speed u as shown. For values of u≥u0(u0=√gr) it does not slide on the hemisphere. l i.e., leaves the surface at the top itself.
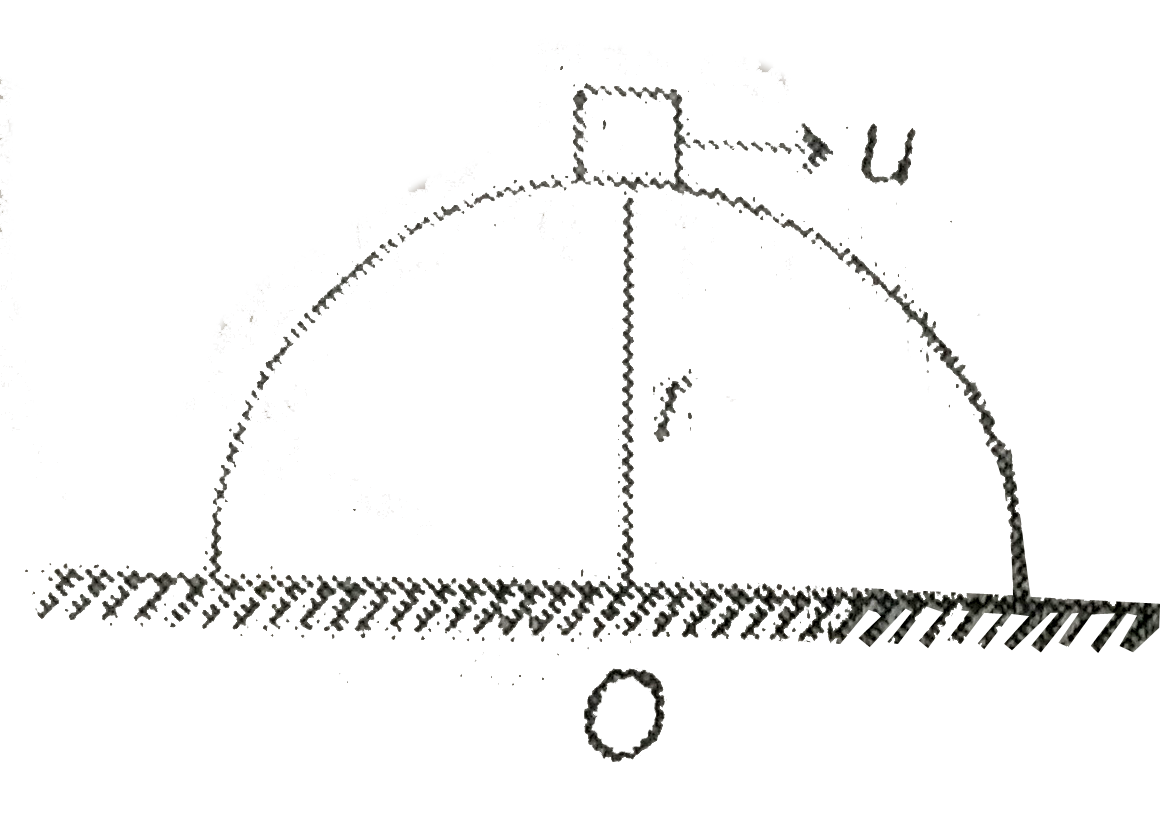
In the above problem find its net acceleration at the instant it levels the hemisphere.View SolutionA small block of mass m projected horizontally from the top of the smooth and fixed hemisphere of radius r with speed u as shown. For values of u≥u0(u0=√gr) it does not slide on the hemisphere. l i.e., leaves the surface at the top itself.
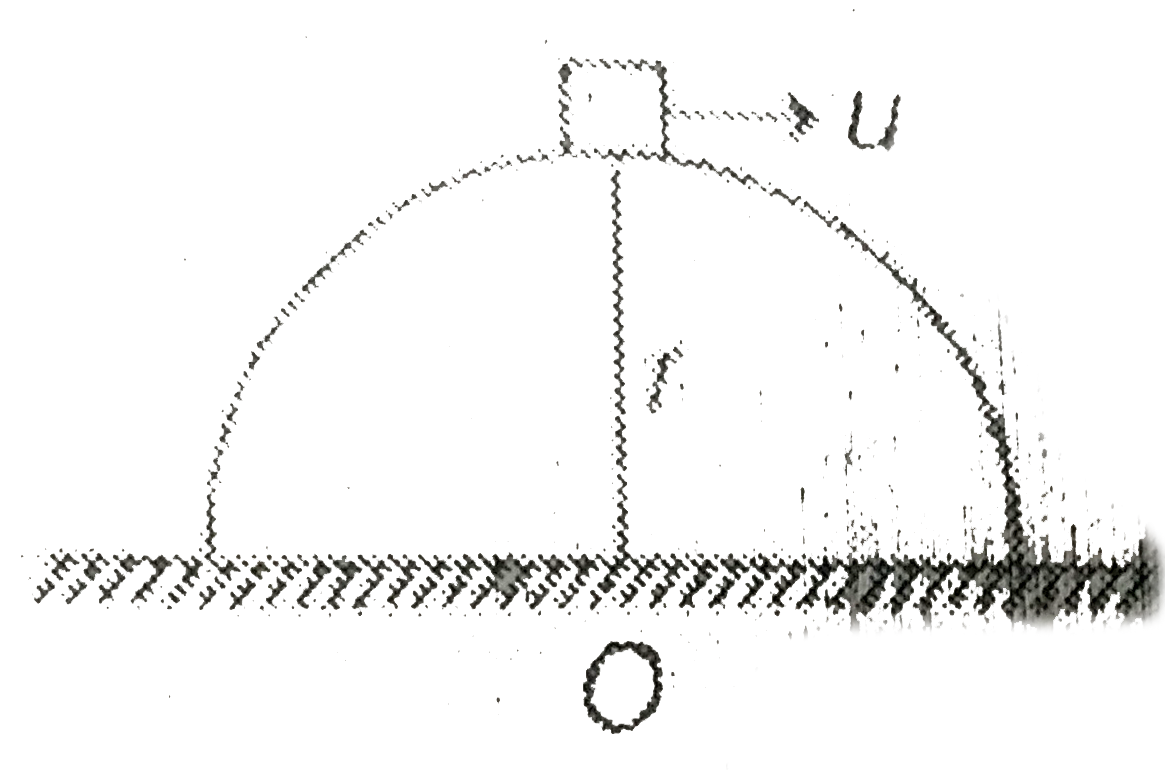
For u=2u0, it lands at point P on ground. Find OP.View SolutionA particle rests on the top of a smooth hemisphere of radius r. It is imparted a horizontal velocity of √ηgr. Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.
View SolutionA block of mass m moving on a fixed smooth hemisphere of rudius R. If speed of block at top most point of the hemisohere is √gR as shown in the figure, then the angle (θ) with the vertical, where the normal contact force becomes zero will be
View SolutionA small block of mass m has speed√gR2 at the top most point of a fixed hemisphere of radius R as shown in figure. The angle θ, when block loses the contact with the hemisphere is
_PHY_E05_149_Q01.png)
View SolutionA particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is μ=1√3. The maximum height up to which the particle can remain stationary is
View SolutionA small solid sphere of mass m and radius r starting from rest from the rim of a fixed hemispherical bowl of radius R(>>r) rolls inside it without sliding. The normal reaction exerted by the sphere on the hemisphere when it reaches the bottom of hemisphere is
View Solution