A small section of area ΔA is removed from a uniform spherical shell with surface mass density σ and radius R as shown in the figure . Find the magnitude of gravitational field intensity at point P due to the remaining mass .

4σΔAG9R2
4σΔAGR2
σΔAGR2
zero
The correct Answer is:A
Step by step video & image solution for A small section of area DeltaA is removed from a uniform spherical shell with surface mass density sigma and radius R as shown in the figure . Find the magnitude of gravitational field intensity at point P due to the remaining mass . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A tunnel has been dug into a solid sphere of non-uniform mass density as shown in the figure. As one moves from A to B, the magnitude of gravitational field intensity

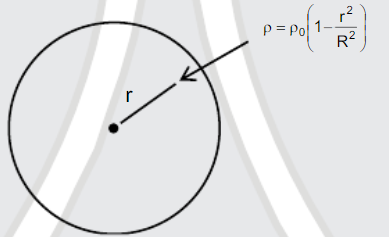
View SolutionMass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionA small area is removed from a uniform spherical shell of mass M and radius R. Then the gravitatioinal field intensity near the hollow portion is
View SolutionTwo concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is

View SolutionA spherical hole is made in a solid sphere of radius R. The mass of the sphere before hollowing was M. The gravitational field at the centre of the hole due to the remaining mass is

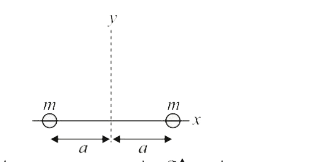
View SolutionTwo identical spherical balls, each of mass m, are placed as shown in figure. Plot the variation of g(gravitation intensity) along the x-axis due to both the masses.
View SolutionA disc of mass m and radius R is rolling without slipping as shown in the figure. The magnitude of net velocity of the point P is (OP=R2)
View SolutionTwo concentric speherical shells are as shown in figure. The magnitude of gravitational potential (V) and field strength (E ) vary with distance ( r) from centre as

View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View Solution
