
A small solid sphere of mass m is released from point A. portion AB is sufficiently rough (to provide accelerated pure rolling) BC is smooth and after C the ball moves freely under gravity find gravitational potential energy (U), rotational kinetic energy (KR) ad translational kinetic energy (KT) at points A, B, C , D and E.
AB, is sufficient rough BC is smooth and after C motion is under gravity. So, total mechanical energy (U+KR+KT) is always constant. On AB:
KRKT=25 (for solid sphere)
as accelerated pure rolling is taking place.
After B, rotational kinetic enerrgy will becom constant, after C centre of the ball will follow a projectile motion.
∴vD=vCcos60∘=vC2= half of vC
∴(KT)D=14(KT)C
At point A
U=3mgh
KR=0⇒KT=0
∴ mechanical energy E=3mgh= constant
At point B
U=0⇒E=3mgh
∴K=E=3mgh
but KRKT=25
∴KR=27K=67mgh
KT=57K=157mgh
At point C
U=mgh
KR=(KR)B=67mgh
KT=E−U−KR
=3mgh−mgh−67mgh=86mgh
At point D
KR=(KR)B=67mgh
KT=14(KT)C=27mgh
U=E−KR−KT
=3mgh−67mgh−27mgh
=137mgh
At point E
U=0
KR=(KR)B=67mgh
KT=E−KR−U
=3mgh−67−0=156mgh
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A rod of mass m spins with an angular speed ω=√gl, Find its a. kinetic energy of rotation. b. kinetic energy of translation c. total kinetic energy.

View SolutionA rod of mass m and length l is connected with a light rod of length l. The composite rod is made to rotate with angular velocity ω as shown in the figure. Find the
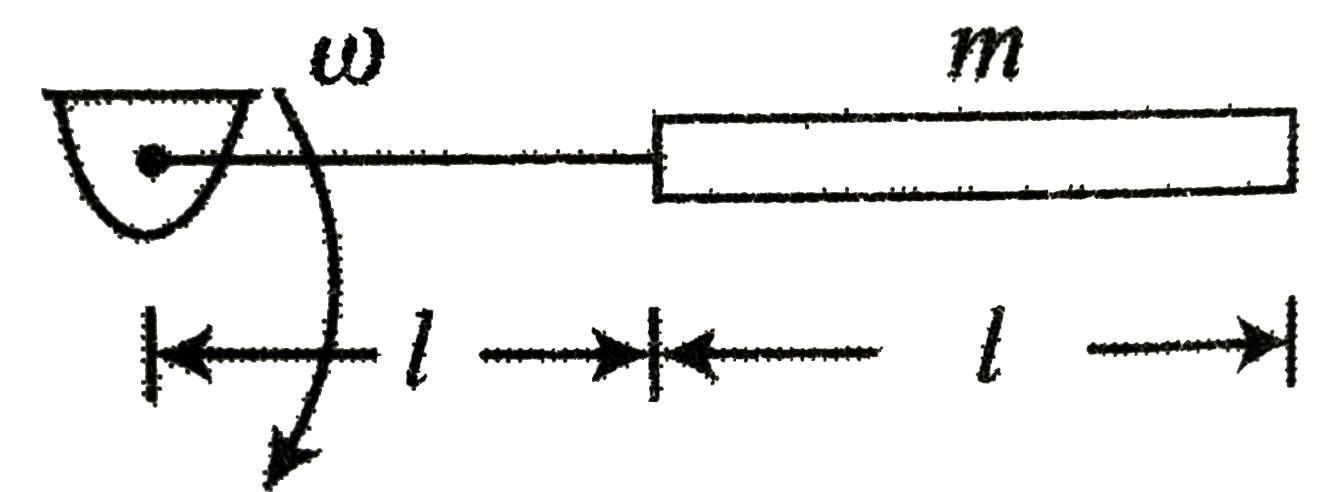
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.
View Solution
Knowledge Check
A solid sphere is in rolling motion. In rolling motion a body prosseses translational kinetic energy (Kt) as well as rotational kinetic energy (Kr) simutaneously. The ratio
Kt:(Kt+Kr) for the sphere isA10:7B2:5C5:7D7:10A solid sphere is in rolling motion . In rolling motion a body possesses translational kinetic energy (Kt) as well as rotational kinetic energy (Kr) simultaneously . The ratio Kt:(Kt+Kr) for the sphere is
A7:10B5:7C10:7D2:5Portion AB of the wedge shown in figure is rough and BC is smooth. A solid cylinder rolld without slipping from A to B. Find the ratio of translational kinetic energy to rotationa linetic energy, when the cylinder reaches point C.
 .A3/5B5C7/5D8/3
.A3/5B5C7/5D8/3
Portion AB of the wedge shown in figure is rough and BC is smooth. A solid cylinder rolld without slipping from A to B. Find the ratio of translational kinetic energy to rotationa linetic energy, when the cylinder reaches point C.
 .
.
View SolutionA solid sphere of mass m and radius R rolls without slipping on the horizontal surface such that its velocity of center of mass is v0. Find its translational kinetic energy, rotational kinetic energy, total kinetic energy, gravitational potential energy taking surface as reference level and mechanical energy.
View SolutionA small steel sphere of mass m and radius r rolls without slipping on the fiictionless surface of a large hemisphere of radius R{R gt gt r) whose axis of symmetry is vertical. It starts at the top from the rest, (a) What is the kinetic energy at the bottom ? (b) What fraction is the rotational kinetic energy of the total kinetic energy at the bottom? (b) What fraction is the rotational kinetic energy of the total kinetic energy? (c) What fraction is the translational kinetic energy of the total kinetic energy? (d) Calculate the normal force that the small sphere will exerton.the hemisphere at its bottom. Howthe results will be affected if r is not very sjnall as compared to R.
View SolutionPortion AB of the wedge shown in figure is rough and Bc is smooth. A solid cylinder rolls without spinning from A to B. If AB=BC, then ratio of transitional kinetic energy to rotational kinetic energy, when the cylinder reaches point C is

View SolutionA rolling body is released from rest on sufficient rough long inclined plane of inclination θ. Consider four points A, B, C and D on the sphere. After one revolution.
View Solution
