A smooth square plateform ABCD is moving towards right with a uniform speed v. At what angle θ must a particle be projected from A with speed u so that it strikes the point B
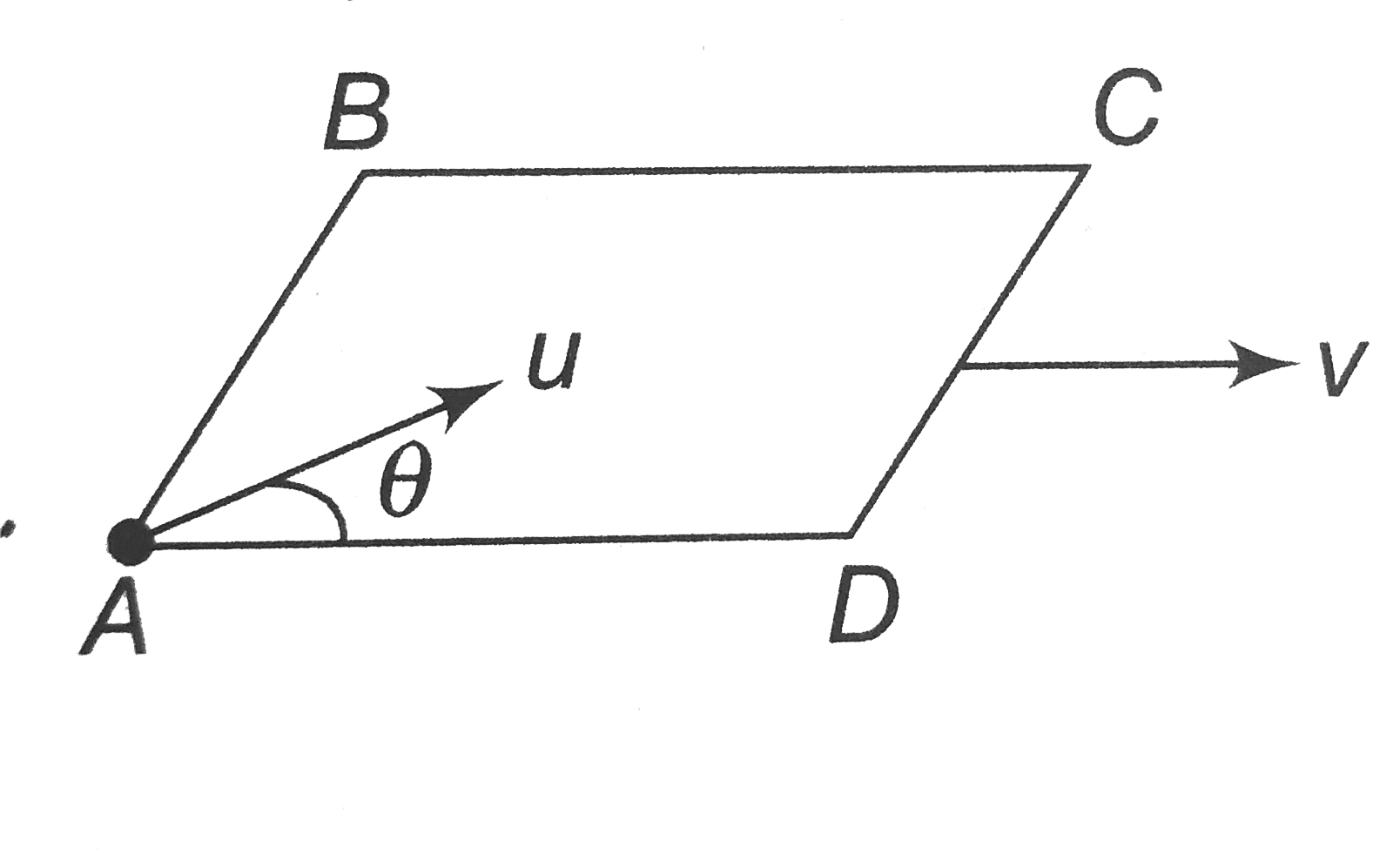
sin−1(uv)
cos−1(vu)
cos−1(uv)
sin−1(vu)
The correct Answer is:b
At t=18×2πω=π4ω
x-coordinate of P=ωR(π4)>Rcos45∘
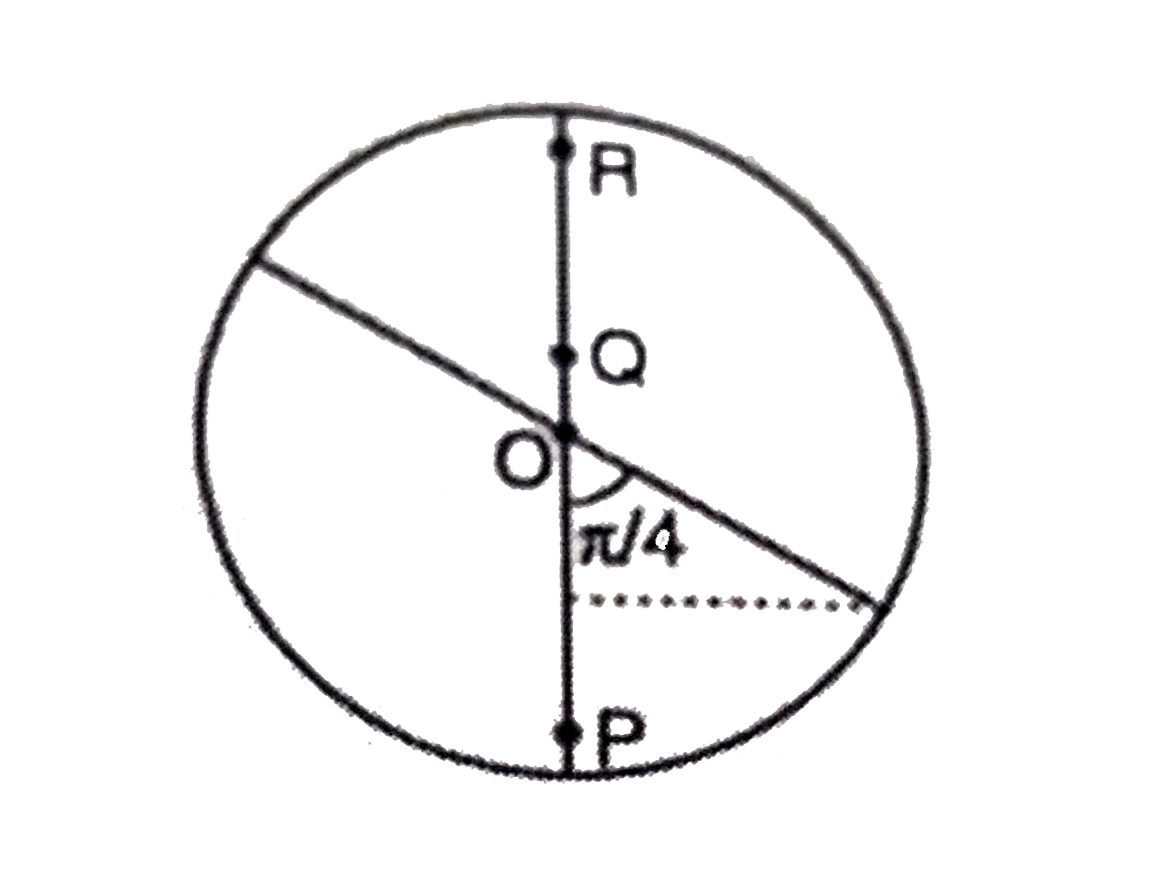
Therefore, both particle P and Q land in unshaded region.
Topper's Solved these Questions
Similar Questions
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution. If this particle were projected with the same speed at an angle θ to the horizontal, the maximum height attained by it equals 4R. The angle of projection θ is then given by
View SolutionA large wedge BCD, having its inclined surface at an angle θ=45∘ to the horizontal, is travelling horizontally leftwards with uniform velocity u=10m/s
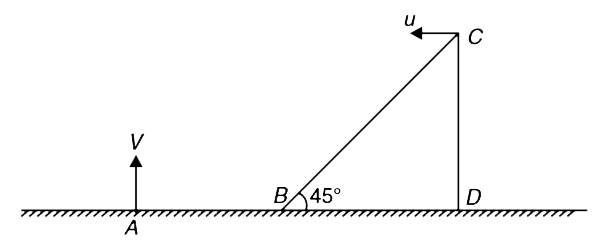
At some instant a particle is projected vertically up with speed V=20m/s from point A on ground lying at some distance right to the lower edge B of the wedge. The particle strikes the incline BC normally, while it was falling. [g=10m/s2]
(a) Find the distance AB at the instant the particle was projected from A.
(b) Find the distance of lower edge B of the wedge from point A at the instant the particle strikes the incline.
(c) Trace the path of the particle in the reference frame attached to the wedge.
View Solution
Knowledge Check
A smooth square platform ABCD is moving towards right with a uniform speed v. At what angle θ must a particle be projected from A with speed u so that it strikes the point B
 Asin−1(uv)Bcos−1(vu)Ccos−1(uv)Dsin−1(vu)
Asin−1(uv)Bcos−1(vu)Ccos−1(uv)Dsin−1(vu)A particle is projected at an angle θ from ground with speed u (g = 10 m/s2 )
Aif u = 10 m/s and θ=30∘, then time of flight will be 1 secBIf u=10√3m/sandθ=60∘, then time of flight will be 3 sec.Cif u=10√3m/sandθ=60∘, then after 2 sec velocity becomes perpendicular to initial velocity.Dif u = 10 m/s and θ=30∘, then velocity never becomes perpendicular to initial velocity during its flight.A particle is moving in a circle with uniform speed v . In moving from a point to another diametrically opposite point
AThe momentum changes by mvBThe momentum changes by 2mvCThe kinetic energy changes by (1/2)mvDThe kinetic energy changes by mv2
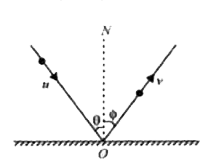
A particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is
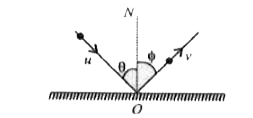
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ to the vertical, and rebounds with a speed v, at an angle ϕ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is
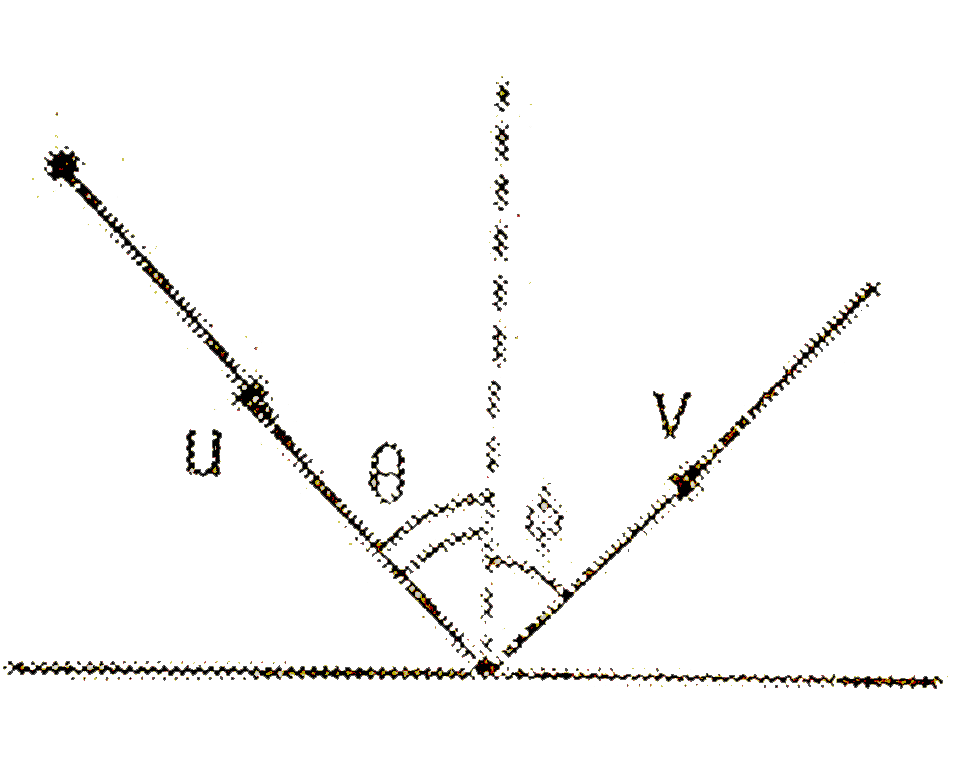
View SolutionA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The angle ϕ is equal to
View SolutionTwo particles A and B are projected simultaneously from a fixed point of the ground. Particle A is projected on a smooth horizontal surface with speed v, while particle B is projected in air with speed v, while particle B is projected in air with speed 2v√3. If particle B hits the particle A, the angle of projection of B with the vertical is
View SolutionA car moves from X to Y with a uniform speed vu and returns to Y with a uniform speed vd. The average speed for this round trip is :
View Solution
