A solid sphere has linear velocity v0=4 m/s and angular velocity ω0=9 rad/s as shown. Ground on which it is moving , is smooth . It collides elastically with a rough wall of coefficient of friction μ . Radius of the sphere is 1m and mass is 2 kg .

If the sphere after colliding with the wall rolls without slipping on opposite direction, then coefdicient of friction μ is
12
23
13
14
The correct Answer is:D
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A solid sphere has linear velocity v0=4m/s and angular velocity ω0=9 rad/s as shown . Ground on which it is moving , is smooth . It collides elastically with a rough wall of coefficient with a rough wall of coefficient of friction μ. Radius of the sphere is 1 m and mass is 2 kg.
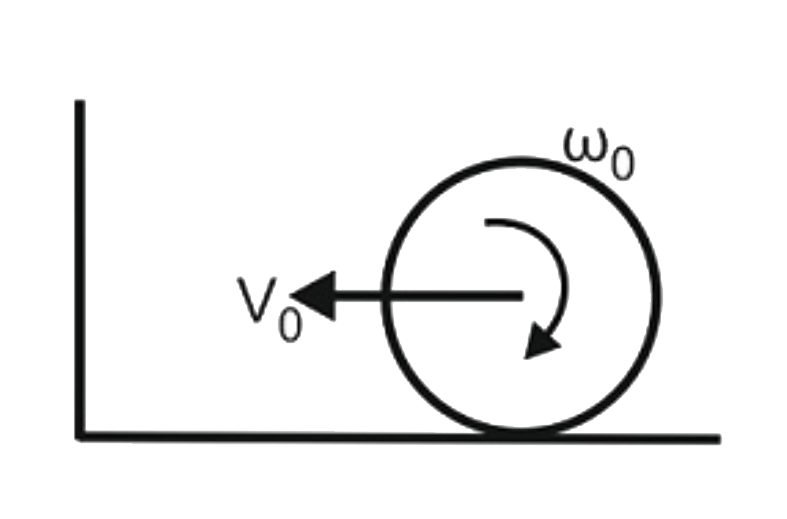
If the sphere after colliding with the wall rolls without slipping in opposite direction, the coefficient of friction μ is
View SolutionA solid sphere has linear velocity v0=4 m/s and angular velocity ω0=9 rad/s as shown. Ground on which it is moving , is smooth . It collides elastically with a rough wall of coefficient of friction μ . Radius of the sphere is 1m and mass is 2 kg .

What is net linear impulse imparted by the wall on the sphere during impact ?
View Solution
Knowledge Check
A solid sphere has linear velocity v0=4 m/s and angular velocity ω0=9 rad/s as shown. Ground on which it is moving , is smooth . It collides elastically with a rough wall of coefficient of friction μ . Radius of the sphere is 1m and mass is 2 kg .

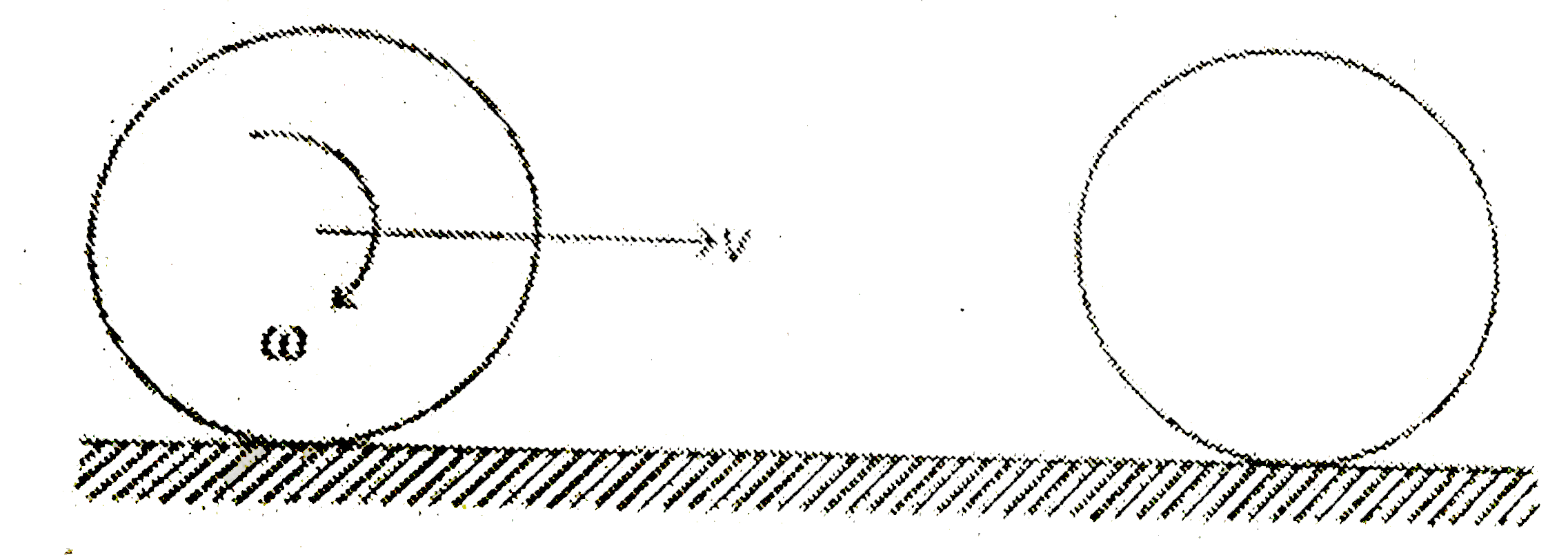
What is net linear impulse imparted by the wall on the sphere during impact ?A√32N−sB4√17N−sC4√5N−sD15√2N−sA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
Linear velocity of first sphere after it again starts rolling without slipping isA25ωRB27ωRC710ωRD75ωRA uniform solid sphere of mass m and radius 'R' is imparted an initial velocity v0 and angular ω0=2v0R and then placed on a rough inclined plane of inclination 'theta' and coefficient of friction μ=2tanθ as shown. The time after which the sphere will start rolling without slipping is
 Av02gsinθBv04gsinθCv06gsinθDv08gsinθ
Av02gsinθBv04gsinθCv06gsinθDv08gsinθ
A solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.

Linear velocity of first sphere after it again starts rolling without slipping is
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. It collides elastically with another identical sphere at rest. There is no friction between the two spheres. Radius of each sphere is R and mass is m.

Linear velocity of first sphere after it again starts rolling without slipping is:
View SolutionA uniform solid sphere of mass m and radius 'R' is imparted an initial velocity v0 and angular ω0=2v0R and then placed on a rough inclined plane of inclination 'theta' and coefficient of friction μ=2tanθ as shown. The time after which the sphere will start rolling without slipping is

View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
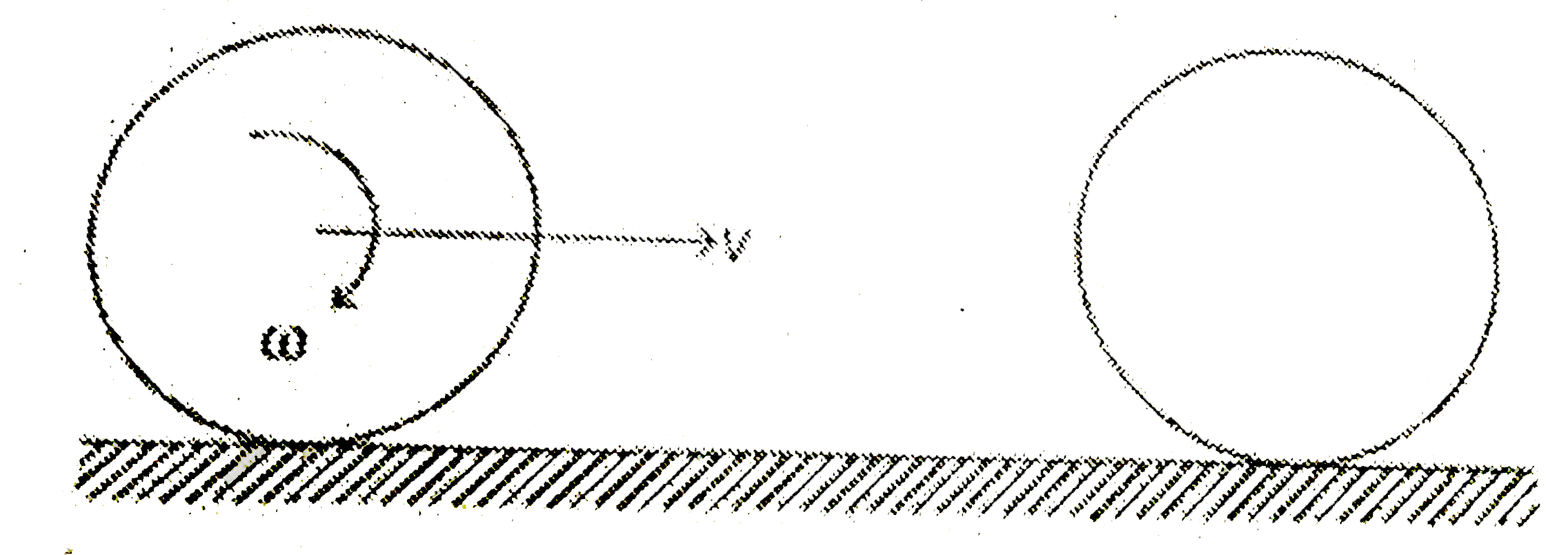
What is the net angular impulse imparted to second sphere by the external forces?
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.

What is the net angular impulse imparted to second sphere by the external forces?
View Solution
