A solid sphere is set into motion on a rough horizontal surfce with a linar speed v in the forward direction and an angular speed v/R in the anticlockwise direction as shown infigure . Find the linear speed of the sphere a. where it stops rotating and b. when slipping finally ceases sand pure rolling starts.

The correct Answer is:A, B, C
a. If we take moment at A then external torque will be zero.
Thereforethe∈itialanga––rmomentum=theanga––rmomentumafterrotations⊤(i.e.onlyl∈earvelocity∃).<br>MVxxR-(2/5)Ixxw=MV_0xxR<br>rarr MVR-2/5xxMR^2V/R=MV_0R<br>rarr V_0=(3V)/5<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C10_E01_148_S01.pngwh=80%mx-autosty≤=background:white;><br>b.Aga∈aftersometimepureroll∈g⋆ts.<br>Therefore
→MxV0×R=(25)MR2×(VR)+Mv'R
→m×3V7
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions

A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.
View SolutionA rigid bodyI=CMR2 is set into a motion on a rough horizontal surface with a linear speed v0 in the forward direction at time t = 0 as shown in figure. After what time slipping finally stop and pure rolling starts. Find the linear speed of the body after it starts pure rolling on the surface.
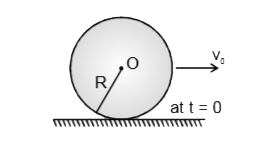
View Solution
Knowledge Check
A solid sphere is set into motion on a rough horizontal surface with a linear velocity v in the forward direction and an angular velocity v/R in the anticlockwise direction as shown in the figure. Find the linear speed of the sphere, when it stops rotating.
 Av5Bv7C3v5D3v7
Av5Bv7C3v5D3v7A symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
Av/RBContinuously increasingCDependent on mass MDIndependent of radius (R)A solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
Ait will move with a speed v initiallBits motion will be rolling with slipping initially and its rotational motion will stop momentarily at some instant.Cits motion will be rolling without slipping only after some timeDall of the above.
A solid sphere of radius R is set into motion on a rough horizontal surface with a linear speed v0 in forward direction and an angular with a linear speed v0 in forward direction and an angular velocity ω0=v0/2R in counter clockwise direction as shown in figure. If coefficient of friction μ then find
a. the time after which sphere starts pure rolling,
b. the linear speed of sphere when it starts rolling and
c. the work down by friction over a long time.
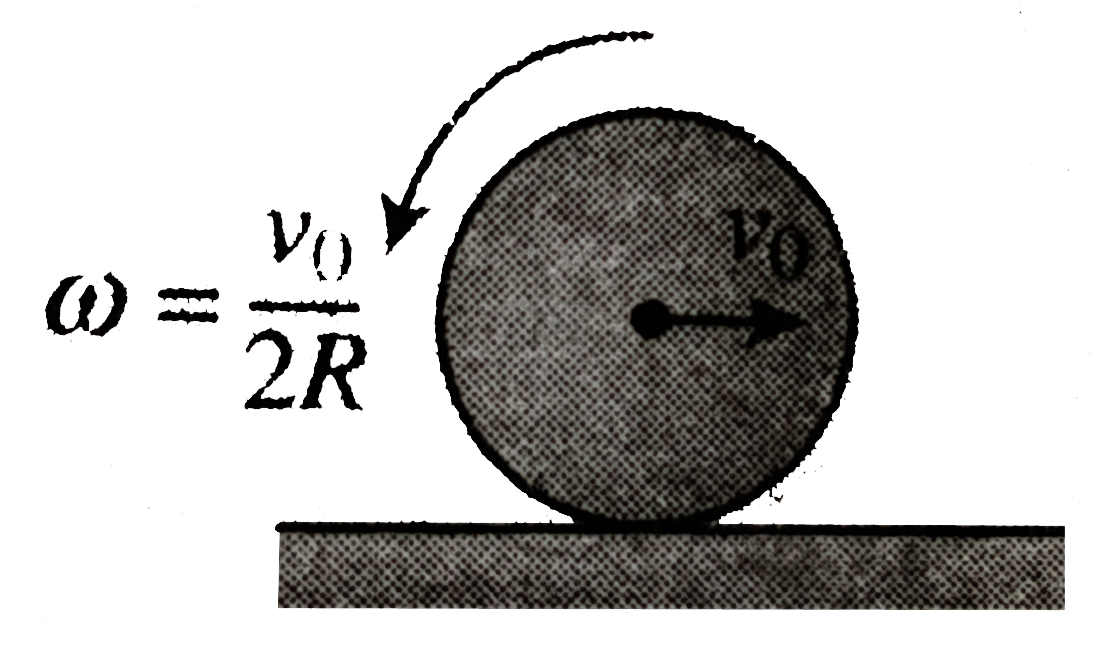
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionA solid sphere rolling on a rough horizontal surface with a linear speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View Solution(i) A solid sphere of radius R is released on a rough horizontal surface with its top point having thrice the velocity of its bottom point A (VA=V0) as shown in figure. Calculate the linear velocity of the centre of the sphere when it starts pure rolling.
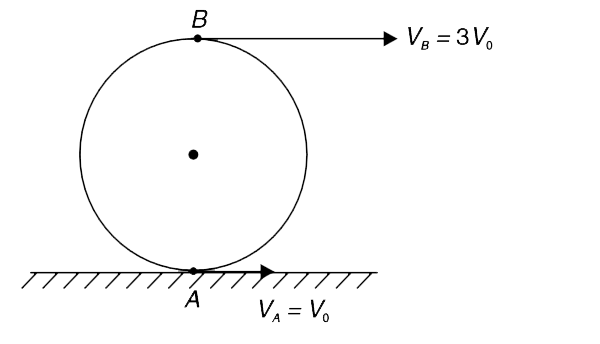
(ii) Solid sphere of radius R is placed on a rough horizontal surface with its centre having velocity V0 towards right and its angular velocity being ω0 (in anticlockwise sense). Find the required relationship between V0 and ω0 so that -
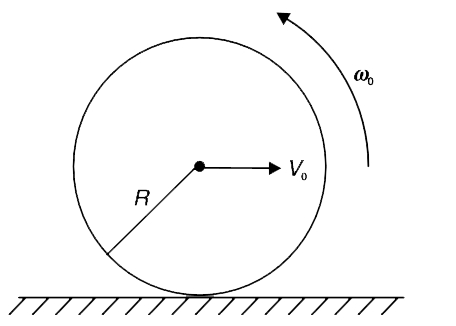
(a) the slipping ceases before the sphere loses all its linear momentum.
(b) the sphere comes to a permanent rest after some time.
(c) the velocity of centre becomes zero before the spinning ceases.
View SolutionA solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
View Solution
