A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
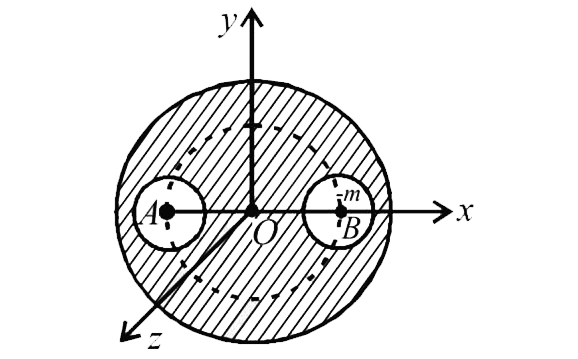
the gravitational force due to this object at the origin is zero
the gravitational force at point B(2,0,0) is zero
the gravitational potential is the same at all points of circle y2+z2q=36
Both (a) and (c)
The correct Answer is:A, C, D
The gravitational field intensity at point O is zero (as the cavities are symmetrical with respect to O).
Now the force acting on a test mass m0 placed at O is given by
F=m0E=m0×0=0 
Now y2+z2=36 represents the equation of a circle with centre (0,0,0) and radius 6 units. The plane of the circle is perpendicular to the axis. Since the spherical mass distribution behaves as if the whole mass is at its centre (for a point outside the sphere) and since all the points on the circle are equidistant from the centre of the sphere, the circle is a gravitational equipotential.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - AR_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - SCQ_TYPE12videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
Similar Questions
A nonconducting sphere of radius R=5cm has its center at the origin O of the coordinate system as shown in (Fig. 3.112). It has two spherical cavities of radius r=1cm, whose centers are at 0,3cm and 0,−3cm, respectively, and solid material of the sphere has uniform positive charge density ρ=1/πμCm−3. Calculate the electric potential at point P(4cm,0).
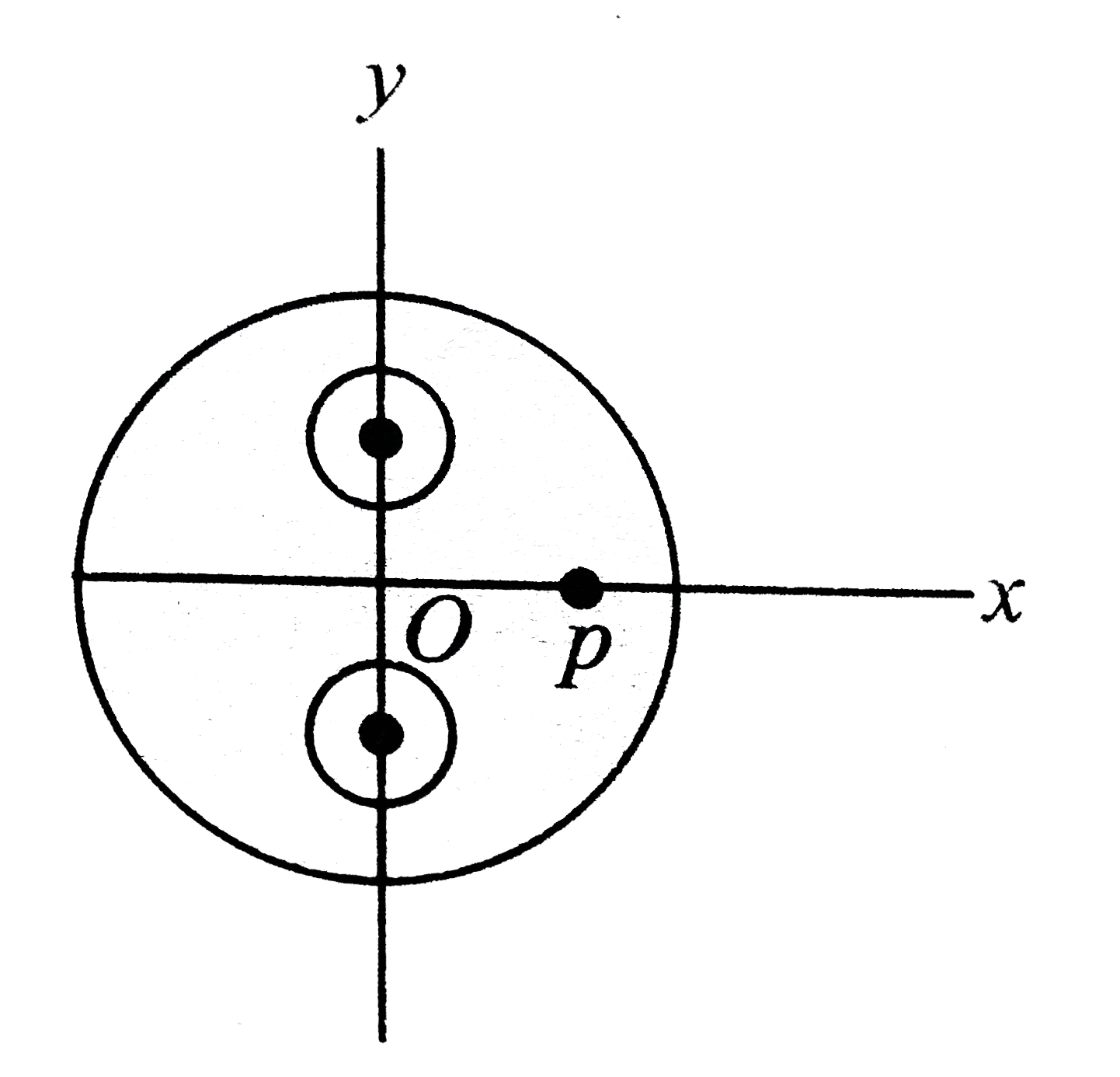.View SolutionA solid sphere having uniform charge density ρ and radius R is shown in figure. A spherical cavity ofradius R2 is made in it. What is the potential at point O?
View Solution
Knowledge Check
- Question 1 - Select One
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
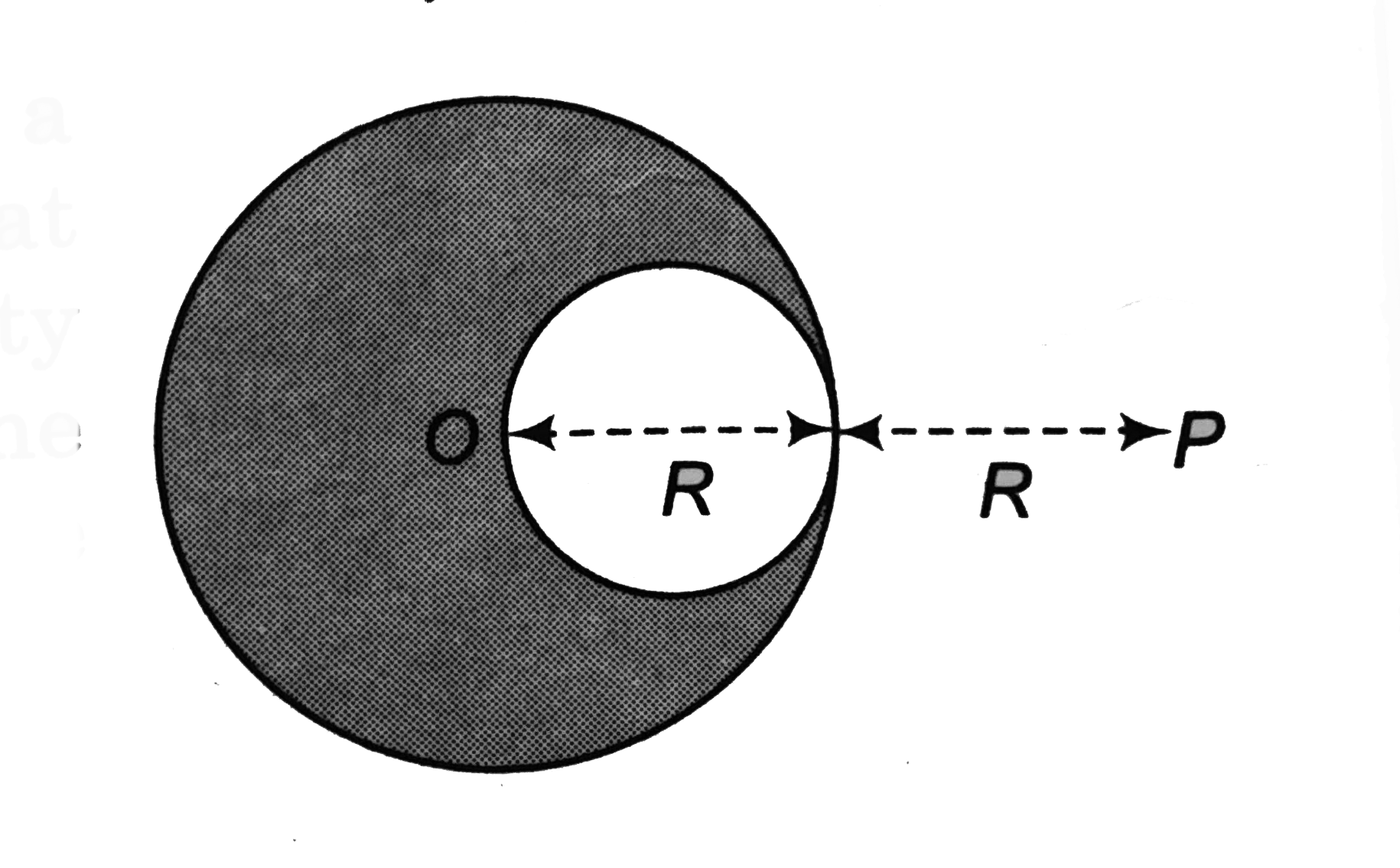A1/2B7/9C3D7
Consider a solid sphere of density ρ and radius 4R. Centre of the sphere is at origin. Two spherical cavities centred at (2R,0) and (−2R,0) are created in sphere. Radii of both cavities is R. In left cavity material of density 2ρ is filled while second cavity is kept empty. What is gravitational field at origin.
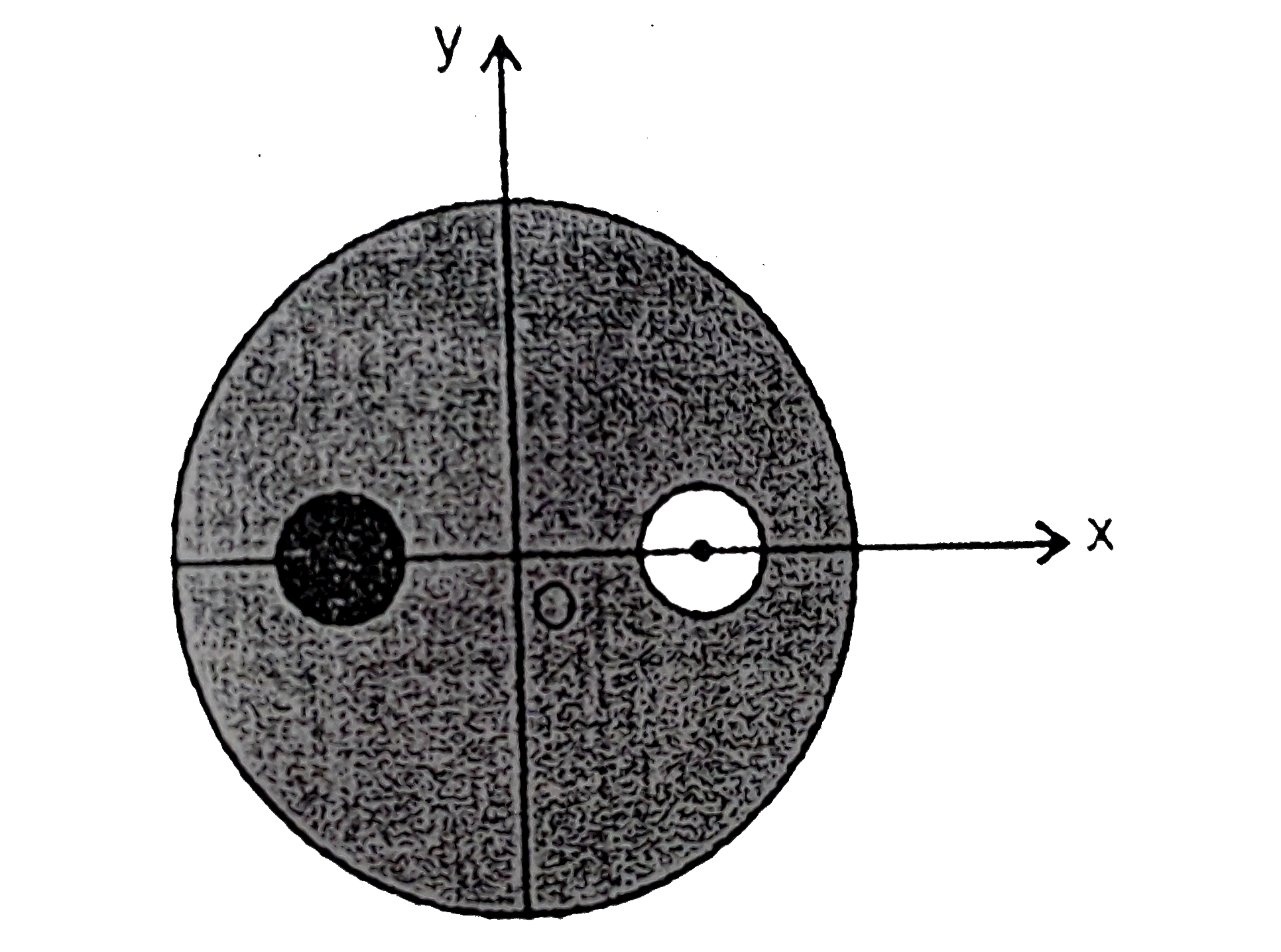
View SolutionA solid sphere of uniform density and radius R applies a gravitational force attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shows in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
View SolutionA solid sphere of mass M and radius R is in pure rolling as shown in figure. The angular momentum of the sphere about the origin is (linear velocity of centre of mass is v0, in positive x-direction)
View SolutionThe gravitational force acting on a particle, due to a solid sphere of uniform density and radius R, at a distance of 3R from the centre of the sphere is F1. A spherical hole of radius (R/2) is now made in the sphere as shown in diagram. The sphere with hole now exerts a force F2 on the same particle. ratio of F1 to F2 is
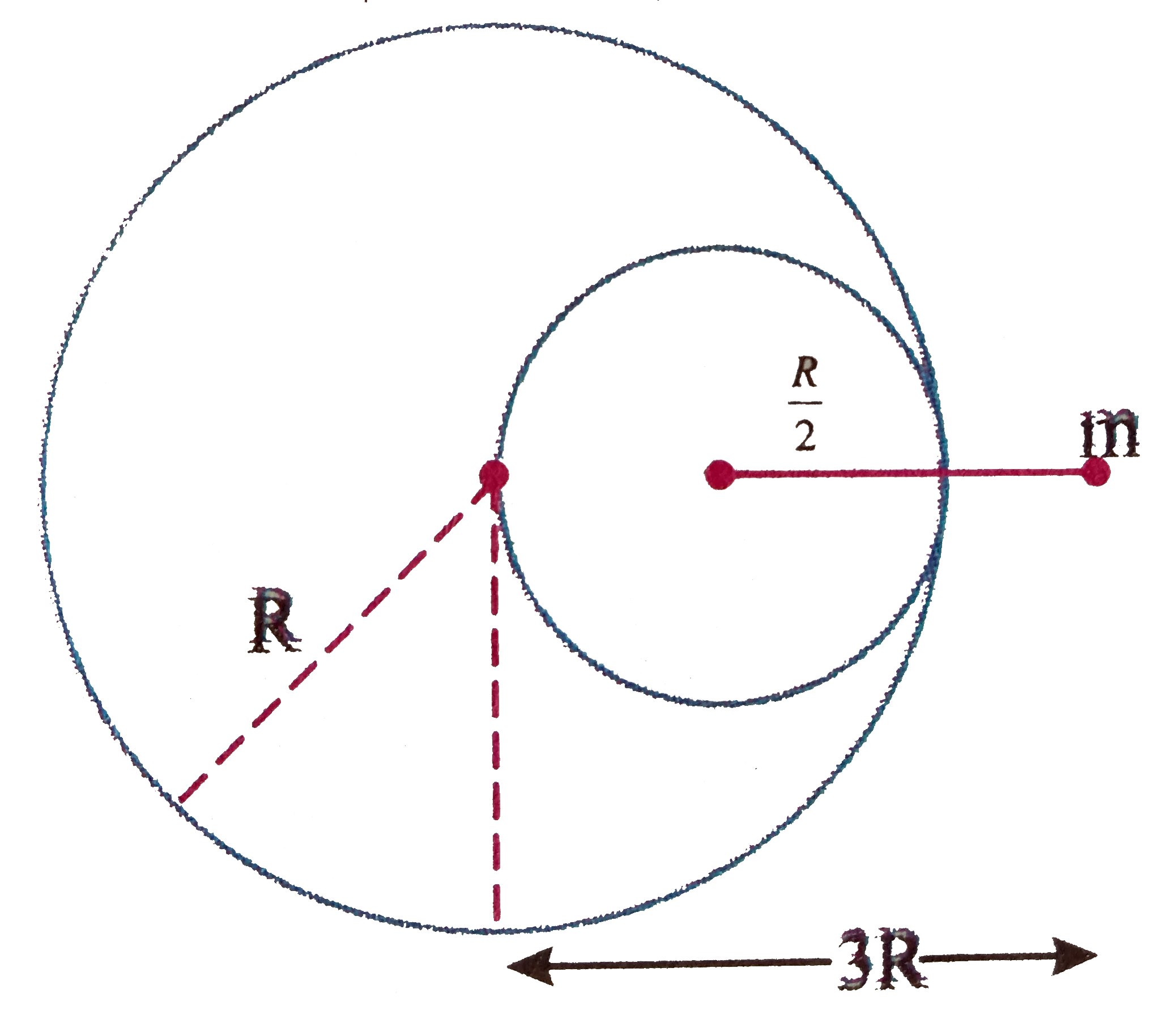
View SolutionA circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is
View SolutionCalculate the void space in closest packing of n spheres of radius 1 unit, n spheres of radiys 0.414 units, and 2n spheres of radius 0.225 units.
View Solution