A spherical condenser has innder and outer spheres of radii a and b respectively. The space between the two is filled with air. The difference between the capacities of two condensers formed when outer sphere is earthed and when inner sphere is earthed will be
zero
4πε0a
4πε0b
4πε0a(bb−a)
The correct Answer is:C
To solve the problem, we need to calculate the capacitance of a spherical capacitor in two different scenarios: when the outer sphere is earthed and when the inner sphere is earthed. We will then find the difference between these two capacitances.
1. Understanding the Spherical Capacitor:
- A spherical capacitor consists of two concentric spherical conductors: an inner sphere of radius a and an outer sphere of radius b.
- The space between the two spheres is filled with air.
2. Capacitance when Outer Sphere is Earthed (C1):
- When the outer sphere is earthed, it is at zero potential.
- The potential V at the inner sphere (radius a) due to a charge Q on it is given by:
V=14πϵ0⋅Qa
- The potential at the outer sphere (radius b) is zero because it is earthed.
- The capacitance C1 is given by:
C1=QV=QQ4πϵ0a=4πϵ0abb−a
3. Capacitance when Inner Sphere is Earthed (C2):
- When the inner sphere is earthed, its potential is zero.
- The potential V at the outer sphere (radius b) due to a charge Q on the outer sphere is:
V=14πϵ0⋅(Qb−Qa)
- Setting the potential of the inner sphere to zero gives:
Qb−Qa=0⟹Q=Qb⋅a
- The capacitance C2 is given by:
C2=QV=QQ4πϵ0b−Q4πϵ0a=4πϵ0aba−b
4. Finding the Difference in Capacitance:
- We need to find the difference C2−C1:
C2−C1=4πϵ0(aba−b−abb−a)
- Simplifying this expression:
C2−C1=4πϵ0(ab(b−a)−ab(a−b)(a−b)(b−a))
- This simplifies to:
C2−C1=4πϵ0a
5. Final Result:
- The difference between the capacitances when the outer sphere is earthed and when the inner sphere is earthed is:
4πϵ0a
- A spherical capacitor consists of two concentric spherical conductors: an inner sphere of radius a and an outer sphere of radius b.
- The space between the two spheres is filled with air.
- When the outer sphere is earthed, it is at zero potential.
- The potential V at the inner sphere (radius a) due to a charge Q on it is given by:
V=14πϵ0⋅Qa
- The potential at the outer sphere (radius b) is zero because it is earthed.
- The capacitance C1 is given by:
C1=QV=QQ4πϵ0a=4πϵ0abb−a
- When the inner sphere is earthed, its potential is zero.
- The potential V at the outer sphere (radius b) due to a charge Q on the outer sphere is:
V=14πϵ0⋅(Qb−Qa)
- Setting the potential of the inner sphere to zero gives:
Qb−Qa=0⟹Q=Qb⋅a
- The capacitance C2 is given by:
C2=QV=QQ4πϵ0b−Q4πϵ0a=4πϵ0aba−b
- We need to find the difference C2−C1:
C2−C1=4πϵ0(aba−b−abb−a)
- Simplifying this expression:
C2−C1=4πϵ0(ab(b−a)−ab(a−b)(a−b)(b−a))
- This simplifies to:
C2−C1=4πϵ0a
- The difference between the capacitances when the outer sphere is earthed and when the inner sphere is earthed is:
4πϵ0a
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
The radii of the inner and outer circumferences of a circular-running-track are 63 m and 70 m respectively. Find :
(i) the area of the track
(ii) the difference between the lengths of the two circumferences of the track
View SolutionA hollow spherical body of inner and outer radii 6 cm, and 8 cm respectively floats half submerged in water. Find the density of the material of the sphere.
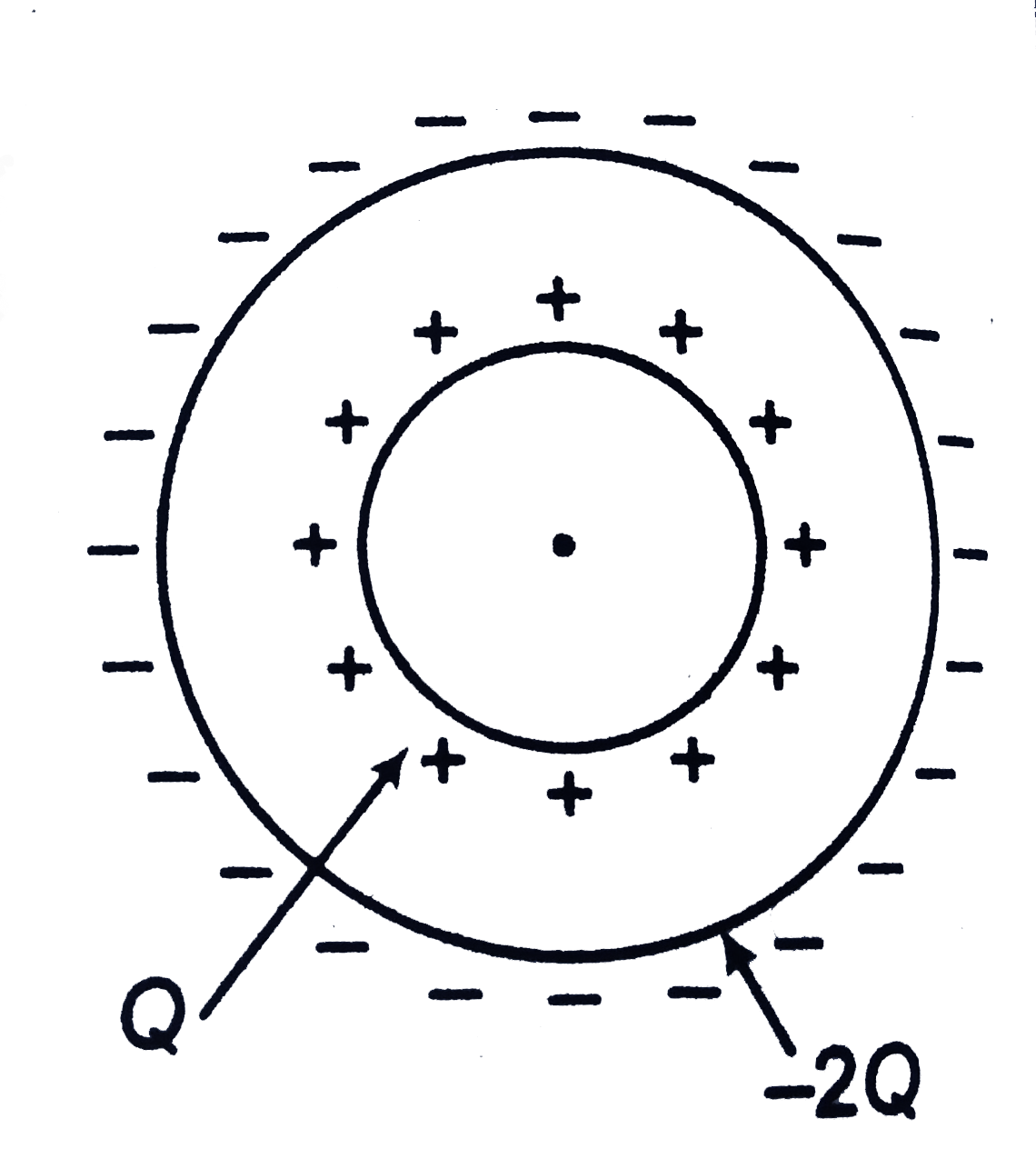
View SolutionTwo concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
View SolutionTwo homogeneous spheres A and B of masses m and 2m having radii 2a and a respectively are placed in touch . The distance of the centre of mass from the first sphere is
View SolutionTwo hollow concentric non-conducting spheres of radius the a and b(a>b) contain charges Qa and Qb respectively. Prove that potential difference between the two spheres is independent of charge on outer sphere. If outer sphere is given an extra charge, is there any change in potential difference ?
View SolutionA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
View SolutionA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
View SolutionTwo identical spheres of radii 10 cm each are placed in between two rigid walls (vertical) as shown. The spacing between the walls is 36 cm. Then find the force of contact between the spheres, if the weight of each sphere is 'W'.
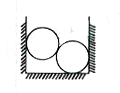
View SolutionA spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5μC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor. (b) What is the potential of the inner sphere ?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm.Explain why the later is much smaller ?
View SolutionA hollow metallic sphere of radius 20cm surrounds a concentric metallic sphere of radius 5cm. The space between the two sphere is filled with a nonmetallic material. The inner and outer sphere are maintained at 50∘C and 10∘C respectively and it is found that 100J of heat passes from the inner sphere to the outer sphere per second. Find the thermal conductivity of the material between the sphere.
View Solution
