A square frame of side l carries a current produces a field B at its centre. The same current is passed through a circular loop having same perimeter as the square. The field at its centre is B', the ratio of B/B' is
8π2
8√2π2
16π2
16√2π2
The correct Answer is:B
To solve the problem, we need to find the ratio of the magnetic field B produced by a square frame carrying a current at its center to the magnetic field B′ produced by a circular loop with the same perimeter carrying the same current.
1. Determine the Magnetic Field B at the Center of the Square Frame:
- The magnetic field at the center of a square loop of side length l carrying a current I is given by the formula:
B=μ0I4πl⋅√2
- Since there are 4 sides, the total magnetic field becomes:
B=4μ0I4πl⋅√2=μ0I√2πl
2. Determine the Radius r of the Circular Loop:
- The perimeter of the square is 4l.
- The perimeter of the circular loop is 2πr.
- Setting these equal gives:
4l=2πr⟹r=4l2π=2lπ
3. Determine the Magnetic Field B′ at the Center of the Circular Loop:
- The magnetic field at the center of a circular loop of radius r carrying a current I is given by:
B′=μ0I2r
- Substituting the value of r:
B′=μ0I2⋅2lπ=μ0Iπ4l
4. Calculate the Ratio BB′:
- Now, we can find the ratio of the magnetic fields:
BB′=μ0I√2πlμ0Iπ4l
- Simplifying this expression gives:
BB′=√2π4=4√2π
5. Final Result:
- Thus, the ratio BB′ is:
BB′=4√2π
- The magnetic field at the center of a square loop of side length l carrying a current I is given by the formula:
B=μ0I4πl⋅√2
- Since there are 4 sides, the total magnetic field becomes:
B=4μ0I4πl⋅√2=μ0I√2πl
- The perimeter of the square is 4l.
- The perimeter of the circular loop is 2πr.
- Setting these equal gives:
4l=2πr⟹r=4l2π=2lπ
- The magnetic field at the center of a circular loop of radius r carrying a current I is given by:
B′=μ0I2r
- Substituting the value of r:
B′=μ0I2⋅2lπ=μ0Iπ4l
- Now, we can find the ratio of the magnetic fields:
BB′=μ0I√2πlμ0Iπ4l
- Simplifying this expression gives:
BB′=√2π4=4√2π
- Thus, the ratio BB′ is:
BB′=4√2π
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Papper 350videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 150videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 350videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT Exemplar11videos
RAY OPTICS AND OPTICAL INSTRUMENTS
Similar Questions
Knowledge Check
- Question 1 - Select One
Current flows through uniform square frames as shown. In which case is the magnetic field at the centre of the frame not zero ?
A B
B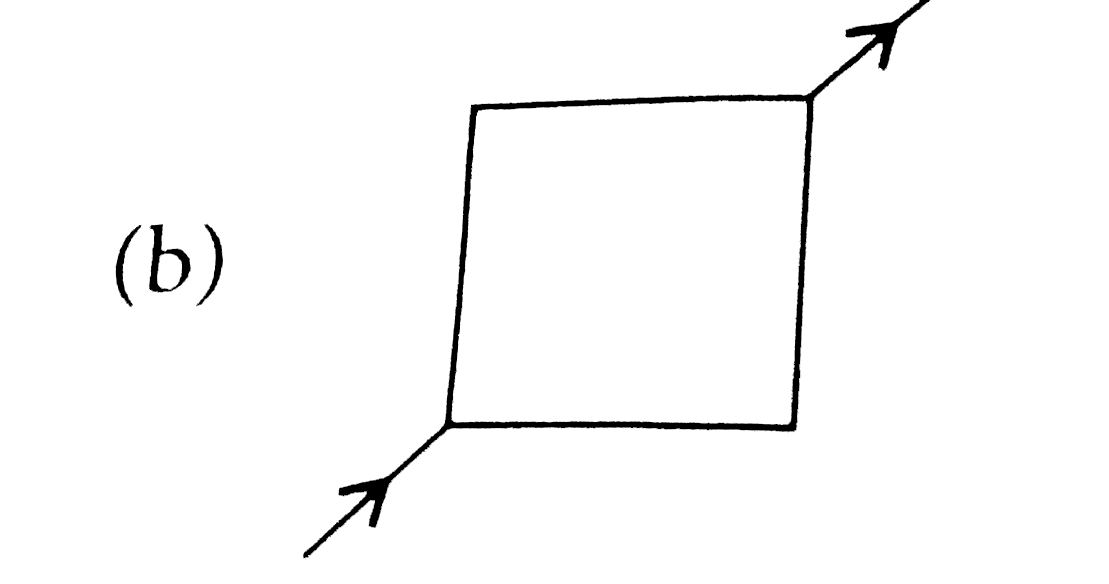 C
C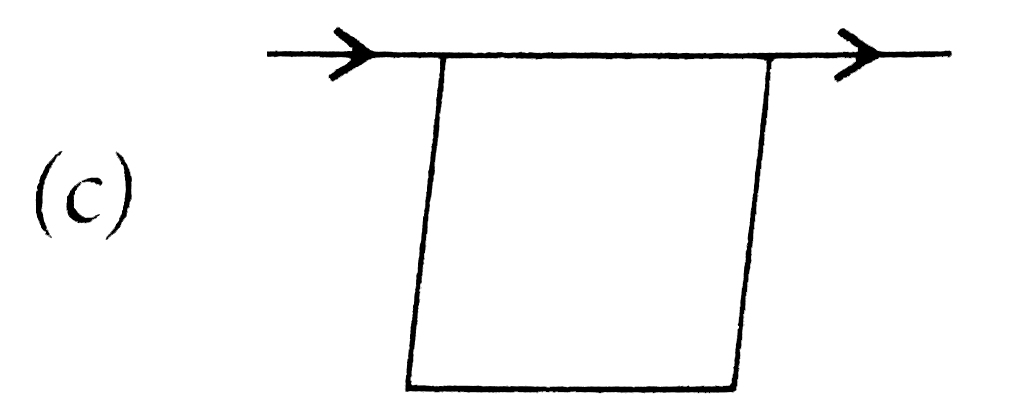 D
D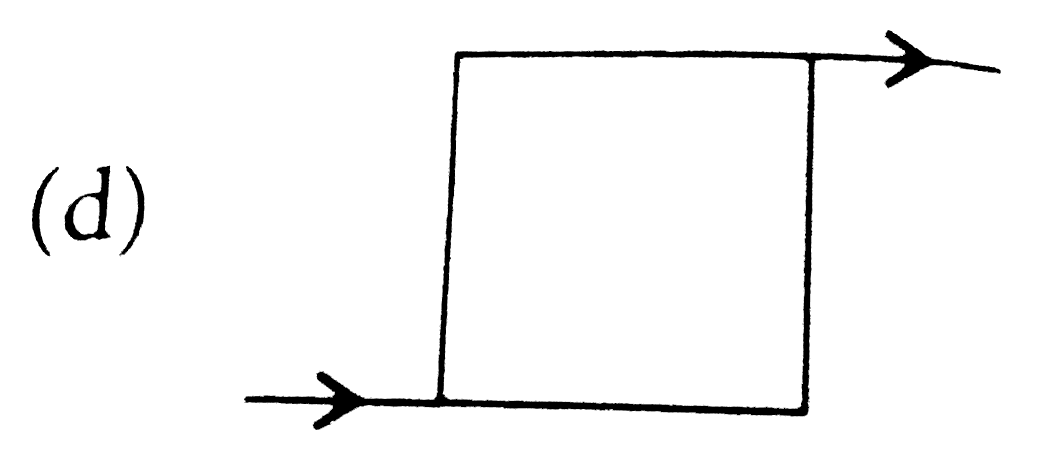
A square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)
View SolutionA circular coil carrying a certain, current produces a magnetic field B0 at its center. The coil is now rewound so as to have 3 turns and the same currents is passed through it. The new magnetic field at the center is
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionA circular coil of radius R carries a current i. The magnetic field at its centre is B. The distance from the centre on the axis of the coil where the magnetic field will be B/8 is
View SolutionA steady current is flowing in a circular coil of radius R, made up of a thin conducting wire. The magnetic field at the centre of the loop is BL. Now, a circular loop of radius R/n is made from the same wire without changing its length, by unfounding and refolding the loop, and the same current is passed through it. If new magnetic field at the centre of the coil is BC, then the ratio BL/BC is
View SolutionA steady current is flowing in a circular coil of radius R, made up of a thin conducting wire. The magnetic field at the centre of the loop is BL. Now, a circular loop of radius R/n is made from the same wire without changing its length, by unfounding and refolding the loop, and the same current is passed through it. If new magnetic field at the centre of the coil is BC, then the ratio BL/BC is
View SolutionA long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the centre of the loop is B. it is then bent into a circular coil of n turns. The magnetic field at the centre of this coil of n turns will be
View Solution

