A square loop of edge b having M turns is rotated with a uniform angular velocity $ω$ about one of its diagonals which is kept fixed in a horizontal position. A uniform magnetic field $B_{0}$ exists in the vertical direction.

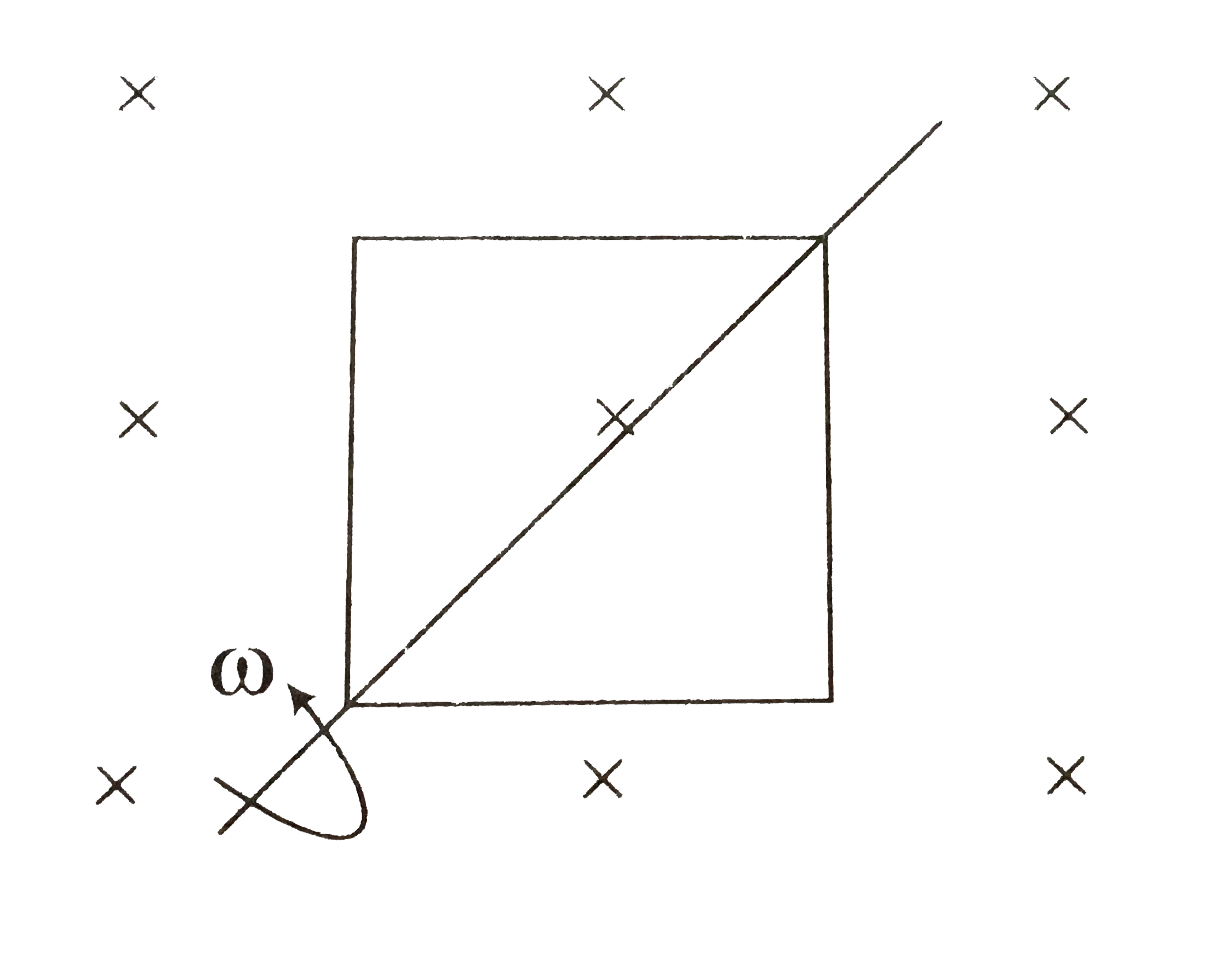
Find (i) the emf induced in the coil as a function of time t.
(ii) the maximum emf induced.
(iii) the average emf induced in the loop over a long period.
(iv) if resistance of loop is R, amount of charge flown in time t = 0 to t = 2T.
(v) heat produced in time t = 0 to t = 2T.

Video Solution

Text Solution

Verified by Experts

Initially, plane of loop is $⊥^{a r}$ to the field. Let at any time, normal to loop makes an angle $θ$ with magnetic field $θ = ω t$ .
The flux passing through loop,
$ϕ_{B} = M B_{0} S \cos θ = M B_{0} b^{2} \cos ω t$
$\Rightarrow e = - \frac{d ϕ_{B}}{d t} = M B_{0} b^{2} ω \sin ω t = e_{0} \sin ω t,$
where, $e_{0} = M B_{0} b^{2} ω$
(ii) For emf to be maximum, then sin $ω t$ should be equal to 1.
$\Rightarrow e_{max} = e_{0}$
(iii) Long period means one time period, i.e., $0 \to T$
We know that average emf is given as
$\bar{e} = \frac{\int_{0}^{T} e d t}{\int_{0}^{T} d t} = \frac{1}{T} . e_{0} \int_{0}^{T} \sin ω t d t = 0 (∵ \int_{0}^{T} \sin ω t d t = 0)$
(iv) Using the relation, induced current,
$i = \frac{e}{R} = \frac{e_{0}}{R} \sin ω t = i_{0} \sin ω t$
where, $i_{0} = \frac{e_{0}}{R}$ .
We know q = idt
So, for time $O \to 2 T$ ,
$q = \int_{0}^{2 T} idt = i_{0} \int_{0}^{2 T} \sin ω t d t = 0$
(v) Heat (H) generated in a loop during time $0 \to 2 T$ , is given as
$H = \int_{0}^{2 T} \frac{e^{2}}{R} d t = \frac{e_{0}^{2}}{0} \int_{0}^{2 T} \sin^{2} ω t d t$
$= \frac{e_{0}^{2}}{R} .2 . \frac{T}{2} = \frac{e_{0}^{2}}{R} . \frac{2 π}{ω} = \frac{2 π e_{0}^{2}}{ω R} (∵ T = \frac{2 π}{ω})$

|

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

DC PANDEY ENGLISH-ELECTROMAGNETIC INDUCTION-Example

Home
Ask Doubt
Profile