A square loop of side .a. lying in a perpendicular magnetic field to its plane is changed to a circle. If change occurs in .t. seconds in magnetic field B tesla, the induced emf is
4πBa2t
Ba2t
Ba2t[4π−1]
zero
To solve the problem step by step, we will follow the concepts of electromagnetic induction, specifically Faraday's law of electromagnetic induction.
1. Identify the Initial and Final Shapes:
- The initial shape is a square loop with side length a.
- The final shape is a circular loop.
2. Calculate the Area of the Square Loop:
- The area Asquare of the square loop is given by:
Asquare=a2
3. Relate the Perimeter of the Square to the Circumference of the Circle:
- The perimeter of the square loop is 4a.
- The circumference of the circular loop is 2πr.
- Setting these equal gives:
4a=2πr
- From this, we can solve for r:
r=4a2π=2aπ
4. Calculate the Area of the Circular Loop:
- The area Acircle of the circular loop is given by:
Acircle=πr2
- Substituting r:
Acircle=π(2aπ)2=π⋅4a2π2=4a2π
5. Determine the Change in Area:
- The change in area ΔA is:
ΔA=Acircle−Asquare=4a2π−a2
- Simplifying this gives:
ΔA=a2(4π−1)
6. Calculate the Induced EMF:
- According to Faraday's law, the induced EMF E is given by:
E=−dΦdt
- The magnetic flux Φ is given by Φ=B⋅A, where B is the magnetic field.
- Thus, the rate of change of magnetic flux is:
dΦdt=B⋅dAdt
- Since dA=ΔA and dt=t:
E=−B⋅ΔAt
- Substituting ΔA:
E=−B⋅a2(4π−1)t
7. Final Expression for Induced EMF:
- The induced EMF can be expressed as:
E=Ba2t(4π−1)
- The initial shape is a square loop with side length a.
- The final shape is a circular loop.
- The area Asquare of the square loop is given by:
Asquare=a2
- The perimeter of the square loop is 4a.
- The circumference of the circular loop is 2πr.
- Setting these equal gives:
4a=2πr
- From this, we can solve for r:
r=4a2π=2aπ
- The area Acircle of the circular loop is given by:
Acircle=πr2
- Substituting r:
Acircle=π(2aπ)2=π⋅4a2π2=4a2π
- The change in area ΔA is:
ΔA=Acircle−Asquare=4a2π−a2
- Simplifying this gives:
ΔA=a2(4π−1)
- According to Faraday's law, the induced EMF E is given by:
E=−dΦdt
- The magnetic flux Φ is given by Φ=B⋅A, where B is the magnetic field.
- Thus, the rate of change of magnetic flux is:
dΦdt=B⋅dAdt
- Since dA=ΔA and dt=t:
E=−B⋅ΔAt
- Substituting ΔA:
E=−B⋅a2(4π−1)t
- The induced EMF can be expressed as:
E=Ba2t(4π−1)
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE - I (MAGNETIC FLUX, FARADAY.S LAW, LENZ.S LAW, AC GENERATOR)26videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE - I (SELF AND MUTUAL INDUCTION)16videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-II32videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
Similar Questions
A square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA square loop of side 1 m is placed in a perpendicular magnetic field. Half of the area of the loop lies inside the magnetic field . A battery of emf 10 V and negligible intermal resistance is connected in the loop . The magnetic field changes with time according to the relation B= (0.01 -2t) tesla . The resultant emf of the circuit is
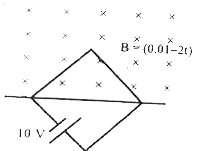 View Solution
View SolutionA wire of length l in the form of a square loop lies in a plane normal to a magnetic field B0. If this wire is converted into a circular loop in time, then find the average induced emf.
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View SolutionA square loop of side 5 cm enters a magnetic field with 1cms−1. The front edge enters the magnetic emf?
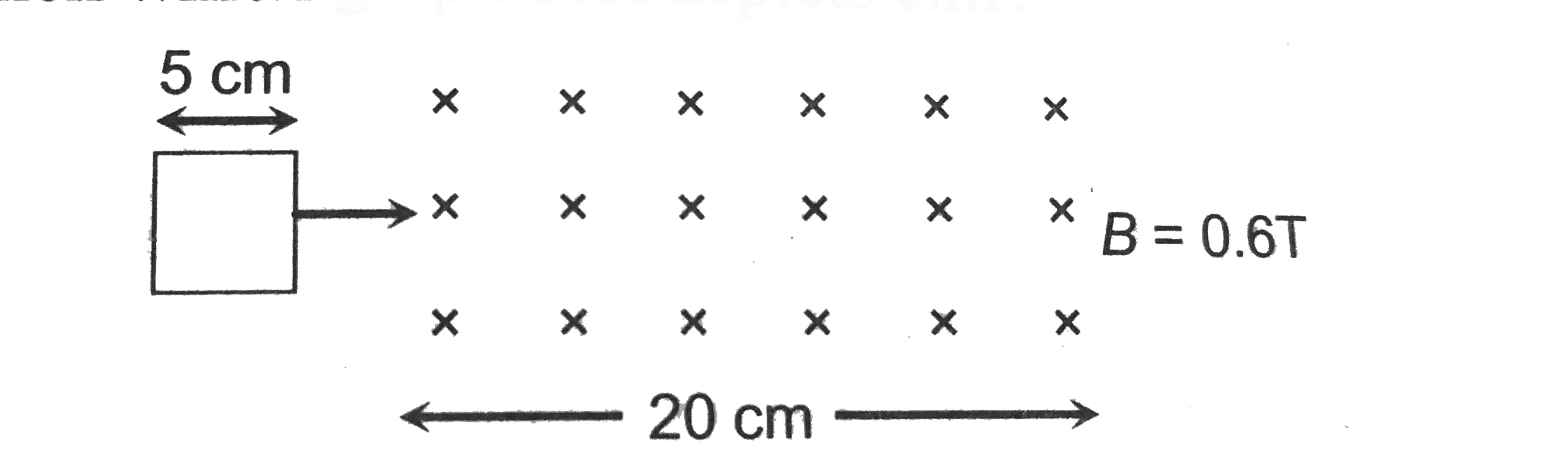 View Solution
View SolutionA square coil AECD of side 0.1m is placed in a magnetic field B=2t2. Here, t is in seconds and B is Tesla. The magnetic field is into the paper. At time t=2s, induced field in DC in
 View Solution
View SolutionA circular loop of radius 1m is placed in a varying magnetic field given as B=6t Tesla, where t is time in sec.
(a)Find the emf induced in the coil if the plane of the coil is perpendicular to the magnetic field.
(b) Find the electric field in the tangential directin, induced due to the changing magnetic field.
(c)Find the current in the loop if its resistance is 1Ω/m.View SolutionA square loop of side 10 cm with its side parallel to X, and y axis is kept in a uniform magnetic field pointing towards positive z-direction. If magnetic field changes at the rate of 0.1 T/s, then induced emf is
View SolutionElectric field induced by changing magnetic fields are
View SolutionA square loop of side b is rotated in a constant magnetic field B at angular frequency ω as shown in the figure. What is the emf induced in it?
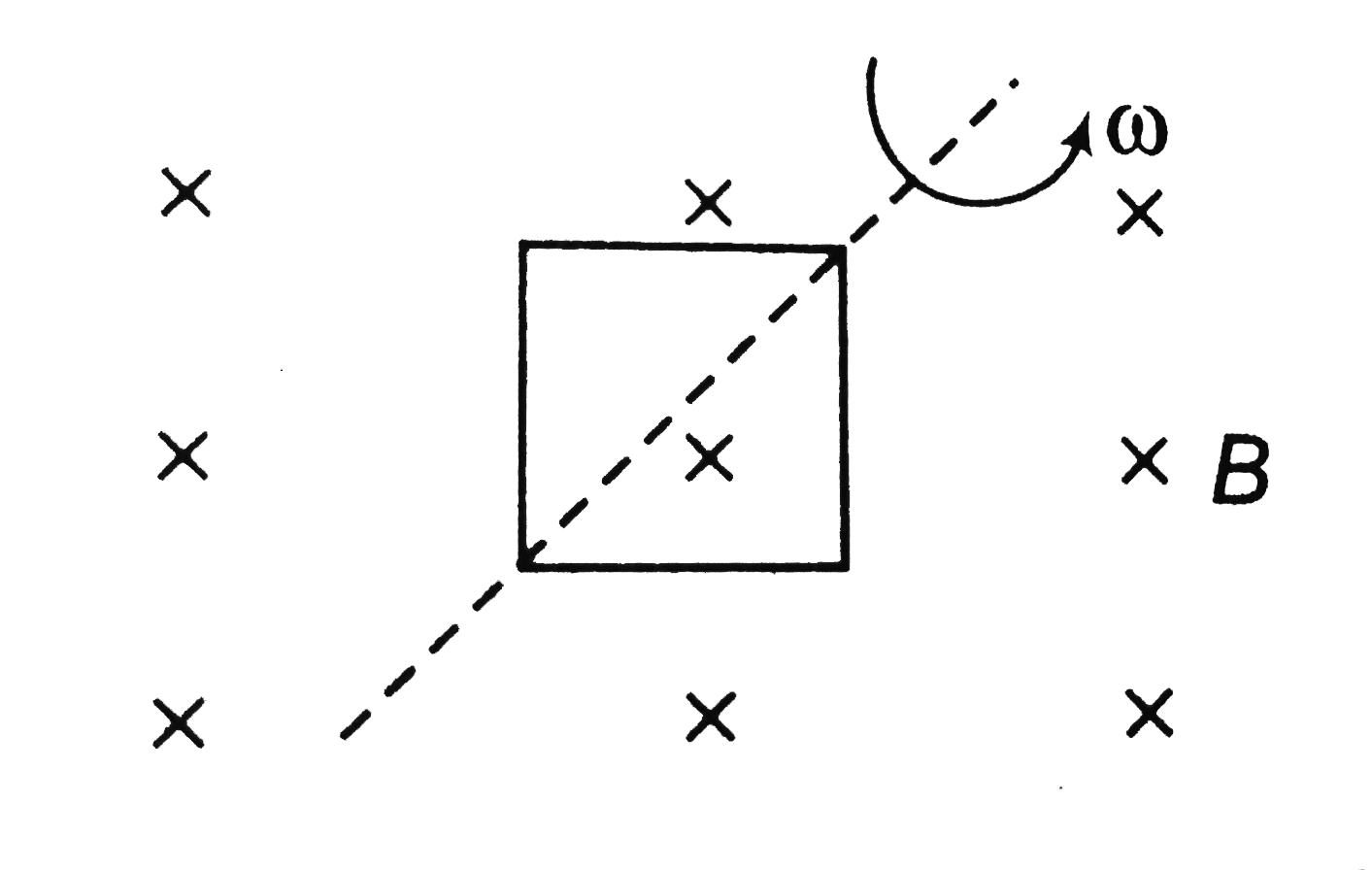 View Solution
View Solution

