A square loop of side 10 cm with its side parallel to X, and y axis is kept in a uniform magnetic field pointing towards positive z-direction. If magnetic field changes at the rate of 0.1 T/s, then induced emf is
1.0 mV
0.5 mV
1.5 mV
03 mV
To solve the problem of finding the induced emf in a square loop placed in a changing magnetic field, we can follow these steps:
Step 1: Understand the given parameters
- The side of the square loop (a) = 10 cm = 0.1 m
- The rate of change of the magnetic field (dB/dt) = 0.1 T/s
- The area (A) of the square loop can be calculated as A=a2.
Step 2: Calculate the area of the square loop
A=(0.1m)2=0.01m2
Step 3: Use Faraday's Law of Electromagnetic Induction
According to Faraday's law, the induced emf (ε) in a loop is given by:
ϵ=−dΦdt
Where Φ (magnetic flux) is given by:
Φ=B⋅A
Since the magnetic field is changing, we can express the change in flux as:
dΦdt=A⋅dBdt
Step 4: Substitute the values into the equation
Now substituting the values we have:
ϵ=−A⋅dBdt
ϵ=−0.01m2⋅0.1T/s
Step 5: Calculate the induced emf
ϵ=−0.001V=−1mV
Since we are interested in the magnitude of the induced emf, we can ignore the negative sign:
ϵ=1mV
Final Answer
The induced emf is 1 millivolt (mV).
---
- The side of the square loop (a) = 10 cm = 0.1 m
- The rate of change of the magnetic field (dB/dt) = 0.1 T/s
- The area (A) of the square loop can be calculated as A=a2.
A=(0.1m)2=0.01m2
According to Faraday's law, the induced emf (ε) in a loop is given by:
ϵ=−dΦdt
Where Φ (magnetic flux) is given by:
Φ=B⋅A
Since the magnetic field is changing, we can express the change in flux as:
dΦdt=A⋅dBdt
Now substituting the values we have:
ϵ=−A⋅dBdt
ϵ=−0.01m2⋅0.1T/s
ϵ=−0.001V=−1mV
Since we are interested in the magnitude of the induced emf, we can ignore the negative sign:
ϵ=1mV
The induced emf is 1 millivolt (mV).
Topper's Solved these Questions
Similar Questions
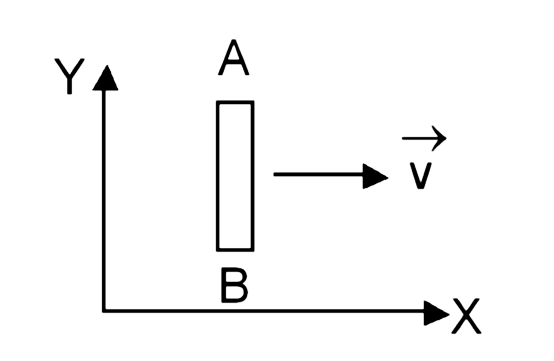
A conductor rod AB moves parallel to X-axis in a uniform magnetic field, pointing in the positive Z-direction. The end A of the rod gets-
View SolutionA square loop of side 12 cm with its sides parallel to X and Y axes is moved with a velocity of 8 cm s−1 in the positive x-direction in an environment containing a magnetic field in the positive z-direction. The field is neither uniform in space nor constant in time. It has a gradient of 10−3Tcm−1 along the negative x-direction (that is it increases by 10−3Tcm−1as one moves in the negative x-direction), and it is decreasing in time at the rate of 10−3Ts−1. Determine the direction and magnitude of the induced current in the loop if its resistance is 4.50 mΩ.
View Solution
Knowledge Check
An infinitely long cylinder is kept parallel to an uniform magnetic field B directed along positive z-axis. The direction of induced current as seen from the z-axis will be
Aclockwise of the positive z-axisBanticlockwise of the positive z-axisCzeroDalong the magnetic field
The given loop is kept in a uniform magnetic field perpendicular to plane of loop. The field changes from 1000G to 500G in 5 seconds. the average induced emf in loop is
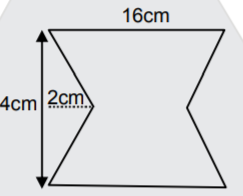 -
-
View SolutionA closed loop with the geometry shown in Fig. 3.9 is placed in a uniform magnetic field direction into the plane of the paper. If the magnetic field decreases with time, determine the direction of the induced emf in this loop.

View SolutionA square loop of side .a. lying in a perpendicular magnetic field to its plane is changed to a circle. If change occurs in .t. seconds in magnetic field B tesla, the induced emf is
View SolutionA square coil of 100 turns and side length 1 cm is rotating in a uniform magnetic field such that axis of rotation is perpendicular to magnetic field. If coil completes 1 rotation in 1ms.Find average EMF induced in μV) in half rotation. ( Magnetic field (B)=10−5T ) .
View SolutionA square coil of 100 turns and side length 1 cm is rotating in a uniform magnetic field such that axis of rotation is perpendicular to magnetic field. If coil completes 1 rotation in 1ms.Find average EMF induced in μV) in half rotation. ( Magnetic field (B)=10−5T ) .
View SolutionA square loop of side 10cm and resistance 0.5Ω is placed vertically in the east-west plane. A uniform magnetic field of 0.10T is set up across the plane in the north-east direction. The magnetic field is decreased to zero in 0.70s at a steady rate. The magnitude of current in this time-interval is.
View SolutionAn infinitely long cylinder is kept parallel to an uniform magnetic field B directed along positive z-axis. The direction of induced current as seen from the z-axis will be
View Solution
