A steel bar 10.0 cm long is welded end to end to a copper bar 20.0 cm long. Both bars are insulated perfectly on their sides . Each bar has a separate cross-section, 2.00 cm on a side . The free end of the steel bar is maintained at 100∘C by placing it in contact with steam and free end of the copper bar is maintained at 0∘C by placing it in contact with ice . find the temperature at the junction of the two bars and the total rate of heat flow . thermal conductivity of steel =50.2Wm−1K−1.thermal conductivity of copper =385Wm−1K−1.
To solve the problem, we will follow these steps:
Step 1: Understand the setup
We have a steel bar and a copper bar welded together. The steel bar is 10 cm long and the copper bar is 20 cm long. The ends of the bars are maintained at different temperatures: the steel bar at 100°C and the copper bar at 0°C. We need to find the temperature at the junction of the two bars and the total rate of heat flow.
Step 2: Identify the given data
- Length of steel bar, Ls=10cm=0.10m
- Length of copper bar, Lc=20cm=0.20m
- Cross-sectional area of each bar, A=(2.00cm)2=0.02m2
- Temperature at the free end of the steel bar, Ts=100°C
- Temperature at the free end of the copper bar, Tc=0°C
- Thermal conductivity of steel, ks=50.2W/m⋅K
- Thermal conductivity of copper, kc=385W/m⋅K
Step 3: Set up the heat flow equations
At steady state, the heat flow through the steel bar equals the heat flow through the copper bar. The heat flow Q through a bar can be expressed using Fourier's law of heat conduction:
Q=k⋅A⋅ΔTL
For the steel bar:
Qs=ks⋅A⋅(Ts−Tj)Ls
For the copper bar:
Qc=kc⋅A⋅(Tj−Tc)Lc
Where Tj is the temperature at the junction.
Step 4: Equate the heat flows
Since Qs=Qc:
ks⋅A⋅(Ts−Tj)Ls=kc⋅A⋅(Tj−Tc)Lc
The area A cancels out:
ks⋅(Ts−Tj)Ls=kc⋅(Tj−Tc)Lc
Step 5: Substitute the known values
Substituting the values:
50.2⋅(100−Tj)0.10=385⋅(Tj−0)0.20
This simplifies to:
502⋅(100−Tj)=1925⋅Tj
Step 6: Solve for Tj
Expanding and rearranging gives:
50200−502Tj=1925Tj
Combining like terms:
50200=1925Tj+502Tj
50200=2427Tj
Tj=502002427≈20.7°C
Step 7: Calculate the total rate of heat flow
Using the calculated junction temperature Tj:
Qs=ks⋅A⋅(Ts−Tj)Ls=50.2⋅0.02⋅(100−20.7)0.10
Calculating:
Qs=50.2⋅0.02⋅79.30.10=79.30.10=796.17W
Final Answers
- Temperature at the junction Tj≈20.7°C
- Total rate of heat flow Q≈796.17W
We have a steel bar and a copper bar welded together. The steel bar is 10 cm long and the copper bar is 20 cm long. The ends of the bars are maintained at different temperatures: the steel bar at 100°C and the copper bar at 0°C. We need to find the temperature at the junction of the two bars and the total rate of heat flow.
- Length of steel bar, Ls=10cm=0.10m
- Length of copper bar, Lc=20cm=0.20m
- Cross-sectional area of each bar, A=(2.00cm)2=0.02m2
- Temperature at the free end of the steel bar, Ts=100°C
- Temperature at the free end of the copper bar, Tc=0°C
- Thermal conductivity of steel, ks=50.2W/m⋅K
- Thermal conductivity of copper, kc=385W/m⋅K
At steady state, the heat flow through the steel bar equals the heat flow through the copper bar. The heat flow Q through a bar can be expressed using Fourier's law of heat conduction:
Q=k⋅A⋅ΔTL
For the steel bar:
Qs=ks⋅A⋅(Ts−Tj)Ls
For the copper bar:
Qc=kc⋅A⋅(Tj−Tc)Lc
Where Tj is the temperature at the junction.
Since Qs=Qc:
ks⋅A⋅(Ts−Tj)Ls=kc⋅A⋅(Tj−Tc)Lc
The area A cancels out:
ks⋅(Ts−Tj)Ls=kc⋅(Tj−Tc)Lc
Substituting the values:
50.2⋅(100−Tj)0.10=385⋅(Tj−0)0.20
This simplifies to:
502⋅(100−Tj)=1925⋅Tj
Expanding and rearranging gives:
50200−502Tj=1925Tj
Combining like terms:
50200=1925Tj+502Tj
50200=2427Tj
Tj=502002427≈20.7°C
Using the calculated junction temperature Tj:
Qs=ks⋅A⋅(Ts−Tj)Ls=50.2⋅0.02⋅(100−20.7)0.10
Calculating:
Qs=50.2⋅0.02⋅79.30.10=79.30.10=796.17W
- Temperature at the junction Tj≈20.7°C
- Total rate of heat flow Q≈796.17W
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.1
10 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.2
10 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
The left end of a copper rod (length=20cm, Area of cross section=0.2cm2) is maintained at 20∘C and the right end is maintained at 80∘C . Neglecting any loss of heat through radiation, find (a) the temperature at a point 11cm from the left end and (b) the heat current through the rod. thermal conductivity of copper =385Wm−1C−1 .
View SolutionA bar of copper of length 75cm and a bar of steel of length 125cm are joined together end to end. Both are of circular cross section with diameter 2cm. The free ends of the copper and the steel bars are maintained at 100∘C and 0∘C respectively. The curved surface of the bars are thermally insulated. What is the temperature of the copper-steel junction? What is the amount of heat transmitted per unit time across the junction? Thermal conductivity of copper is 386Js−1m−1C−1 and that of steel is 46Js−1m−1C−1
View Solution
Knowledge Check
One end of a 0.25 m long metal bar is in steam and the other is in contact with ice . If 12 g of ice melts per minute, what is the thermal conductivity of the metal? Given cross-section of the bar =5×10−4m2 and latent heat of ice is 80calg−1
A20cals−1m−1.∘C−1B10cals−1m−1.∘C−1C40cals−1m−1.∘C−1D80cals−1m−1.∘C−1
What is the temperature of the steel-copper junction in the steady state system show in Fig. 7(e).17? Length of steel rod = 15.0 cm, length of the copper rod = 10.0 cm, temperature of the furnace =300∘C, temperature of other end 0∘C. The are of cross-section of the steel rod is twice that of the copper rod. (Thermal conductivity of steel =50.2js−1m−1K−1 and of copper =3895js−1m−1K−1).

View Solution
The coefficient of thermal conductivity of copper is nine times that of steel. In the composite cylindrical bar shown in Fig. what will be the temperature at the junction of copper and steel ?
View SolutionA uniform copper rod 50 cm long is insulated on the sides, and has its ends exposedto ice and steam,respectively. If there is a layer of water 1 mm thick at each end, calculate the temperature gradient in the bar. The thermal conductivity of copper is 436Wm−1K−1 and that of water is 0.436Wm−1K−1.
View SolutionThree bars of equal lengths and equal area of cross-section are connected in series fig. their thermal conducitives are in the ratio 2:3:4. If at the steady state the open ends of the first and the last bars are at temperature 200∘C and 20∘C respectively, find the temperature of both the junctions.
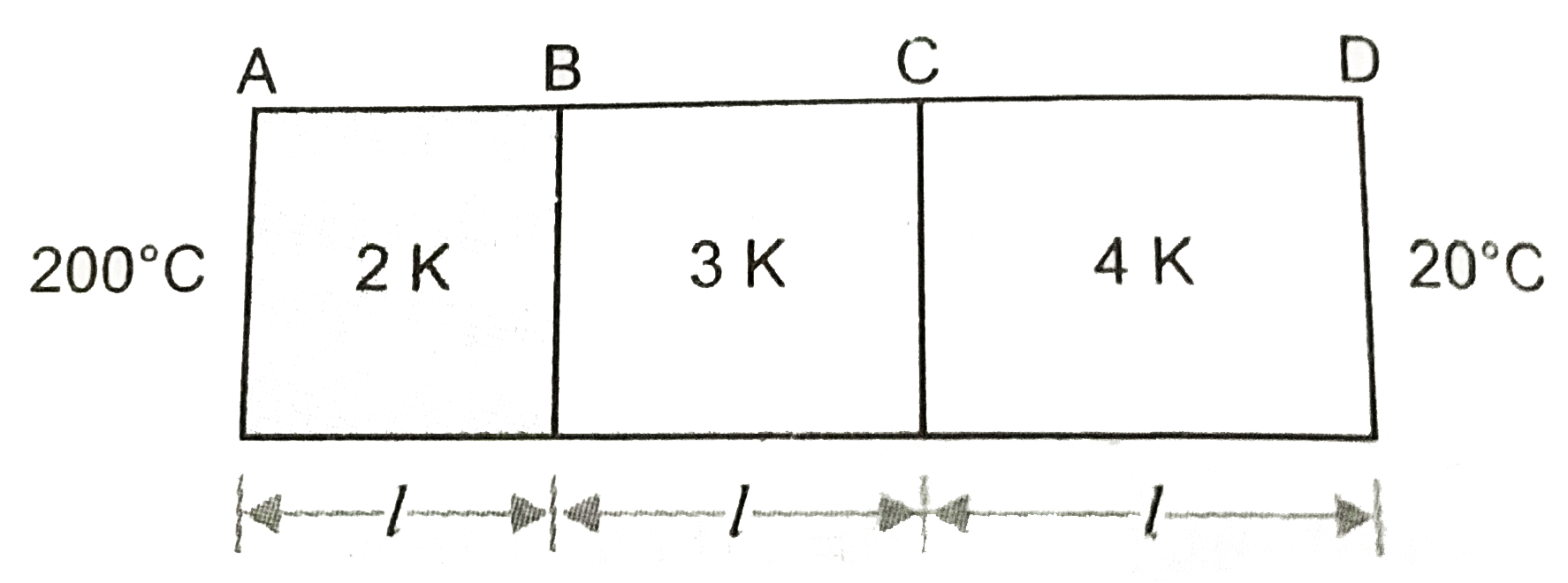 .
.
View SolutionA copper rod of length 75 cm and an iron rod of length 125cm are joined together end to end . Both are of circular cross section with diameter 2 cm . The free ends of the copper and iron are maintained at 100∘C and0∘C respectively . The surface of the bars are insulated thermally . The temperature of the copper -iron junction is [Thermal conductivity of the copper is 386.4W/m−K and that of iron is 48.46W/m−K].
View SolutionA copper strip AB and an iron strip AC are joined at A. The junction A is maintained at 0∘C and the free ends BandC are maintained at 100∘C. There is a potential difference between
View SolutionAn iron needles is attracted to the ends of a bar magnet but not to the middle region of the magnet. Is the material making up the ends of a bar magnet different from that of the middle region?
View Solution
