A steel uniform rod of length 2L cross sectional area A and mass Mis set rotating in a horizontal plane about an axis passing through the centre. If Y is the Young's modulus for steel, find the extension in the length of the rod.Solution in Gujrati
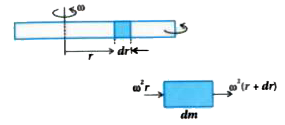
Let us consider an element of width dr at a distance r from the given axis of rotation as showin in the diagram.
Suppose tention in the rod at r and dr distance are T(r)andT(r+dr)
Centripetal force acting on small length element
F=dmrω2 [∵FC=mrω2]
∴F=μrω2dr ...(1)
[∵μ=dmdr⇒dm=μdr]
∴T(r)−T(r+dr)=μrω2dr
[∵T(r)−T(r+dr)= resultant force F]
∴−dT=μrω2dr
Centripetal force and tension force are opposite to each other hence negative sign present.
Integrating on both side.
∫T=0T=TdT=μω2∫lrrdr
−[T]0T=μω2[r22]lr
∴−[0−T]=μω22[l2−r2]
∴T=μω22(l2−r2) ...(2)
Now if Δr is the extension in the elemente of length dr
∴ Young.s modulus Y=T(r)A×drΔr
∴Δrdr=T(r)YA=TYA
∴Δrdr=μω22YA(l2−r2)
∴Δr=μω22YA∫(l2−r2)dr
Integrating on both side,
∫Δr=μω22YA∫(l2−r2)dr
∴Δr=μω22YA[l2r−r33]l0
∴Δr=μω22YA[[l3−l33]
∴Δr=μω22YA×2l33∴Δr=μω2l33YA
∴ Extension of Δr in both side length, then tota extension =2Δr
=2μω2l33YA
Topper's Solved these Questions
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-E
28 Videos
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-F
11 Videos
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-C
66 Videos
- LAW OF MOTIONBOOK - KUMAR PRAKASHANCHAPTER - LAW OF MOTIONEXERCISE - (QUESTION PAPER) SECTION-D
1 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - KUMAR PRAKASHANCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - QUESTION PAPER (SECTION -C)
3 Videos
Similar Questions
Two wires A and B are of the same material their lengths are in the ratio 1 : 2 and the diameter are in the ratio 2 : 1. If they are pulled by the same force, their increase in length will be in the ratio ........
View SolutionTwo wires are made of the same material and have the same volume. The first wire has cross sectional area A and the second wire has cross sectional area 3A. If the length of the first wire is increased by Δl on applying a force F, how much force needed to stretch the second wire by the same amount ?
View SolutionWhat is elasticity ? What is plastic body and plasticity?
View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionGlycerine flows steadily through a horizontal tube of length 1.5m and radius 1.0 cm . If the amount of glycerine collected per second at one is 4.0×10−3kgs−1 , what is the pressure difference between the two ends of the tube ? (Density of glycerine =1.3×10103kgm−3 and viscosity of glycerine =0.83 Pa s). [ you may also like to check if the assumption of laminar flow in the tube is correct]
View SolutionRigidity modulus of steel is eta and its Young's modulus is Y. A piece of steel of cross sectional area A is chaged into a wire of length L and area (A)/(10) then :
View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View SolutionA steel rod of length 2l cross-sectional area A and mass M is set rotating in a horizontal plane about an axis passing through its centre and perpendicular to its length with constant angular velocity ω. If Y is the Young's modulus for steel, find the extension in the length of the rod. (Assume the rod is uniform.)
View SolutionA uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity o in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionA uniform rod of mass m and length l is rotating with constant angular velocity omega about an axis which passes thorugh its one end and perpendicular to the length of rod. The area of cross section of the rod is A and its Young's modulus is y. Neglect gravity. The strain at the mid point of the rod is:
View SolutionA uniform rod of length 2L, area of cross - section A and Young's modulus Y is lying at rest under the action of three forces as shown.
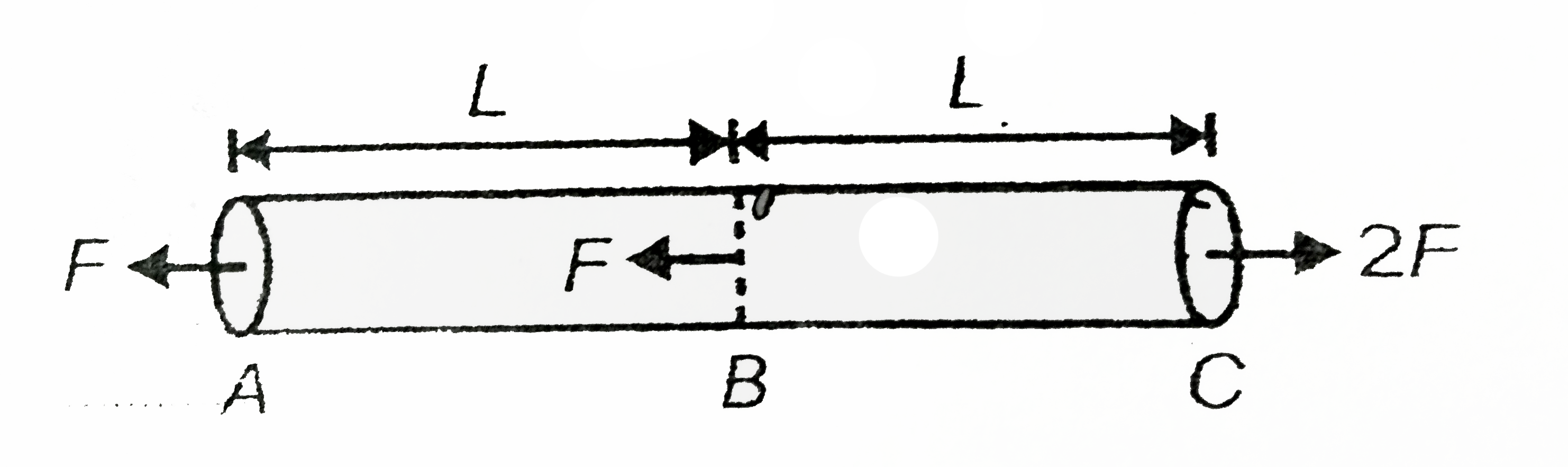
Select the correct alternatives.
View SolutionA uniform rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is omega . Find increase in length of the rod, if rho and Y are the density and Young's modulus of the rod respectively,
View SolutionA steel rod of length L_0 . has a cross sectional area A. The force required to stretch this rod by the same amount as the expansion produced by heating it through DeltaT is (coefficient of linear expansion of steel is alpha and young's modulus for steel is Y ).
View SolutionA stell rod of length 2l corss sectional area A and mass M is set rotating in a horizotnal plane about an axis passing through its cnetre and perpendicular to its length with constant angular velcoty ω. If Y is the Young's modulus for steel, find the extension in the lenght of the rod. (Assume the rod is uniform.)
View Solution
