A stream of a liquid of density p flowin horizontally with speed v rushes out of a tube of radius r and hits a verticla wall nearly normally. Assumi g that the liquid does not rebound from the wall, the force exerted o the wall by the impact of the liquid is given by
πrρv
πrρv2
πr2ρv
πr2ρv2
The correct Answer is:D
To solve the problem of finding the force exerted on the wall by the impact of a liquid stream, we can follow these steps:
1. Identify the Given Parameters:
- Density of the liquid, ρ
- Speed of the liquid, v
- Radius of the tube, r
2. Understand the Flow of Liquid:
- The liquid flows out of the tube horizontally and hits a vertical wall normally (perpendicularly).
- We assume that the liquid does not rebound from the wall.
3. Calculate the Volume Flow Rate:
- The volume flow rate Q of the liquid can be expressed as:
Q=A⋅v
- Where A is the cross-sectional area of the tube. For a circular tube, the area A is given by:
A=πr2
- Therefore, the volume flow rate becomes:
Q=πr2⋅v
4. Calculate the Mass Flow Rate:
- The mass flow rate ˙m can be calculated using the density ρ:
˙m=ρ⋅Q=ρ⋅(πr2⋅v)
5. Determine the Change in Momentum:
- When the liquid hits the wall, it comes to a stop. The change in momentum Δp for the mass flow rate is:
Δp=˙m⋅v=ρ⋅(πr2⋅v)⋅v=ρ⋅πr2⋅v2
6. Calculate the Force Exerted on the Wall:
- The force F exerted on the wall by the impact of the liquid is equal to the rate of change of momentum:
F=Δp=ρ⋅πr2⋅v2
Final Answer:
The force exerted on the wall by the impact of the liquid is given by:
F=πr2ρv2
- Density of the liquid, ρ
- Speed of the liquid, v
- Radius of the tube, r
- The liquid flows out of the tube horizontally and hits a vertical wall normally (perpendicularly).
- We assume that the liquid does not rebound from the wall.
- The volume flow rate Q of the liquid can be expressed as:
Q=A⋅v
- Where A is the cross-sectional area of the tube. For a circular tube, the area A is given by:
A=πr2
- Therefore, the volume flow rate becomes:
Q=πr2⋅v
- The mass flow rate ˙m can be calculated using the density ρ:
˙m=ρ⋅Q=ρ⋅(πr2⋅v)
- When the liquid hits the wall, it comes to a stop. The change in momentum Δp for the mass flow rate is:
Δp=˙m⋅v=ρ⋅(πr2⋅v)⋅v=ρ⋅πr2⋅v2
- The force F exerted on the wall by the impact of the liquid is equal to the rate of change of momentum:
F=Δp=ρ⋅πr2⋅v2
The force exerted on the wall by the impact of the liquid is given by:
F=πr2ρv2
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(NEET)22videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(AIIMS)28videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved Papers 2017(AIIMS)26videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
- BOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions14videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.74videos
SOUND WAVES
Similar Questions
A stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall near by what is the force exerted on the wall by the impact of water assuming.that it does not rebound? (Density of water =1000kgm3)
View SolutionA horizontal jet of water coming out of a pipe of area of cross - section 20 cm2 hits a vertical wall with a velocity of 10 ms−1 and rebounds with the same speed. The force exerted by water on the wall is,
View Solution
Knowledge Check
- Question 1 - Select One
A stream of water flowing horizontally with a speed of 25ms−1 gushes out of a tube of cross-sectional area 10−3m2, and hits at a vertical wall nearby. What is the force exerted on the wall by the impact of water?
A125NB625NC−650ND−1125N - Question 2 - Select One
A stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water assuming that it does not rebound? (Density of water =1000kgm−3)
A1.25×103NB2.25×103NC3.25×103ND4.25×103N
A liquid of density ρ is flowing with a speed V through a pipe of cross sectional area A. What force does the liquid stream exert on wall in x direction if it splashes in the form of a circle after it hits the wall?
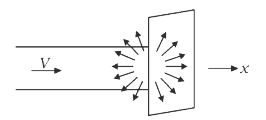 View Solution
View SolutionThe diameter of the top of a firebrigade pump is 5 cm. Water is thrown by this pump at a horizontal speed of 18 m/s on a wall. If water rebounds back from the wall, then the force exerted by water on wall will be :-
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
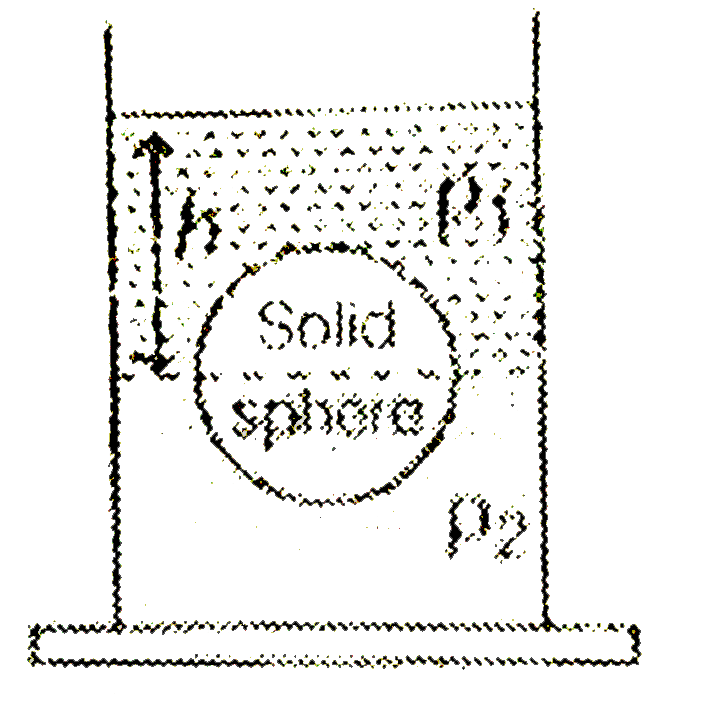 View Solution
View SolutionA large open top container of negligible mass and uniform cross sectional area A a has a small hole of cross sectional area A/100 in its side wall near the bottom. The container is kept on a smooth horizontal floor and contains a liquid of density ρ and mass M0. Assuming that the liquid starts flowing out horizontally through the hole at t=0, calculate a the acceleration of the container and its velocity when 75% of the liquid has drained out.
View Solution_E01_290_Q01.png)
Shown in the figure is a container whose top and bottom diameters are D and d respectively At the bottom of the container these is a cappillary tube of outer radius b and inner radius a. the volume flow rate in the capillary is Q. if the capillary is removed the liquid comes out with a velocity of v0. The density of the liquid is given as calculate the coefficient of viscosity η (given πa2=10−6m2 and a2l=2×10−6m]View SolutionWater from a hosepipe of radius 5 cm strikes a wall at a speed of 5ms−1 normally and stops. The force exerted on the wall in newton is
View Solution

