A body is projected veritclaly upwards.The times corresponding to height h while ascending and while descending are t1 and t2 respectively.
Then, the velocity of projection will be (take g as acceleration due to gravity)
g√t1t22
g(t1+t2)2
g√t1t2
gt1t2(t1+t2)
The correct Answer is:B
To solve the problem, we need to find the initial velocity of a body projected vertically upwards, given the times taken to reach a certain height h during ascent and descent, denoted as t1 and t2 respectively.
1. Understanding the Motion:
- When a body is projected upwards, it moves against the force of gravity until it reaches its maximum height and then descends back down.
- The time taken to reach a height h while ascending is t1, and the time taken to descend back to the same height h is t2.
2. Using the Equation of Motion:
- We can use the second equation of motion:
s=ut+12at2
- Here, s is the displacement (height h), u is the initial velocity (which we denote as u0), a is the acceleration (which is −g when moving upwards), and t is the time.
3. Applying the Equation for Ascent:
- For the ascent to height h:
h=u0t1−12gt21
- Rearranging gives:
2h=2u0t1−gt21
4. Applying the Equation for Descent:
- For the descent from height h:
h=u0t2−12gt22
- Rearranging gives:
2h=2u0t2−gt22
5. Setting Up the Equations:
- We now have two equations:
gt21−2u0t1+2h=0(1)
gt22−2u0t2+2h=0(2)
6. Using the Properties of Quadratic Equations:
- For a quadratic equation ax2+bx+c=0, the sum of the roots t1+t2 is given by −ba.
- Here, a=g, b=−2u0, and c=2h.
- Thus, we can write:
t1+t2=2u0g
7. Solving for Initial Velocity u0:
- Rearranging gives:
u0=g(t1+t2)2
Final Answer:
The velocity of projection u0 is given by:
u0=g(t1+t2)2
- When a body is projected upwards, it moves against the force of gravity until it reaches its maximum height and then descends back down.
- The time taken to reach a height h while ascending is t1, and the time taken to descend back to the same height h is t2.
- We can use the second equation of motion:
s=ut+12at2
- Here, s is the displacement (height h), u is the initial velocity (which we denote as u0), a is the acceleration (which is −g when moving upwards), and t is the time.
- For the ascent to height h:
h=u0t1−12gt21
- Rearranging gives:
2h=2u0t1−gt21
- For the descent from height h:
h=u0t2−12gt22
- Rearranging gives:
2h=2u0t2−gt22
- We now have two equations:
gt21−2u0t1+2h=0(1)
gt22−2u0t2+2h=0(2)
- For a quadratic equation ax2+bx+c=0, the sum of the roots t1+t2 is given by −ba.
- Here, a=g, b=−2u0, and c=2h.
- Thus, we can write:
t1+t2=2u0g
- Rearranging gives:
u0=g(t1+t2)2
The velocity of projection u0 is given by:
u0=g(t1+t2)2
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(NEET)
22 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(AIIMS)
28 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved Papers 2017(AIIMS)
26 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions
The maximum height reached by projectile is 4m. The horizontal range is 12m. The velocity of projection in ms−1 is (g is acceleration due to gravity)
View SolutionA projectile is projected tangentially from the surface of a planet of radius R. If it is at a height of 3R at the farthest point of its trajectory, then the velocity of projection V0 is given by ( acceleration due to gravity on surface=g)
View Solution
Knowledge Check
A particle is projected vertically upwards and it reaches the maximum height H in time T seconds. The height of the particle at any time t will be-
Ag(t−T)2BH−12g(t−T)2C12g(t−T)2DH−g(t−T)2
A ball is projected vertically up such that it passes thorugh a fixed point after a time t1 and t2 respectively. Find
a. The height at which the point is located with respect to the point of projeciton
b. The speed of projection of the ball.
c. The velocity the ball at the time of passing through point P.
d. (i) The maximum height reached by the balll relative to the point of projection A (ii) maximum height reached by the ball relative to point P under consideration.
e. The average speed and average velocity of the ball during the motion from A to P for the time t1 and t2 respectively.
 .
.
View SolutionA stone is projected horizontally with speed v from a height h above ground. A horizontal wind is blowing in direction opposite to velocity of projection and gives the stone a constant horizontal acceleration f( in direction opposite to initial velocity ) .As a result the stone falls on ground at a point vertically below the point of projection. Then the value of height h in terms of f,g,v is (g is acceleration due to gravity 0
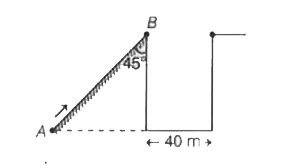
View SolutionA body is projected up a smooth inclined plane of length 20√2m from point A as shown in the figure. The top of B of the inclined plane is connected to a well of diameter 40 m. If the body just manages to cross the well then the velocity of projection is
(Acceleration due to gravity, g=10ms−2)
View SolutionFind the time required for a cylindrical tank of radius r and height H to empty through a round hole of area a at the bottom. The flow through the hole is according to the law v(t)=k√2gh(t) , where v(t) and h(t) , are respectively, the velocity of flow through the hole and the height of the water level above the hole at time t, and g is the acceleration due to gravity.
View SolutionFind the time required for a cylindrical tank of radius r and height H to empty through a round hole of area a at the bottom. The flow through the hole is according to the law v(t)=k√2gh(t) , where v(t) and h(t) , are respectively, the velocity of flow through the hole and the height of the water level above the hole at time t, and g is the acceleration due to gravity.
View SolutionA body is projected vertically upwatds at time t=0 and is it seen at a height H at time t1 and t2 second during its flight. The maximum height attainet is (g is acceleration due to garavity).
View SolutionA particle is projected vertically upwards and reaches the maximum height H in time T. The height of the partlcle at any time t(<T) will be
View Solution
