A stretched string has a mass per unit length of 5.00 g/cm and a tension of 10.0 N A sinusoidal wave on this string has an amplitude of 0.16 mm and a frequency of 100 Hz and is traveling in the negative direction of an x axis. If the wave equation is of the form y(x,t)= ymsin(kx±ωt), what are (a) ym (b) k. (c) ω, and (d) the correct choice of sign in front of ω?
The correct Answer is:(a) 1mm; (b) 141m−1; (c) 628 rad/s; (d) plus sign in used since the wave is traveling in the negative x direction
Topper's Solved these Questions
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Single Correct Choice Type)
33 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (More than One Coorect Choice Type)
10 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Checkpoint
8 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
Similar Questions
Two waves are generated on a string of length 4.0 m to produce a three-loop standing wave with an amplitude of 1.0 cm.The wave speed is 100 m/s. Let the equation for one of the waves be of the form y(x,t)=ymsin(kx+ωt). In the equation for the other wave, what are (a) ym (b) k, (c) ω and (d) the sign in front of w!
View SolutionIn Fig 16-46, a sinusoidal wave moving along a string is shown twice as crest A travels in the positive direction of any x axis by distance d=6.0 cm in 3.0 ms. The tick marks along the axis are separated by 10cm, height H=6.00MM. The equation for the wave is in the form y(x,t) =ymsin(kx±ωt). so what are (a) ym,(b)k,(c)ω and (d) the correct choice of sign in front of ω?
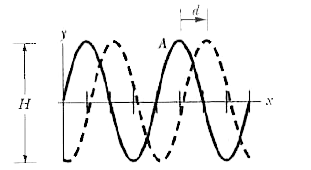
View Solution
Knowledge Check
The tension in a string with a linear density of 0.0010 kg/m iş 0.40 N. A 100 Hz sinusoidal wave on this string has a wavelength of
A0.05cmB2.0cmC5.0cmD20cmA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is
Ay(x,t)=0.5sin(2πx−4πt)By(x,t)=0.5cos(2πx+4πt)Cy(x,t)=0.5sin(πx−2πt)Dy(x,t)=0.5cos(2πx+2πt)A string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
A77m/sB102m/sC110m/sD165m/s
A sinusoidal transverse wave is traveling along a string in the negative direction of an x axis. Figure 16-S1 shows a plot of the displacement as a function of position at time t = 0, the scale of the y axis is set by y = 4.0 cm. The string tension is 3.6 N, and its linear density is 28 g/m. Find the (a) amplitude, (b) wavelength, (e) wave speed, and (d) period of the wave (e) Find the maximum transverse speed of a particle in the string. If the wave is of the form y(x,t)=ymsin(kx±ωt+ϕ), what are (f) k, (g) ω(h)ϕ, and (i) the correct choice of sign in front of ω?

View SolutionA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is [
View SolutionA transverse sinusoidal wave is moving along a string in the opposite direction of an x axis with a speed of 70m/s. At t=0 the string particle at x=0 has a transverse displacement of 4.0 cm and is not moving. The maximum transverse speed of the string particle at x=0 is 16m/s. (a) What is the frequency of the wave? (b) What is the wavelength of the wave? If y(x,t) =ymsin(kx±ωt+ϕ) is the form of the wave equation, what are (c) ym,(d)k,(e)ω(f)ϕ, and (g) the correct of sign in front of ω?
View SolutionA string of total mass 100g & total length 2m is under tension due to the weight of an object of mass 8kg .If the resulting sinusoidal wave in the string has an amplitude of 6cm and frequency 60Hz the power that must be supplied to the string is
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View Solution
