(a) The emf of a cell is E and its intenal resistance is r. Its terminals are connected to a resistance R. The potential difference between the terminal is 12V if R=3Ω and 16V if R=8Ω. Find the values of E and r
(b) When an unknown resistance is connected across a series combination of two identical cells, each of 18V, current through the resistance is 4A. When it is connected across a parallel combination of the same cells, the current through it is 3A. Find the unknown resistance and internal resistance of each cell.
( c) p identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. One cell (X) is joined with reversed polarity. Find the potential difference across each cell except X and also across X.
(d) 12 cells each having the same emf are connected in series and are kept in a closed box. Some of the cells are wrongly connected. This battery is connected in series with an ideal ammeter and two cells of same emf as of 12 cells. The current is 3A when the cells and the battery aid each other and 2A when the cells and battery oppose each other. How many cells in the battery are wrongly connected ?
(a) i=E/(r+R)
p.d. Across cell
VA−VB=V=(E−ir) or iR
V=ERR+r
When R=3Ω,V=12V
R=8Ω,V=16V
12=E×33+r …(i)
16=E×88+r….(ii)
(ii)//(i) ⇒1612=88+r.3+r3
12=3+r8+r⇒8+r=6+2r⇒r=2Ω
12=3E3+r=3E3+2⇒E=20V
(b) Case (a) :
i1=18+18R+2r=36R+2r
4=36R+2r⇒R+2r=9 ...(i)
Case (b) : Two cells of same emf are equivalent to a cell of same emf 18V and resistance r/2
i2=18R+r2
3=18R+r2⇒R+r2=6 ...(ii)
Solving (i) and (ii), r=2Ω,R=5Ω
( c) One cell is wrongly connected
Net emf =(p−2)E
Net resistance =pr
i=(p−2)Epr
All cells are supplying current except X
p.d across each cell (except X)
V=E−ir=E−(p−2)Eprr=E−(p−2)Ep
=2Ep
Cell X is taking current
p.d.V'=E+ir=E+(p−2)Eprr=2(p−1)Ep.
(d) Let n cells are wrongly connected, let emf of each each cell is E and internal resistance is r
New emf of battery =(12−2n)E
Net resistance =12r
(i) When battery and two cells aid each other
Net emf =(12−2n)E+2E
Net resistance =12r+2r=14r
Current i1=(12−2n)E+2E14r=3 ...(i)
(ii) When battery and two cells oppose each other
Net emf =(12−2n)E−2E
Current i2=(12−2n)E−2E14r=2...(ii)
(i)//(ii) ⇒14−2n10−2n=32⇒28−4n=30−6n
2n=2⇒n=1
only one cell is wrongly connected.
(a) 
(b) 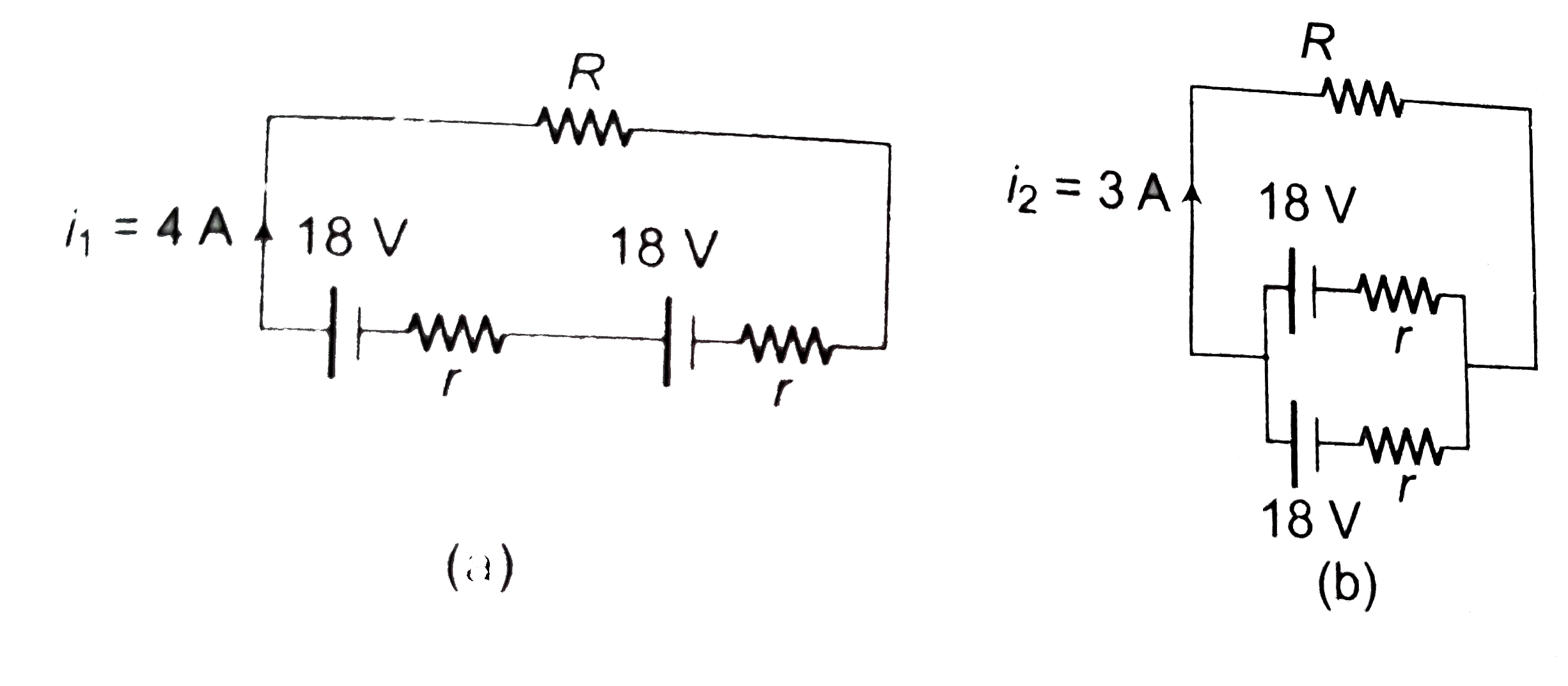

Topper's Solved these Questions
Similar Questions
The emf of a cell is ε and its internal resistance is r. its terminals are connected to a resistance R. The potential difference between the terminals is 1.6V for R=4Ω, and 1.8V for R=9Ω. Then,
View SolutionThe emf of a cell is ε and its internal resistance is r. its termnals are cannected to a resistance R. The potential difference between the terminals is 1.6V for R = 4 Omega, and 1.8 V for R = 9 Omega. Then,
View Solution
Knowledge Check
The emf of a cell is ε and its internal resistance is r. its termnals are cannected to a resistance R. The potential difference between the terminals is 1.6V for R = 4 Omega, and 1.8 V for R = 9 Omega. Then,
Aε=1V,r=1ΩBε=2V,r=1ΩCε=2V,r=2ΩDε=2.5V,r=0.5ΩA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
AEBE/2CE/4D3/2Twenty cells each of emf E and internal resistance r are connected in series to form a loop . If polarity of one of the cell is reserved, then terminal potential across this cell is
A19E10B11E10C9E10DZero
A cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionThe emf of a cell is 2 V. When the terminals of the cell is connected to a resistance 4Ω. The potential difference across the terminals, if internal resistance of cell is 1Ω is
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View Solutionv31
View Solution
