A thick cylindrical shell made of material of thermal conductivity k has inner and outer radii r and R respectively and its length is L. When the curved surface of the cylinder are lagged (i.e., given insulation cover) and one end is maintained at temperature T1 and the other end is maintained at T2(<T1), the heat current along the length of the cylinder is H. In another experiment the two ends are lagged and the inner wall and outer wall are maintained at T1 and T2 respectively. Find the radial heat flow in this case.
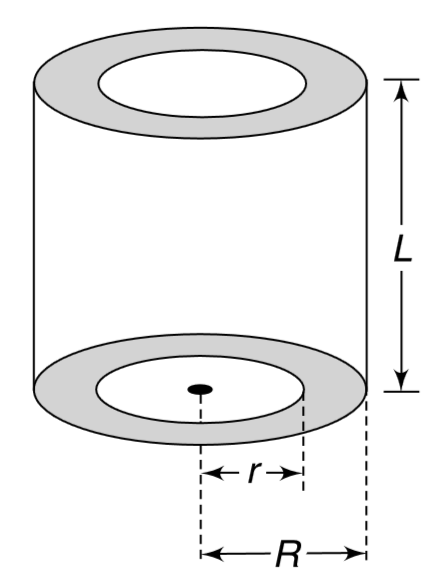
The correct Answer is:2L2HR2−r2ln(Rr)
Step by step video, text & image solution for A thick cylindrical shell made of material of thermal conductivity k has inner and outer radii r and R respectively and its length is L. When the curved surface of the cylinder are lagged (i.e., given insulation cover) and one end is maintained at temperature T_(1) and the other end is maintained at T_(2)(lt T_(1)), the heat current along the length of the cylinder is H. In another experiment the two ends are lagged and the inner wall and outer wall are maintained at T_(1) and T_(2) respectively. Find the radial heat flow in this case. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two lead balls of mass m and 2 m are placed at a separation d. A third ball of mass m is placed at an unknown location on the line joining the first two balls such that the net gravitational force experienced by the first ball is 6Gm2d2 . What is the location of the third ball?
View SolutionA car manufacturer usually tells a optimum speed (V0) at which the car should be driven to get maximum mileage. In order to find the optimum speed for a new model, an engineer of the car company experimented a lot and finally plotted a graph between the extreme time t (defined as number of hours a tank full of petrol lasts) vs the constant speed V at which car was run.
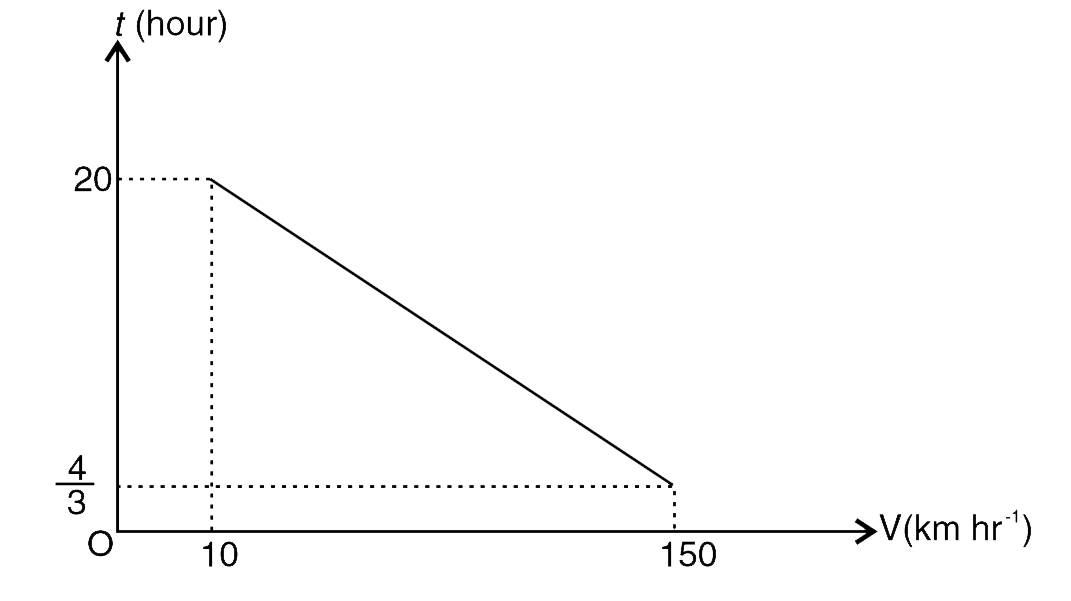
(a) Calculate the optimum speed V0 for this new model.
(b) If the fuel tank capacity of this car is 50 litre, what maximum mileage can be obtained from this car?
View SolutionA hollow tube has a length l, inner radius R1 and outer radius R2 . The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T1 and T2(T_(2)gtT_(1)(b)the∈softhetubeisma∫a∈edattemperatureT_(1)andtheoutsisma∫a∈edatT_(2) .
View Solution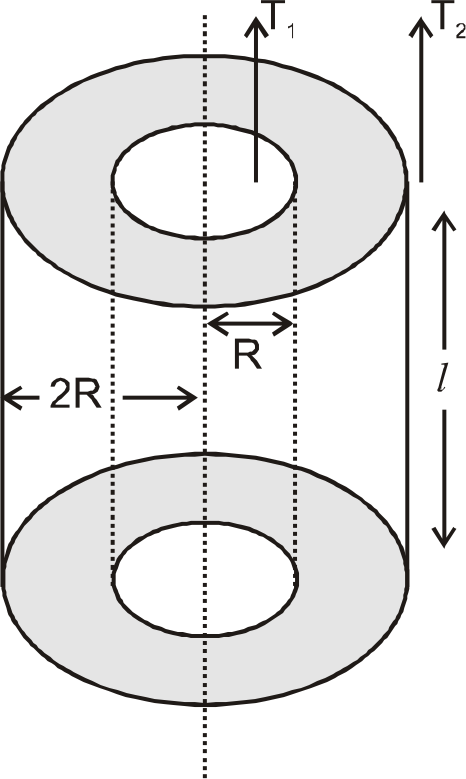
Inner surfaec of a cylindrical shell of length l and of material of thermal conductivity k is kept at constant temperature T1 and outer surface of the cylinder is kept at constant temperature T2 such that (T1>T2) as shown in figure. heat flows from inner surface to outer surface radially outward. inner and outer radii of the shell are R and 2R resspectively. Due to lack of space this cylinder has to be replaced by a smaller cylinder of length l2 inner and outer radii R4 and R respectively and thermal conductivity of material nk. if rate of radially outward heat flow remains same for same temperatures of inner and outer surface i.e., T1 and T2 then find the value of n.
View SolutionA rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
View SolutionA thick spherical shell of inner and outer radii r and R respectively has thermal conductivity k=ρxn , where ρ is a constant and x is distance from the centre of the shell. The inner and outer walls are maintained at temperature T1 and T2(<T1)
(a) Find the value of number n (call it n0) for which the temperature gradient remains constant throughout the thickness of the shell.
(b) For n=n0, find the value of x at which the temperature is T1+T22
(c) For n=n0, calculate the rate of flow of heat through the shell.
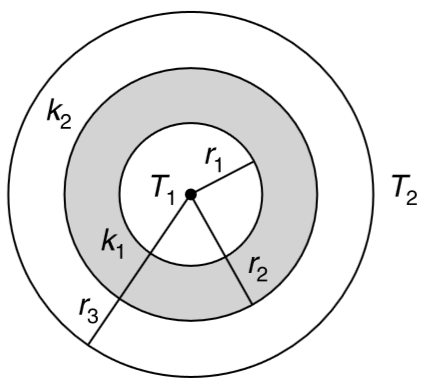
View Solution(i) A cylindrical pipe of length L has inner and outer radii as a and b respectively. The inner surface of the pipe is at a temperature T1 and the outer surface is at a lower temperature of T2. Calculate the radial heat current if conductivity of the mate- rial is K.
(ii) A cylindrical pipe of length L has two layers of material of conduc- tivity K1 and K2. (see figure). If the inner wall of the cylinder is maintained at T1 and outer surface is at T2(<T1), calcu- late the radial rate of heat flow.
View SolutionA tapering rod of length L has cross sectional radii of a and b(lt a) at its two ends. Its thermal conductivity is k. The end with radius a is maintained at a higher temperature T_(1) and the other end is maintained at a lower temperature T_(2) . The curved surface is insulated. (i) At which of the two points – 1 and 2 – shown in the figure will the temperature gradient be higher? (ii) Calculate the thermal resistance of the rod.
View SolutionA cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T0 and the furnace is maintained at T1=T0+ΔT1. The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T2=T0+ΔT2[ΔT2<<T0]. The exposed surface of the rod has emissivity e. Prove that ΔT1 is proportional to ΔT2 and find the proportionality constant.
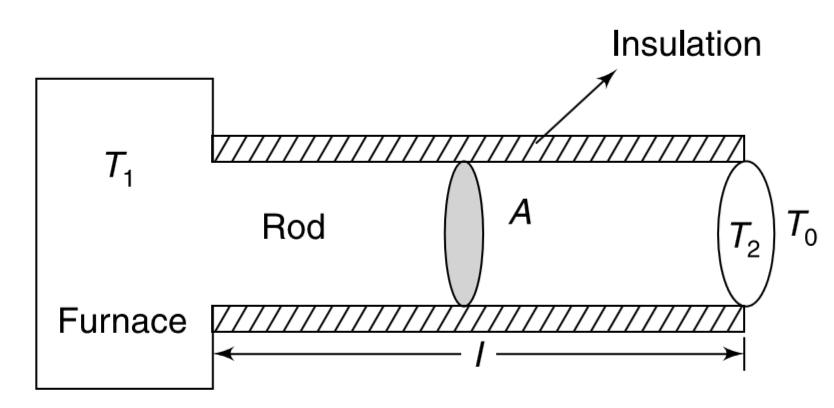
View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = alpha T, where alpha is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T_(1) and T_(2) (T_(1)gtT_(2)) . Heat current flowing through the rod will be
View SolutionA cylinder of radius R is surrounded by a cylindrical shell of inner radius R and oputer radius 2R. The thermal conductivity of the material of the inner cylinder si k_(1) and that of the outer cylinder is K_(2) ,Assumming no loss of heat , the effective thermal conductivity of the system for heat flowing along the length of the cylionder is :
View SolutionThe space between two thin concentric metallic spherical shells of radii a and b is filled with a thermal conducting medium of conductivity k. The inner shell is maintained at temperature T1 and outer is maintained at a lower temperatureT2 . Calculate the rate of flow of heat in radially outward direction through the medium.
View SolutionFind the heat current through the frustum of a cone shown in figure-4.20. Temperature of its two ends are maintained at T1 and T2(T_(2)>T_(1)) respectively and the thermal conductivity of the material is k.
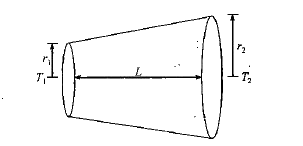
View SolutionA cylinder of radius R made of material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 3R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. What is the effective thermal conductivity of the system ?
View SolutionA slab of material has area A, thickness L, and thermal conducitivy k. One of its surface (P ) is maintained at temperature T1 and the other surface (Q ) is maintained at a lower temperature T2. The rate of heat flow from P to Q is :
View Solution
