A thin film is illuminated by wavelength 600 nm in free space at nearly normal incidence. Calculate the minimum thickness of a thin film (μ = 3/2 ) that results in constructive interference in the reflected light.
To solve the problem of finding the minimum thickness of a thin film that results in constructive interference in the reflected light, we can follow these steps:
Step 1: Understand the Condition for Constructive Interference
For constructive interference in a thin film, the condition is given by the formula:
2μt=(2n+1)λ2
where:
- μ is the refractive index of the thin film,
- t is the thickness of the film,
- λ is the wavelength of light in vacuum,
- n is an integer (0, 1, 2, ...).
Step 2: Substitute the Given Values
We are given:
- Wavelength λ=600nm (or 600×10−9m),
- Refractive index μ=32.
For the minimum thickness, we will take n=0.
Substituting these values into the equation:
2(32)t=(2⋅0+1)600nm2
Step 3: Simplify the Equation
Now, simplify the equation:
2⋅32t=1⋅600nm2
This simplifies to:
3t=300nm
Step 4: Solve for Thickness t
Now, we can solve for t:
t=300nm3
Calculating this gives:
t=100nm
Final Answer
The minimum thickness of the thin film that results in constructive interference in the reflected light is:
t=100nm
---
For constructive interference in a thin film, the condition is given by the formula:
- μ is the refractive index of the thin film,
- t is the thickness of the film,
- λ is the wavelength of light in vacuum,
- n is an integer (0, 1, 2, ...).
We are given:
- Wavelength λ=600nm (or 600×10−9m),
- Refractive index μ=32.
Now, simplify the equation:
Now, we can solve for t:
The minimum thickness of the thin film that results in constructive interference in the reflected light is:
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - EXERCISE (LONG ANSWER QUESTIONS (INTERFERENCE))
4 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - EXERCISE (LONG ANSWER QUESTIONS (DIFFRACTION))
1 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED ) Straight Objective Type Questions)
12 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
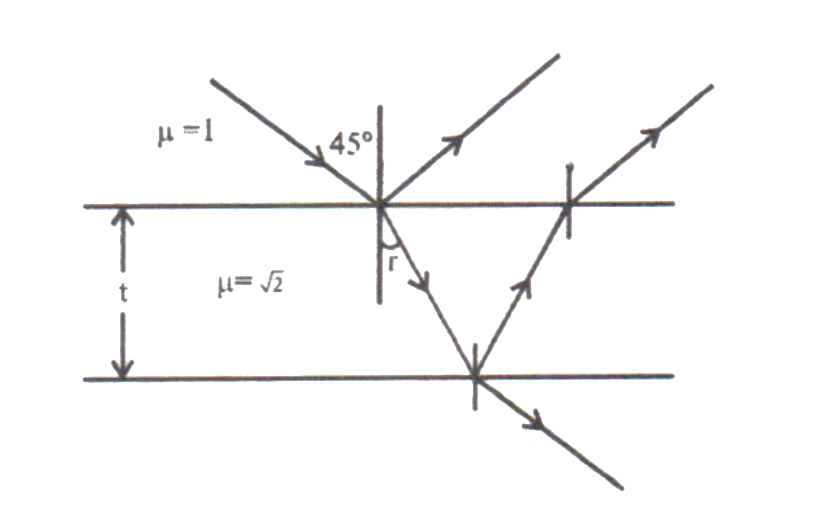
A ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
View SolutionWhat is the minimum thickness of a thin film (μ=1.2) that results in constructive interference in the reflected light? If the film is illuminated with light whose wavelength in free space is λ=500nm ?
View SolutionA light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
View SolutionCalculate the minimum thickness of a soap bubble film (μ=1.33)that results in constructive interference in the reflected light if the film is illuminated with light whose wavelength in free space is λ=600nm.
View SolutionA parallel beam of light of wavelength 560 nm falls on a thin film of oil (refractive index = 1.4). What should be the minimum thickness of the film so that it strongly transmit the light ?
View SolutionAn oil film covers the surface of a small pond. The refractive index of the oil is greater than that of water. At one point on the film, the film has the smallest non-zero thickness for which there will be destructive interference in the reflected light when infrared radiation with wavelength 800 nm is incident normal to the film. When this film is viewed at normal incidence at this same point, for what visible wavelengths, if any, will there be constructive interference? (Visible light has wavelengths between 400nm and 700 nm )
View SolutionA slit of width a is illuminated by monochromatic light of wavelength 650 mm at normal incidence calculate the value of a when
(a). The first minimum falls at an angle of diffraction of 30∘
(b). The first maximum falls at an angle of diffraction of 30∘.
View SolutionA material having an index of refraction of 1.30 is used as an antireflective coating on a piece of glass (n = 1.50). What should be the minimum thickness of this film in order to minimize reflection of 500 nm light?
View SolutionThin films, including soap bubbles and oil show patterns of alternative dark and bright regions resulting from interference among the reflected ligth waves. If two waves are in phase, their crests and troughs will coincide. The interference will be cosntructive and the amlitude of resultant wave will be greater then either of constituent waves. If the two wave are not of phase by half a wavelength (180∘), the crests of one wave will coincide width the troughs of the other wave. The interference will be destructive and the ampliutde of the resultant wave will be less than that of either consituent wave.
1. When incident light I, reaches the surface at point a, some of the ligth is reflected as ray Ra and some is refracted following the path ab to the back of the film.
2. At point b, some of the light is refracted out of the film and part is reflected back through the film along path bc. At point c, some of the light is reflected back into the film and part is reflected out of the film as ray Rc.
Ra and Rc are parallel. However, Rc has travelled the extra distance within the film fo abc. If the angle of incidence is small, then abc is approxmately twice the film's thickness .
If Ra and Rc are in phase, they will undergo constructive interference and the region ac will be bright. If Ra and Rc are out of phase, they will undergo destructive interference and the region ac will be dark.
I. Refraction at an interface never changes the phase of the wave.
II. For reflection at the interfere between two media 1 and 2, if n1>n2, the reflected wave will change phase. If n1<n2, the reflected wave will not undergo a phase change.
For reference, nair=1.00.
III. If the waves are in phase after reflection at all intensities, then the effects of path length in the film are:
Constrictive interference occurs when 2t=mλ/n,m=0,1,2,3,...
Destrcutive interference occurs when 2t=(m+12)λn,
m=0,1,2,3,...
If the waves are 180∘ out of the phase after reflection at all interference, then the effects of path length in the film ara:
Constructive interference occurs when
2t=(m+12)λn,m=0,1,2,3,...
Destructive interference occurs when
2t=mλn,m=0,1,2,3,...
The average human eye sees colors with wavelength between 430 nm to 680 nm. For what visible wavelength (s) will a 350 nm thick (n=1.35) soap film produce maximum destructive interference?
View SolutionA film with index of refraction 1.50 coats a glass lens with index of refraction 1.80. What is the minimum thickness of the thin film that will strongly reflect light with wavelength 600 nm?
View Solution


