A thin rod of length 1m is fixed in a vertical position inside a train, which is moving horizentally with constant acceleration 4ms−2.A bead can slide on the rod and friction coefficient between them is 0.5. If the head is released from rest at the top of the rod , it will reach the bottom the in
√2s
1s
2s
0.5s
The correct Answer is:D
To solve the problem, we need to analyze the forces acting on the bead as it slides down the rod in the accelerating train. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the forces acting on the bead
The bead experiences the following forces:
- Gravitational force (mg) acting downward.
- Normal force (N) acting perpendicular to the rod.
- Frictional force (Ff) acting along the rod, opposing the motion of the bead.
Step 2: Determine the pseudo force
Since the train is accelerating, a pseudo force acts on the bead in the opposite direction of the train's acceleration. The magnitude of this pseudo force is:
Fpseudo=m⋅a
where a=4m/s2 (the acceleration of the train).
Step 3: Calculate the normal force
The normal force N can be equated to the pseudo force acting on the bead:
N=m⋅a=m⋅4
Step 4: Calculate the frictional force
The frictional force Ff is given by:
Ff=μ⋅N=μ⋅(m⋅4)
where μ=0.5 (the coefficient of friction). Thus,
Ff=0.5⋅(m⋅4)=2m
Step 5: Determine the net vertical acceleration
The net vertical acceleration Av of the bead can be expressed as:
Av=g−Ffm
Substituting the values:
Av=g−2=10−2=8m/s2
Step 6: Use kinematic equations to find the time taken to slide down the rod
The bead starts from rest and slides down a distance s=1m with an acceleration Av=8m/s2. Using the kinematic equation:
s=ut+12Avt2
Since the initial velocity u=0:
1=0+12⋅8⋅t2
This simplifies to:
1=4t2
t2=14
t=12s
Conclusion
The time taken for the bead to reach the bottom of the rod is 0.5s.
The bead experiences the following forces:
- Gravitational force (mg) acting downward.
- Normal force (N) acting perpendicular to the rod.
- Frictional force (Ff) acting along the rod, opposing the motion of the bead.
Since the train is accelerating, a pseudo force acts on the bead in the opposite direction of the train's acceleration. The magnitude of this pseudo force is:
Fpseudo=m⋅a
where a=4m/s2 (the acceleration of the train).
The normal force N can be equated to the pseudo force acting on the bead:
N=m⋅a=m⋅4
The frictional force Ff is given by:
Ff=μ⋅N=μ⋅(m⋅4)
where μ=0.5 (the coefficient of friction). Thus,
Ff=0.5⋅(m⋅4)=2m
The net vertical acceleration Av of the bead can be expressed as:
Av=g−Ffm
Substituting the values:
Av=g−2=10−2=8m/s2
The bead starts from rest and slides down a distance s=1m with an acceleration Av=8m/s2. Using the kinematic equation:
s=ut+12Avt2
Since the initial velocity u=0:
1=0+12⋅8⋅t2
This simplifies to:
1=4t2
t2=14
t=12s
The time taken for the bead to reach the bottom of the rod is 0.5s.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Subjective Question
27 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Single Correct
90 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A thin rod of length 1m is fixed in a vertical position inside a train, which is moving horizontally with constant acceleration 4ms−2.A bead can slide on the rod and friction coefficient between them is 0.5. If the bead is released from rest at the top of the rod , it will reach the bottom in
View SolutionThe rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.

View SolutionA long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping is
View SolutionA long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping is
View SolutionIn the arrangement shown in fig., mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion, the ball got opposite to the upper end of the rod. The rod length equals l.
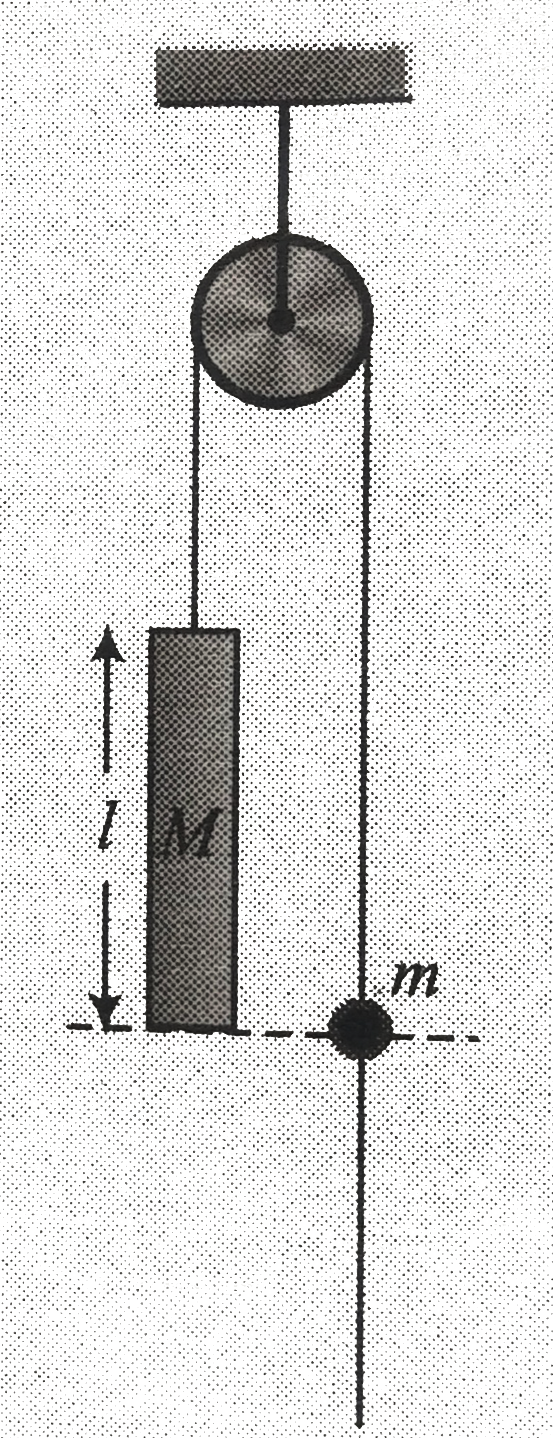
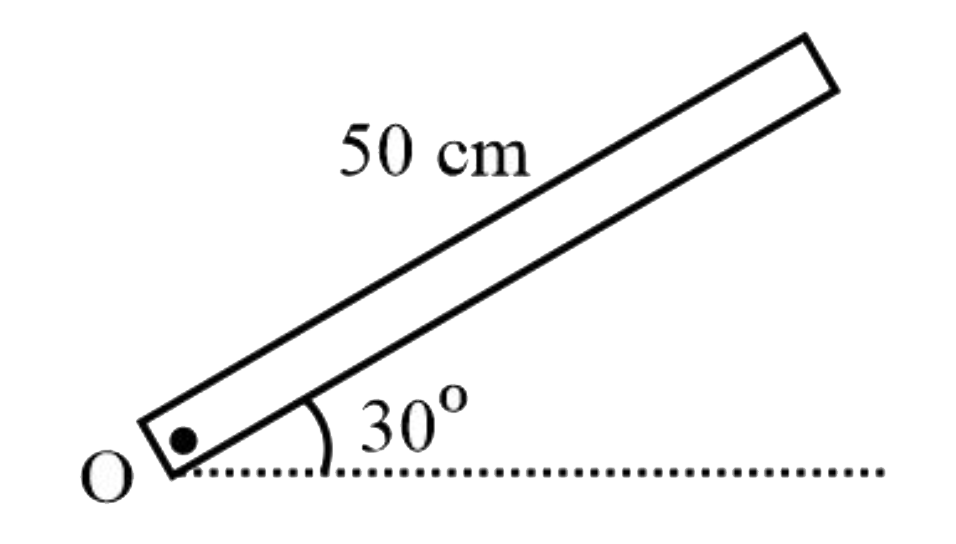
View SolutionA uniform rod of length 50 cm is released in the vertical plane from the position shown in the figure. The rod is hinged smoothly at O. The angular speed of rod when it becomes horizontal is ( take g=10ms−2 )
View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionA thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]

View SolutionOne end of a light spring of natural length 4m and spring constant 170 N/m is fixed on a rigid wall and the other is fixed to a smooth ring of mass 12 kg which can slide without friction in a verical rod fixed at a distance 4 m from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in figure. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
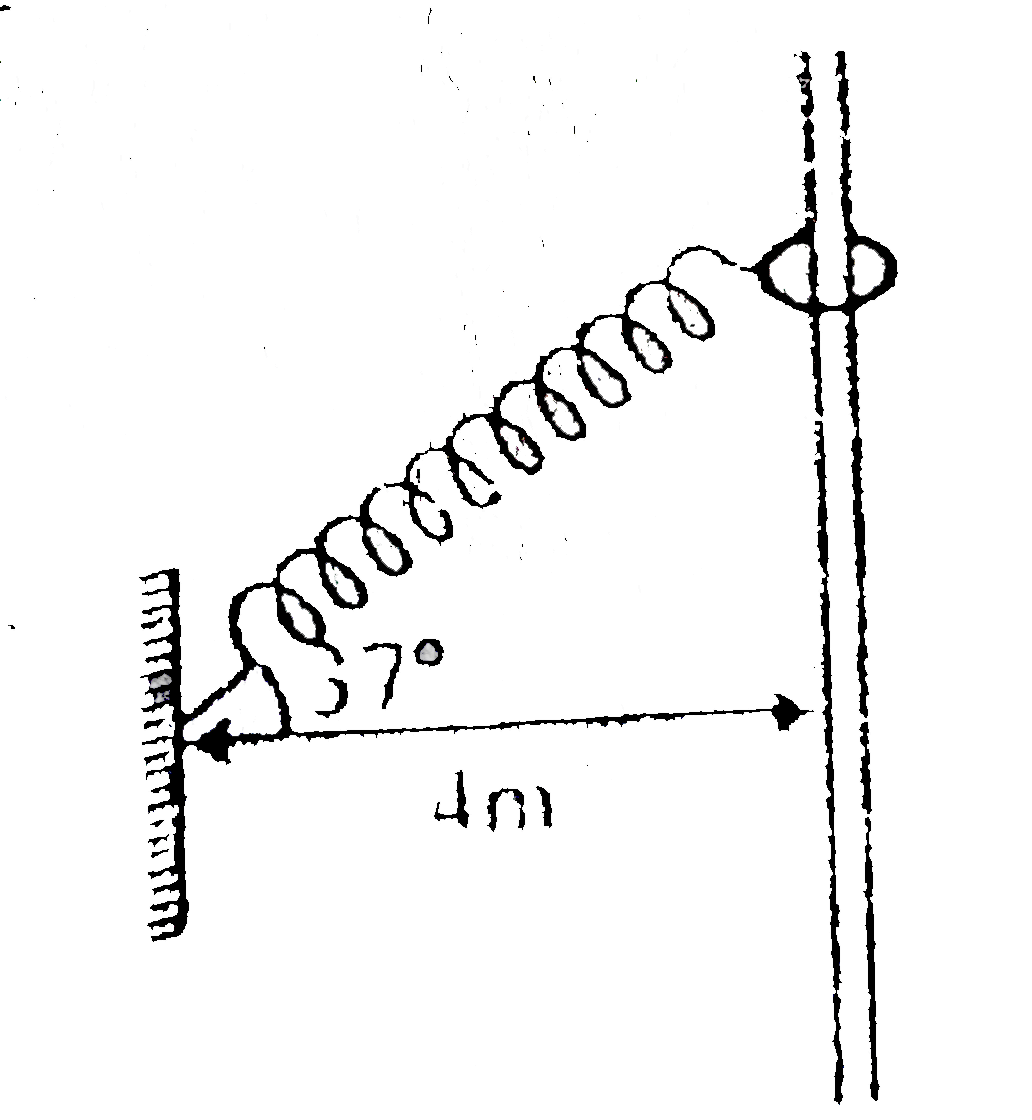
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View Solution
