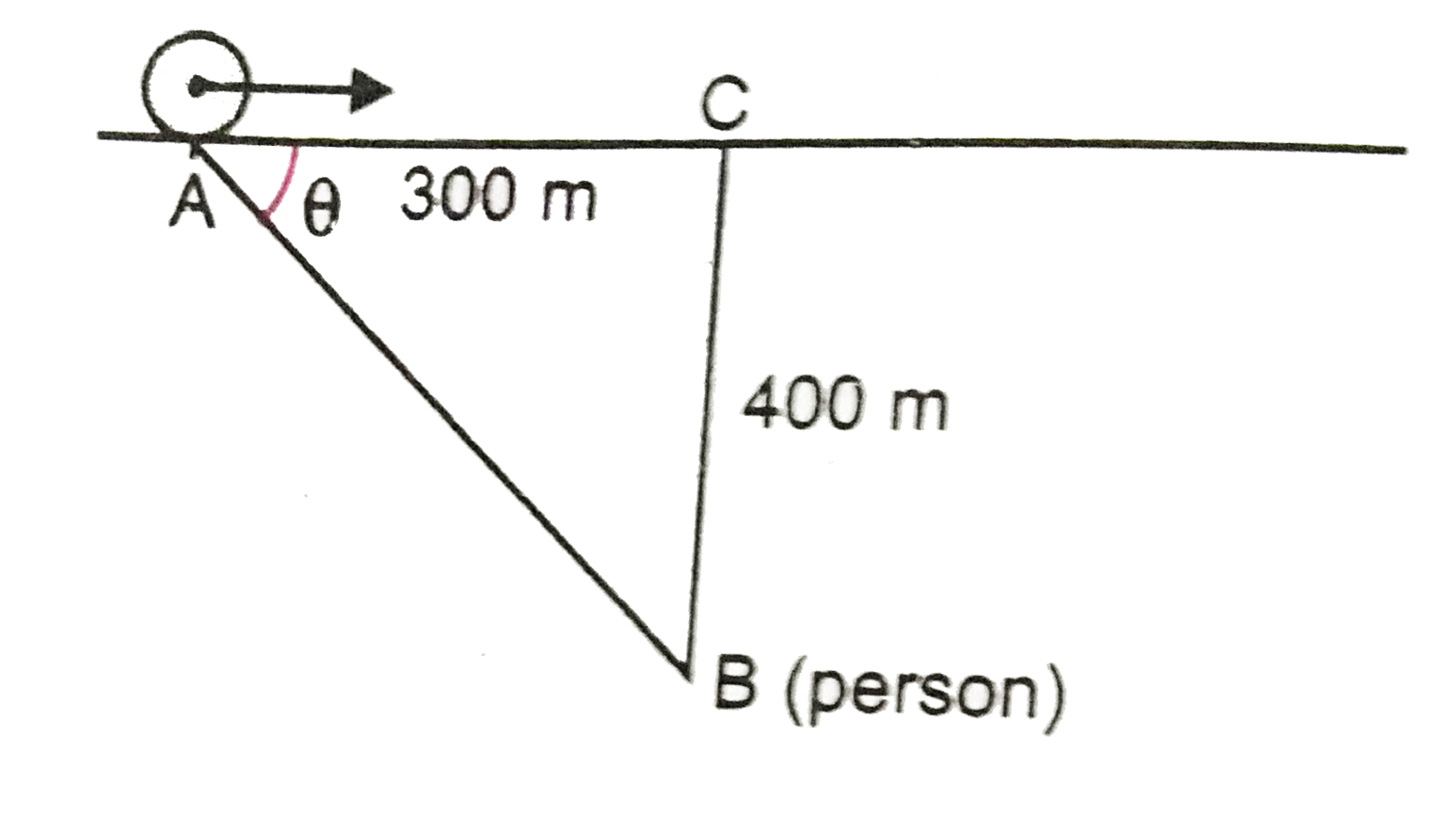
A train approachign a railway crossing at a speed of sounds a short whistle at frequency 640 Hz when it is 300 m away from the crossing. The speed of sound in air is . What will be the frequency heard by a person standing on a road perpendicular to the track through the crossing at a distance of 400 m from the crossing ?
Here,
In figure ,
Let
Component of velocity of source along AB
As the source is approaching the listener, with velocity , therefore apparent frequency,
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - NCERT EXERCISES WITH SOLUTIONS
19 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Additional Exercises
6 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Long Answer Questions
33 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
A train approaching a crossing at a speed of 100 km/h sounds a whistle 400Hz when it is 1.5 km from the crossing. There is no wind and the speed of sound in air is 340 m/s. What frequency is heard by an observer 1.0 km on the strainght road from the crossing at right angles.
View SolutionA locomotive approaching a crossing at a speed of 20 ms−1 sounds a whistle of frequency 640 Hz when 1 km from the crossing. There is no wind and the speed of sound in air is 330 ms−1. What frequency is heard by an observer √3 km on the straight road from the crossing at right angle :-

View Solution
Knowledge Check
A car is approching a railway crossing at a speed of 72kmph. It sounds a horn, when it is 800m away, at 600Hz. If the velocity of sound in air is 330ms−1. The apparent frequency as received by a man at rest near the railway track perpendicular to the road at a distance of 600m from the crossing the
 A653HzB365.5HzC630.5HzD563.5Hz
A653HzB365.5HzC630.5HzD563.5HzA train approaching a railway platform with a speed of 20 m s−1 starts blowing the whistle. Speed of sound in air is 340 ms−1. If the frequency of the emitted sound from the whistle is 640 Hz, the frequency of sound as heard by person standing on the platform
A600 HzB640 HzC680 HzD720 HzAtrain approaching a railway platform with a speed of 20 ms−1 starts blowing the whistle. Speed of sound in air is 340 ms−1 . If the frequency of the emitted sound from the whistle is 640 Hz, the frequency of sound to a person standing on the platform will appear to be
A600 HzB640 HzC680 HzD720 Hz
A locomotive approaching a crossing at a speed of 80 mi/h sounds a whistle of frequency 400 Hz when 1 mi from the crossing. There is no wind, and the speed of sound in air is 0.200mi/s. What frequency is heard by an observer 0.60 mi from the crossing on the straight road which crosses the railroad at right angles?
View SolutionA car approaching a crossing C at a speed of 20m/s sounds a horn of frequency 500HZ when 80m from the crossing . Speed of sound in air is 330m/s . What frequency is heard by an observer (at rest) 60m from the crossing on the straight road which crosses car road at right angles ?
View SolutionA train approaching a hill at a speed of 40km/hr sounds a whistle of frequency 580Hz when it is at a distance of 1km from a hill. A wind with a speed of 40km/hr is blowing in the direction of motion of the train Find
(i) the frequency of the whistle as heard by an observer on the hill,
(ii) the distance from the hill at which the echo from the hill is heard by the driver and its frequency.
(Velocity of sound in air =1,200km/hr)
View SolutionThe speed of sound of a wave having frequency 200 Hz in air is 340 m/s. The speed of sound of wave of frequency 400 Hz in the same air is
View SolutionA source of sound of frequency 600 Hz is placed inside water. The speed of sound in water is 1500m/s and in air it is 300m/s. The frequency of sounds recorded by an observer who is standing in air is :-
View Solution
