A uniform copper bar 100 cm long is insulated on side, and has its ends exposed to ice and steam respectively. If there is a layer of water 0.1 mm thick at each end, calculate the temperature gradient in the bar. KCu=1.04 and Kwater=0.0014 in CGS units.
To solve the problem of finding the temperature gradient in a uniform copper bar with water layers at both ends, we can follow these steps:
Step 1: Understand the Setup
We have a copper bar of length 100 cm, insulated on the sides, with one end exposed to ice (0°C) and the other end exposed to steam (100°C). There are water layers of thickness 0.1 mm at both ends.
Step 2: Convert Units
Convert the thickness of the water layer from mm to cm:
- 0.1 mm = 0.01 cm
Step 3: Calculate Thermal Resistances
We need to calculate the thermal resistance for each layer:
1. Water Layer Resistance (R_water):
Rwater=LK⋅A
For one water layer:
Rwater=0.01cm0.0014cal/cm/s/°C⋅A=0.010.0014A
Since there are two water layers, the total resistance for water is:
Rtotalwater=2⋅Rwater=2⋅0.010.0014A=0.020.0014A
2. Copper Bar Resistance (R_cu):
Rcu=LK⋅A=100cm1.04cal/cm/s/°C⋅A=1001.04A
Step 4: Calculate Total Thermal Resistance
The total thermal resistance Req is the sum of the resistances:
Req=Rtotalwater+Rcu=0.020.0014A+1001.04A
Step 5: Set Up the Temperature Gradient Equation
Using the formula for heat flow:
T2−T1Req=100−0Req
Where T2=100°C and T1=0°C.
Step 6: Calculate the Temperature Gradient
The temperature gradient ∇T can be expressed as:
∇T=T2−T1L=100100=1°C/cm
However, we need to account for the total resistance:
∇T=100Req
Step 7: Substitute and Solve
Substituting Req:
∇T=100(0.020.0014A+1001.04A)
This can be simplified to find the numerical value.
Final Calculation
After performing the calculations, we find:
∇T≈0.87°C/cm
Conclusion
The temperature gradient in the copper bar is approximately 0.87 °C/cm.
---
We have a copper bar of length 100 cm, insulated on the sides, with one end exposed to ice (0°C) and the other end exposed to steam (100°C). There are water layers of thickness 0.1 mm at both ends.
Convert the thickness of the water layer from mm to cm:
- 0.1 mm = 0.01 cm
We need to calculate the thermal resistance for each layer:
1. Water Layer Resistance (R_water):
Rwater=LK⋅A
For one water layer:
Rwater=0.01cm0.0014cal/cm/s/°C⋅A=0.010.0014A
Since there are two water layers, the total resistance for water is:
Rtotalwater=2⋅Rwater=2⋅0.010.0014A=0.020.0014A
Rcu=LK⋅A=100cm1.04cal/cm/s/°C⋅A=1001.04A
The total thermal resistance Req is the sum of the resistances:
Req=Rtotalwater+Rcu=0.020.0014A+1001.04A
Using the formula for heat flow:
T2−T1Req=100−0Req
Where T2=100°C and T1=0°C.
The temperature gradient ∇T can be expressed as:
∇T=T2−T1L=100100=1°C/cm
However, we need to account for the total resistance:
∇T=100Req
Substituting Req:
∇T=100(0.020.0014A+1001.04A)
This can be simplified to find the numerical value.
After performing the calculations, we find:
∇T≈0.87°C/cm
The temperature gradient in the copper bar is approximately 0.87 °C/cm.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Subjective25videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Single Correct148videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Exercise 1.222videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
Similar Questions
A uniform copper rod 50 cm long is insulated on the sides, and has its ends exposed to ice and steam, respectively. If there is a layer of water 1 mm thick at each end, calculate the temperature gradient in the bar. The thermal conductivity of copper is 436Wm−1K−1 and that of water is 0.436Wm−1K−1.
View SolutionA uniform steel rod of length 50 cm is insulated on its sides. There is a layer of water of thick ness 0.2 mm at each end of the rod. If the ends of the rod are exposed to ice at 0∘C, and steam at 100∘C, calculate the temperature gradient in the rod. Thermal conductivities of steel and water are 0.11calcm−1s−1∘C−1and1.5×10−3calcm−1s−1∘C−1
View Solution
Knowledge Check
- Question 1 - Select One
Three rods of Copper, Brass and Steel are welded together to from a Y shaped structure. Area of cross-section of each rod =4cm2. End of copper rod is maintained at 100∘C where as ends of brass and steel are kept at 0∘C. Lengths of the copper, brass and steel rods are 46, 13 and 12 cm respectively. The rods are thermally insulated from surroundings excepts at ends. Thermal cunductivities of copper, brass and steel are 0.92, 0.26 and 0.12 CGS units respectively. Rate of heat flow through copper rod is :
A1.2cal/sB2.4cal/sC4.8cal/sD6.0cal/s
A bar of length 1 m is supported at its two ends. The breadth and depth of the bar are 5 cm and 0.5 cm., respectively , A body of mass 0.1 is suspended at the centre of the bar. Calculate the depression produced in the bar.
View SolutionThe densities of ice and water at 0∘C and 1 bar are 0.96 and 0.99 gm cm−3 respectively. If the percentage of occupied space in ice is x, the the percentage of empty space in water is:
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionA steel bar 10.0 cm long is welded end to end to a copper bae 20.0 cm long. Both bars are insulated perfectly on their sides . Each bar has a separate cross-section, 2.00 cm on a side . The free end of the steel bar is maintained at 100∘C by placing it in contact with ice . find the temperature at the junction of the two bars and the total rate of heat flow . thermal conductivity of steel =50.2Wm−1K−1.thermal conductivity of copper =385Wm−1K−1.
View SolutionA copper rod 2 m long has a circular cross-section of radius 1 cm. One end is kept at 100∘C and the other at 0∘C. The surface is insulated so that negligible heat is lost through the surface. In steady state, find
(a) the thermal resistance of the bar
(b) the thermal current H
(c) the temperature gradient dTdx and
(d) the temperature at a distance 25 cm from the hot end.
Thermal conductivity of copper is 401 W/m−K.View SolutionA steel bar 10.0 cm long is welded end to end to a copper bar 20.0 cm long. Both bars are insulated perfectly on their sides. Each bar has a square cross-section, 20.00 cm on a side. The free end of the steel bar is maintained at 100∘C by placing it in contact with steam, and the free end of the copper bar is maintained at 0∘C by placing it in contact with ice. find the temperature at the junction of the two bars and the total rate of heat flow.
View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the juction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
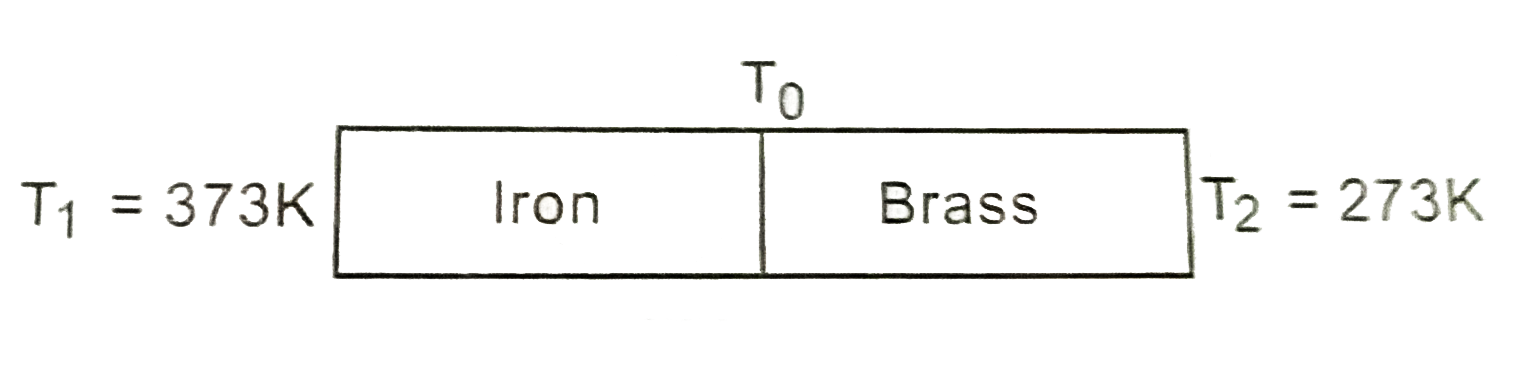 .View Solution
.View Solution

