A uniform cylindrical pulley of mass M and the radius R can freely rotate about the horizontal axis O (figure). The free end of a thread tightly wound on the pulley carries a deadweight A. At a certain angle α it counterbalanes a point mass m fixed at the rim of the pulley. Find the frequency of small osicllations of the arrangement.
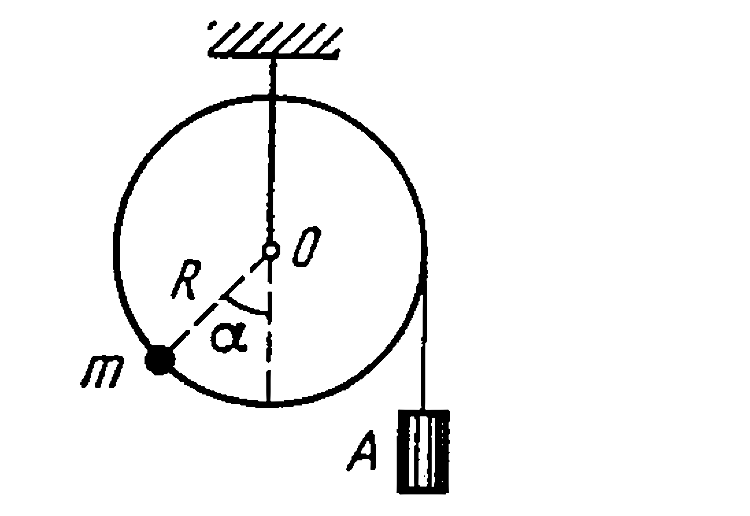
At equillibrium position, Noz=0( Net torque about 0)
So, mAgR−mgRsinα=0or mA=msinα...(1)
From the equation of rotational dynamics of a solid body about the stationary axis ( say z− axis) rotation i.e. from Nz=Iβz
when the pulley is rotated by the small angular displacemetn θ in clockwise sense relative to the equilibrium position (figure) , we get :
mAgR−mgRsin(α+θ)
=[MR22+mR2+mAR2]..θ ltbr> Using Eqn. (1)
mgsinα−mg(sinαcosθ+cosαsinθ)
={MR+2m(1+sinα)R2}..θ
But for small θ , we amy write cosθ≅1 and sinθ≅θ
Thus we have
mgsinα−mg(sinα+cosαθ)={MR+2m(1+sinα)R}2..θ
Hence the sought angular frequency ω0√2mgcosαMR+2mR(1+sinα)

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A uniform solid. cylinder A of mass can freely rotate about a horizontal axis fixed to a mount of mass m2. A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find the acceleration of the point K.
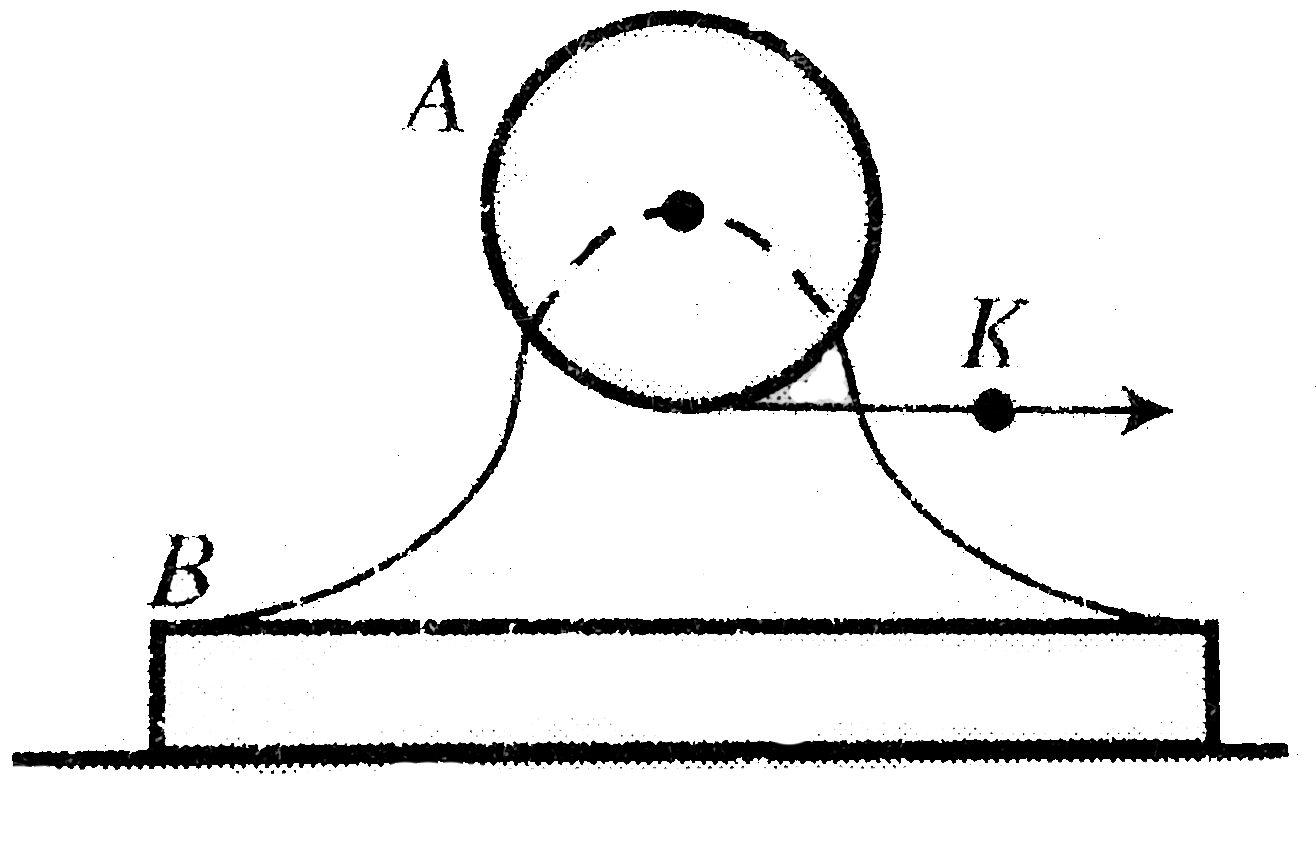
View SolutionA uniform solid cylinder A of mass m1 can freely rotate about a horizontal axis fixed to a mount B of mass m2(figure). A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find:
(a) the acceleration of the point K,
(b) the kinetic energy of this system t seconds after the beginning of motion.

View Solution
Knowledge Check
The semi circular ring of radius R and mass m is free to rotate about the point O in shown figure.
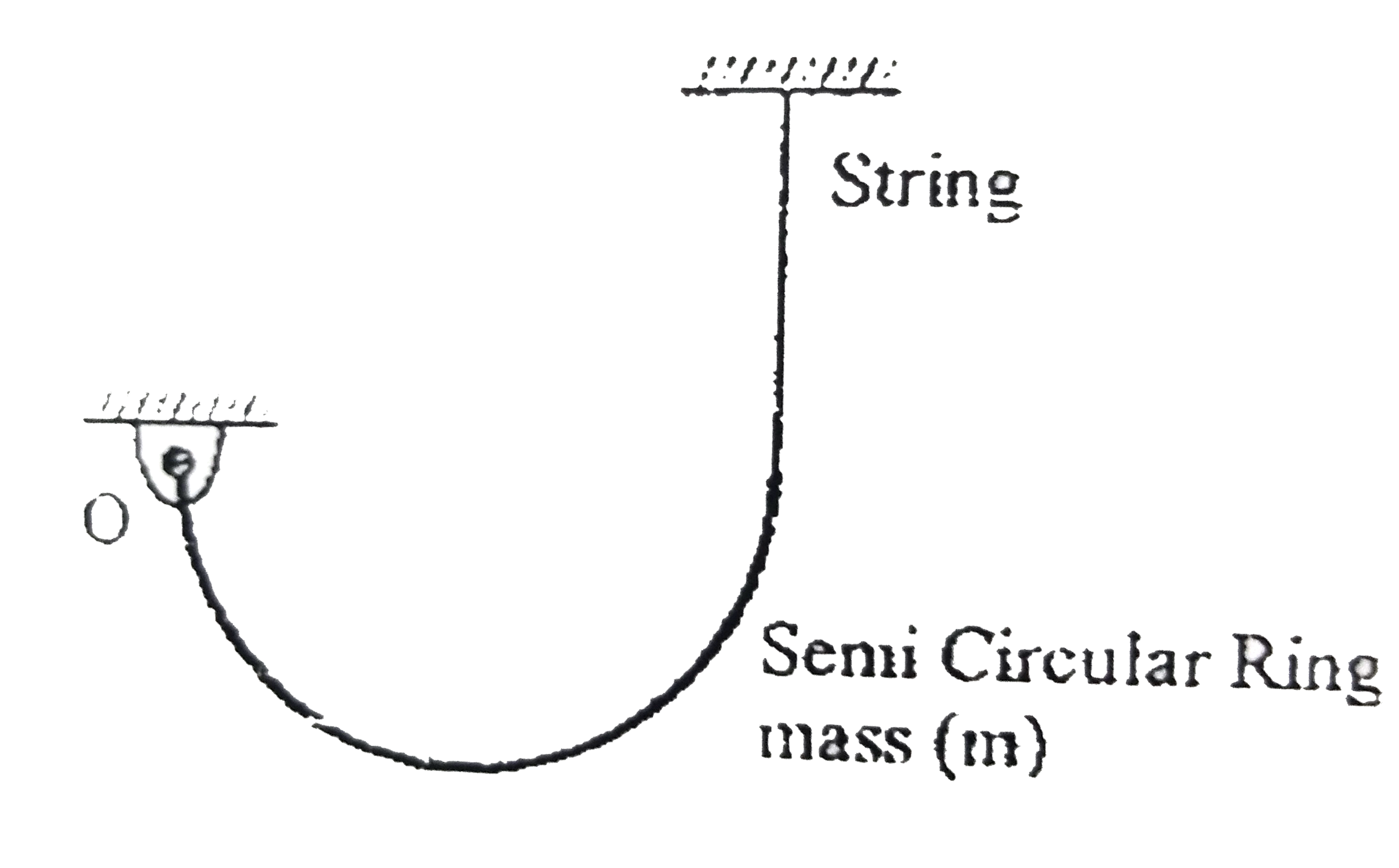 ATension in the string is mg2BAngular acceleration of the semi circular ring just after we cut the string is g4RCForce due to hinge on the semi circular ring always has non zero vetical componentDAcceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal & vertical non zero components.
ATension in the string is mg2BAngular acceleration of the semi circular ring just after we cut the string is g4RCForce due to hinge on the semi circular ring always has non zero vetical componentDAcceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal & vertical non zero components.
A disc of mass M = 2m and radius R is pivoted at its centre. The disc is free to rotate in the vertical plane about its horizontal axis through its centre O. A particle of mass m is stuck on the periphery of the disc. Find the frequency of small oscillations of the system about its equilibrium position.
View SolutionA uniform cylinder of radius R, and mass M rotates freely about a stationary horizontal axix O. A thin cord of length l and mass m is wound on the cylinder in a single layer and its free end is falling vertically. Find the acceleration as a function of the length x of the hanging part of the cord. Assume the center of mass of the wound part of the cord to be the axis of the cylinder.
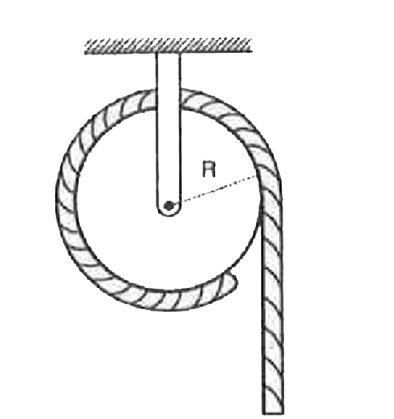
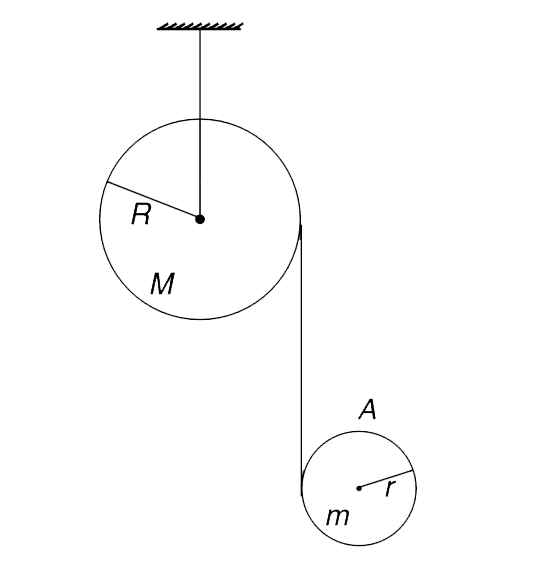
View SolutionA thread is tightly wrapped on two pulleys as shown in figure. Both the pulleys are uniform disc with upper one having mass M and radius R being free to rotate about its central horizontal axis. The lower pulley has mass m and radius r and it is released from rest. It spins and falls down. At the instant of release a small mark (A) was at the top point of the lower pulley.
(a) After what minimum time (t0) the mark will again be at the top of the lower pulley?
(b) Find acceleration of the mark at time t0.
(c) Is there any difference in magnitude of acceleration of the mark and that of a point located on the circumference at diametrically opposite end of the pulley.
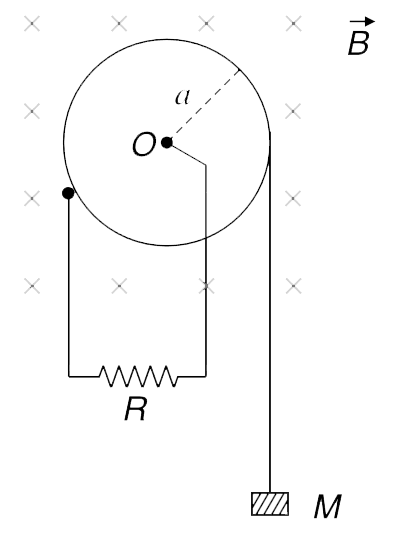
View SolutionA metallic pulley is in the shape of a disc of radius a. It can rotate freely about a horizontal axis passing through its centre. The moment of inertia of the pulley about this axis is I. A light string is tightly wrapped around the pulley with its one end connected to a block of mass M. The centre of the pulley and its circumference are connected to a resistance R as shown. The contact of resistance at the circumference does not cause any friction. A uniform magnetic field B is switched on which is parallel to the axis of rotation of the pulley (see Figure). The mass M is allowed to fall. Assume that resistivity of the material of the pulley is negligible.
(a) Find the acceleration of the block of mass M at the instant its velocity becomes v0.
(b) Assuming that the block can fall through a large distance, calculate the terminal speed (vT) that it will acquire.
(c) Find the rate of change of kinetic energy of the pulley at the instant speed of the falling block is vT2.
View SolutionA uniform spherical shell of mass M and radius R rotates, about a vertical axis on frictionless bearing. A massless cord passes around the equator of the shell., over a pulley of rotational inertia I and radius r and is attached to small object of mass m that is otherwise free to fall under the influence of gravity. There is no friction of pulley's axle, the cord does not slip on the pulley. What is the speed of the object after it has fallen a distance h. from rest? Use work-energy considerations.

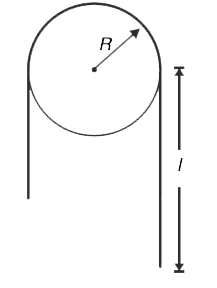
View SolutionA rope of length L and mass per unit length λ passes over a disc shaped pulley of mass M and radius R. The rope hangs on both sides of the pulley and the length of larger hanging part is l. The pulley can rotate about a horizontal axis passing through its centre. The system is released from rest and it begins to move. The pulley has no friction at its axle and the rope has large enough friction to prevent it from slipping on the pulley.
(a) Find the acceleration of the rope immediately after it is released.
(b) Find the horizontal component of the force applied by the axle on the pulley immediately after the system is released
View SolutionA uniform solid cylinder of mass M and radius 2R rests on a horizontal table top. A string attached to it runs over a pulley (disc) of mass M and radius R thatis mounted on a frictionless axle through its centre. A block of mass M is suspended from the free end of the string. The string doesn't slip over the pulley surface, and the cylinder rolls without slipping on the, table top. Find the acceleration of the block.

[g/3]
View Solution
