A Uniform electric field of 10NC−1 exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 50cm.
To solve the problem, we need to find the increase in electric potential when moving upwards through a height of 50 cm in a uniform electric field of 10N/C that is directed downwards.
1. Understand the relationship between electric field and electric potential:
The electric potential difference (ΔV) in a uniform electric field (E) can be calculated using the formula:
ΔV=−E⋅d
where d is the displacement in the direction of the field. The negative sign indicates that potential decreases in the direction of the electric field.
2. Identify the values given in the problem:
- Electric field, E=10N/C
- Height, d=50cm=0.50m (convert cm to m)
3. Substitute the values into the formula:
Since we are moving upwards against the electric field, we will consider d as positive in this case:
ΔV=−E⋅d=−10N/C⋅0.50m
4. Calculate the potential difference:
ΔV=−10⋅0.50=−5V
Since we are moving upwards, the increase in electric potential is:
ΔV=5V
5. Final answer:
The increase in electric potential as one goes up through a height of 50 cm is 5V.
The electric potential difference (ΔV) in a uniform electric field (E) can be calculated using the formula:
ΔV=−E⋅d
where d is the displacement in the direction of the field. The negative sign indicates that potential decreases in the direction of the electric field.
- Electric field, E=10N/C
- Height, d=50cm=0.50m (convert cm to m)
Since we are moving upwards against the electric field, we will consider d as positive in this case:
ΔV=−E⋅d=−10N/C⋅0.50m
ΔV=−10⋅0.50=−5V
Since we are moving upwards, the increase in electric potential is:
ΔV=5V
The increase in electric potential as one goes up through a height of 50 cm is 5V.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - worked out Examples
19 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
A uniform electric field of 20 N/C exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 40 cm.
View SolutionA uniform magnetic field of 0.20×10−3T exists in the space. Find the the change in the magnetic scalar potential as one moves through 50cm along the field.
View SolutionA uniform electric field of magnitude E=100NC−1 exists in the space in x-direction. Calculate the flux of this field through a plane square of edga 10 cm placed in the y-z plane. Take the normal along the positive x-axis to be positive.
View SolutionA particle of mass an charge q is projected vertically upwards .A uniform electric field →E is acted vertically downwards.The most appropriate graph between potential energy U (gravitation plus electrostatic) and height h(<< radius of earth) is :(assume U to be zero on surface of earth)
View SolutionAn electric dipole of length 2 cm is placed with its axis making an angle of 60∘ to a uniform electric field of 105NC−1 if its experiences a torque is 8√3Nm, calculate the
(i). Magnitude of the charge on the dipole and
(ii). potential energy of the dipole.
View SolutionA sphere of mass 50gm is suspended by a string in an electric field of intensity 5NC−1 acting vertically upward. If the tension in the string is 520 milli newton, the charge on the sphere is (g=10ms−2)
View SolutionA sphere of mass 50 gm is suspended by a string in an electric field of intensity 5NC−1 acting vertically upward. If the tension in the string is 520 millinewton, the charge on the sphere is (g=10ms−2)
View SolutionA uniform electric field of strength E exists in region. A electron enters a point A with velocity v as shown. It moves through the electric field and reaches at point B. Velocity particle at B is 2v at 30∘ with x-axis .
Then
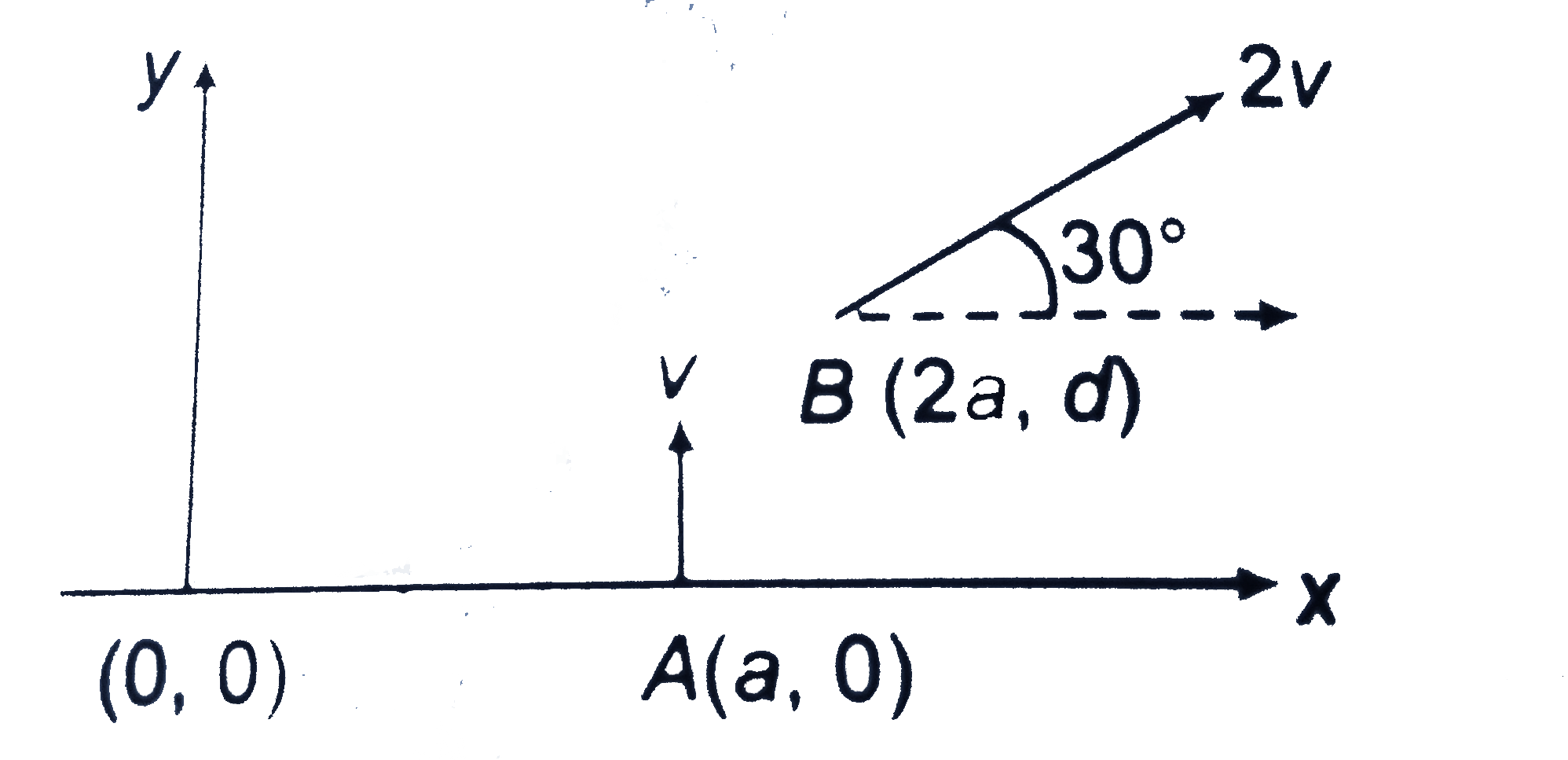
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View Solution
