A uniform frictionless ring of mass M and radius R, stands vertically on the ground. A wall touches the ring on the left and another wall of height R touches the ring on right (see figure).There is a small bead of mass m positioned at the top of the ring. The bead is given a gentle push and it being to slide down the ring as shown. All surfaces are frictionless.

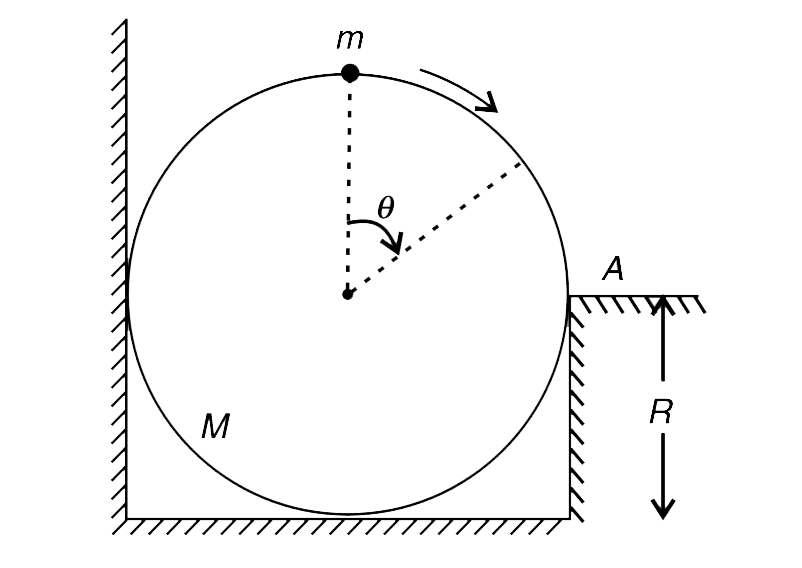
(a) As the bead slides, up to what value of angle $θ$ the force applied by the ground on the ring is larger than Mg?
(b) Write the torque of force applied by the bead on the ring about point A as function of $θ$ .
(c) What is the maximum possible value of torque calculated in (b)? Using this result tell what is the largest value of $\frac{m}{M}$ for which the ring never rises off the ground ?

Text Solution

Verified by Experts

The correct Answer is:(a) $θ = {cos}^{- 1} (\frac{2}{3})$
(b) $m g R (2 cos θ - 3 {cos}^{2} θ)$
(c) $τ_{max} = \frac{m g R}{3}; {(\frac{m}{M})}_{max} = 3$

Updated on:21/07/2023

For a uniform ring of mass M and radius R at its centre
Afield and potential both are zero
Bfield is zero but potential is $\frac{G M}{R}$
Cfield is zero but potential is $- G M / R$
Dmagnitude of field is $\frac{G M}{R^{2}}$ and potential $- \frac{G M}{R}$
Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A $\frac{5}{2} M R^{2}$
B $\frac{3}{2} M R^{2}$
C $\frac{1}{2} M R^{2}$
D $M R^{2}$
Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A $M R^{2}$
B $\frac{1}{2} M R^{2}$
C $\frac{3}{2} M R^{2}$
D $\frac{7}{2} M R^{2}$