A uniform heavy rod of weight W, cross sectional area a and length L is hanging from fixed support. Young modulus of the material of the rod is Y. Neglect the lateral contraction. Find the elongation of the rod.
To find the elongation of a uniform heavy rod of weight W, cross-sectional area A, length L, and Young's modulus Y, we can follow these steps:
Step 1: Understand the Forces Acting on the Rod
The rod is hanging from a fixed support, and its weight W acts downward. The weight creates tension in the rod, which varies along its length.
Step 2: Define the Element of the Rod
Consider an infinitesimal element of the rod at a distance x from the top, with a small length dx. The tension T in this element is due to the weight of the portion of the rod below it.
Step 3: Calculate the Tension in the Element
The weight of the rod below the element at position x is given by:
T=WL⋅(L−x)
This expression represents the weight of the rod below the element, where WL is the weight per unit length.
Step 4: Apply Young's Modulus
Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain
Where:
- Stress σ=TA
- Strain ϵ=ΔLL
For our infinitesimal element, the elongation dΔL can be expressed as:
dΔL=T⋅dxA⋅Y
Step 5: Substitute the Expression for Tension
Substituting the expression for T into the elongation equation:
dΔL=(WL⋅(L−x))⋅dxA⋅Y
Step 6: Integrate to Find Total Elongation
To find the total elongation ΔL of the rod, integrate dΔL from x=0 to x=L:
ΔL=∫L0WL⋅A⋅Y(L−x)dx
Step 7: Solve the Integral
The integral can be solved as follows:
ΔL=WL⋅A⋅Y∫L0(L−x)dx
Calculating the integral:
∫L0(L−x)dx=(Lx−x22)L0=(L2−L22)=L22
Thus,
ΔL=WL⋅A⋅Y⋅L22
Step 8: Simplify the Expression
Finally, simplifying gives:
ΔL=WL2AY
Final Answer
The elongation of the rod is:
ΔL=WL2AY
---
The rod is hanging from a fixed support, and its weight W acts downward. The weight creates tension in the rod, which varies along its length.
Consider an infinitesimal element of the rod at a distance x from the top, with a small length dx. The tension T in this element is due to the weight of the portion of the rod below it.
The weight of the rod below the element at position x is given by:
T=WL⋅(L−x)
This expression represents the weight of the rod below the element, where WL is the weight per unit length.
Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain
Where:
- Stress σ=TA
- Strain ϵ=ΔLL
dΔL=T⋅dxA⋅Y
Substituting the expression for T into the elongation equation:
dΔL=(WL⋅(L−x))⋅dxA⋅Y
To find the total elongation ΔL of the rod, integrate dΔL from x=0 to x=L:
ΔL=∫L0WL⋅A⋅Y(L−x)dx
The integral can be solved as follows:
ΔL=WL⋅A⋅Y∫L0(L−x)dx
Calculating the integral:
∫L0(L−x)dx=(Lx−x22)L0=(L2−L22)=L22
Thus,
ΔL=WL⋅A⋅Y⋅L22
Finally, simplifying gives:
ΔL=WL2AY
The elongation of the rod is:
ΔL=WL2AY
Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Short Answer
18 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective 1
29 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- SOUND WAVESBOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Exercises
89 Videos
Similar Questions
A uniform heavy rod of weight 10 kg ms−2, cross-sectional area 100 cm2 and length 20 cm is hanging from a fixed support. Young modulus of the material of the rod is 2×1011Nm−2 Neglecting the lateral contraction, find the elongation of rod due to its own weight:
View SolutionA rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
View Solution
Knowledge Check
A unifrom steel rod of length 1m and area of cross-section 20cm2 is hanging from a fixed support. Find the increases in the length of the rod.
A1.923×10−5cmB2.923×10−5cmC1.123×10−5cmD3.123×10−5cmA uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
A12ρgLB14ρgLCρgLDNone of theseA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKL
" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionA uniform rod of length 2L, area of cross - section A and Young's modulus Y is lying at rest under the action of three forces as shown.
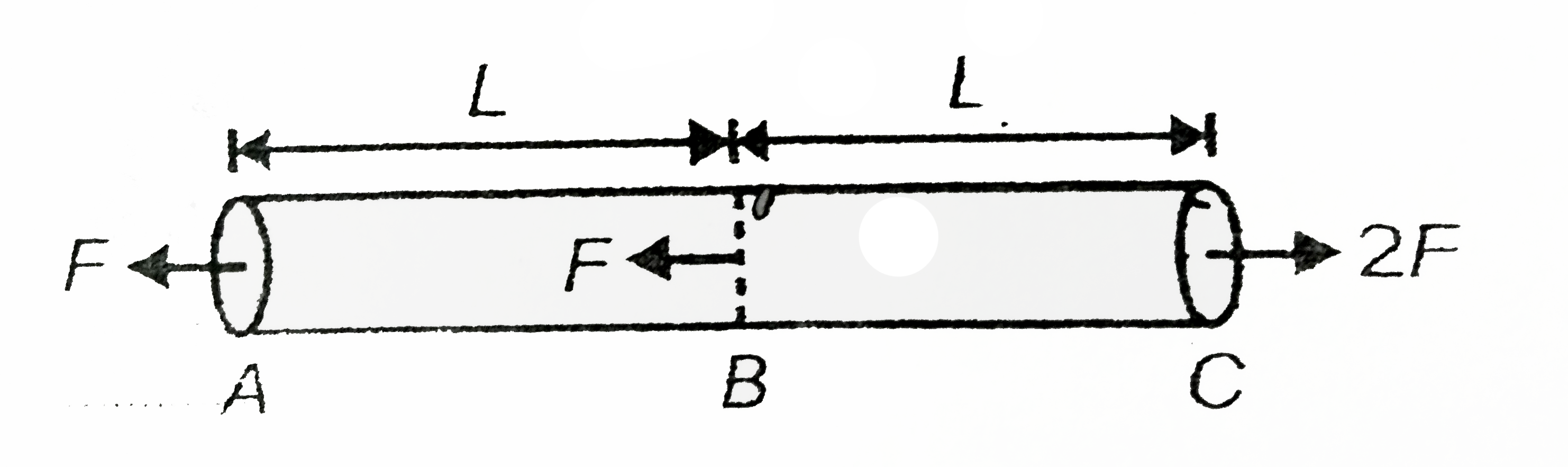
Select the correct alternatives.
View SolutionA uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.

The elongation produced in the rod is
View SolutionA metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y, then the work done is proportional to
View SolutionA metallic rod of length l and cross - sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y, then the work done is proportional to
View Solution
