Question

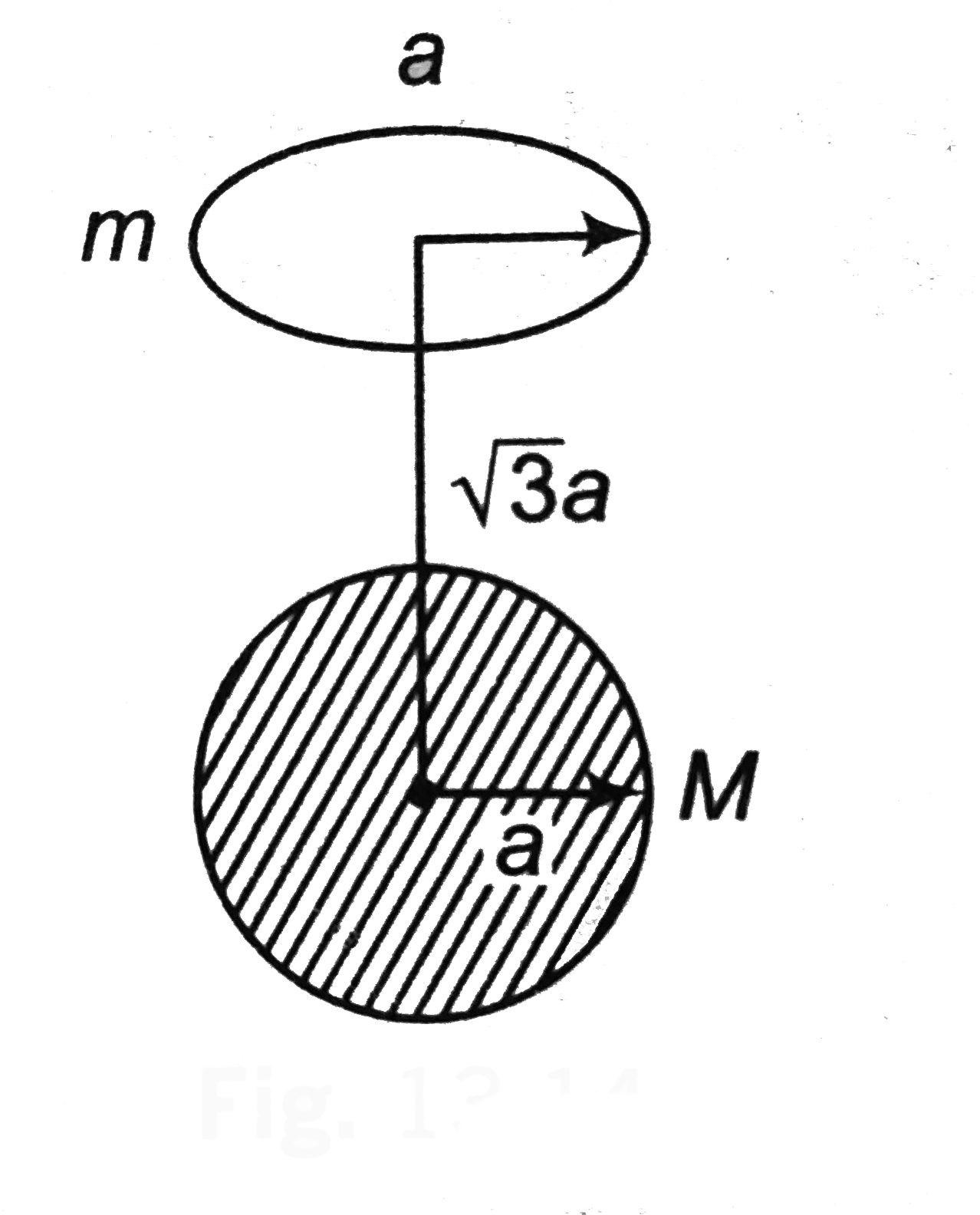
A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance $\sqrt{3}a$ from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.

Explanation

To find the gravitational force exerted by the sphere on the ring, we can follow these steps:

Step 1: Understand the Configuration
We have a uniform ring of mass \( m \) and radius \( a \) positioned directly above a uniform sphere of mass \( M \) and radius \( a \). The distance between the center of the ring and the center of the sphere is given as \( \sqrt{3}a \).

Step 2: Treat the Sphere as a Point Mass
For the purpose of calculating the gravitational force, we can treat the uniform sphere as a point mass located at its center. This is valid because the gravitational force exerted by a uniform sphere can be treated as if all its mass were concentrated at its center.

Step 3: Calculate the Gravitational Field Due to the Ring
The gravitational field \( E \) at a distance \( r \) from the center of the ring can be expressed as:
\( E = \frac{GM}{a^2 + r^2} \cdot \frac{r}{(a^2 + r^2)^{3/2}} \)
where \( G \) is the gravitational constant, \( M \) is the mass of the sphere, \( a \) is the radius of the ring, and \( r \) is the distance from the center of the ring to the center of the sphere.

Step 4: Substitute the Values
In our case, \( r = \sqrt{3}a \) and \( a = a \). Thus, we substitute these values into the equation:
\( E = \frac{GM}{a^2 + (\sqrt{3}a)^2} \cdot \frac{\sqrt{3}a}{(a^2 + 3a^2)^{3/2}} \)
This simplifies to:
\( E = \frac{GM}{4a^2} \cdot \frac{\sqrt{3}a}{(4a^2)^{3/2}} \)

Step 5: Simplify the Expression
Now we simplify the expression:
\( E = \frac{GM \cdot \sqrt{3}a}{4a^2 \cdot 8a^3} = \frac{\sqrt{3}GM}{32a^2} \)

Step 6: Calculate the Gravitational Force
The gravitational force \( F \) exerted by the sphere on the ring can be calculated using the formula:
\( F = m \cdot E \)
Substituting the expression for \( E \):
\( F = m \cdot \frac{\sqrt{3}GM}{32a^2} \)

Final Answer
Thus, the gravitational force exerted by the sphere on the ring is:
\( F = \frac{\sqrt{3}GmM}{32a^2} \)